附加多个集中质量加筋板的自由振动分析

李凯，何书韬，邱永康，吴国民，郭文杰，李天匀

附加多个集中质量加筋板的自由振动分析

李凯1，何书韬1，邱永康2，吴国民1，郭文杰2，李天匀2

1中国舰船研究设计中心，湖北武汉430064
2华中科技大学船舶与海洋工程学院，湖北武汉430074

基于能量泛函变分的方法，研究附加多个集中质量纵横加筋板的自由振动特性。在处理板与筋条的变形协调约束条件时，通过引入拉格朗日乘子，把板、梁组合振动分析问题转化为处理一类无约束泛函变分问题，从而得到加筋板的广义特征值矩阵方程。通过集中质量点的形式引入板上装载设备质量。求解方程可以得到组合结构的各阶固有频率。以四边简支边界条件纵横离散加筋板为计算实例，通过特征值确定其振型并与仿真分析结果进行对比分析，表明其准确有效，可为此类工程问题的研究提供理论基础。

加筋板；集中质量；拉格朗日乘子；泛函变分

期刊网址：www.ship-research.com

引用格式：李凯，何书韬，邱永康，等.附加多个集中质量加筋板的自由振动分析［J］.中国舰船研究，2015，10（5）：66-70.

LIKai，HE Shutao，QIU Yongkang，et al.Free vibration analysisof rectangular stiffened plateswith several lumped mass［J］.Chinese Journalof Ship Research，2015，10（5）：66-70.

0　引言

装载设备的加筋板结构在现代船舶工程结构中占据着重要地位，对附加多个集中质量纵横离散加筋板的自由振动的研究不仅可以精确预报出其固有频率、振型和感兴趣部位的内力矩，在实际工程中起到防止结构发生共振出现有害振动的作用，而且对结构动力分析具有重要的理论意义。

由于加筋板结构的广泛应用，其动态特性求解方法得到国内外学者的大量研究。Chen等［1］通过使用有限差分法研究了具有单筋的矩形加筋板的自由振动特性。在能量方程中出现的导数由有限差分方程组取代，能量方程根据相对离散的位移分量、自然频率和加筋板的振型进行最小化，其中振型可以通过特定的线性代数特征值问题进行解决。Dowell［2］提出采用拉格朗日乘子法对任意边界条件的线性结构进行自由振动分析，该方法基于运用拉格朗日算子代换瑞利—李兹法分析结构模态时的该结构的边界或约束条件。Azimi等［3］利用导纳法对在两对边简支和/或固定，另外两对边刚性简支和简支的边界条件下的矩形薄板进行计算，求解了类似的问题。Aksu等［4］基于变分原理与有限差分法相结合的方法求解了偏心加筋板的动态特性，分析考虑了板的面内变形的方向和面内惯性。板和加强筋的应变能与动能运用有限差分方法由离散的位移分量表示。Mead等［5］采用用于研究二维周期结构的波传播方法对常规的正交阵列均匀梁钢筋进行了研究。Bishop等［6］通过动柔度法对组合结构的动态分析进行了研究。Godfracht等［7］利用伽辽金法在充分考虑板和加强筋之间结合处的转角协调等因素后，对此类问题进行了分析。曾子平等［8］应用拉格朗日乘子法，通过引入拉格朗日乘子，将板、梁组合结构的振动分析问题处理成了一类无约束泛函变分问题，通过建立组合结构的广义特征值问题来求解此类问题。Mukherjee等［9］等通过引入一个等参加筋板单元解决了偏心加筋板的自由振动问题，该单元具有适应不规则边界的能力。此外，该方法因考虑了剪切变形，因而适用于厚板和薄板。Qing等［10］基于状态向量方程理论的半解析法，即一种将复合材料加筋板的板和加强筋单独考虑的新的自由振动分析的数学模型，考虑对复合材料加筋板的板和加强筋单独开发。

本文将首先考虑板与加强筋在特定边界条件下的振动特性，通过引入拉格朗日乘子，将离散加筋板的结构动力学分析问题转化为能量泛函变分问题进行处理，以能量法为基础构建其广义特征值问题，通过集中质量点的形式对附加设备进行处理，以推导加筋板组合结构的相关公式。与Dowell［2］的方法相比，本文并不涉及求解非线性特征值问题，避免了搜根的奇异性难题。本文将求解四边简支附加多个集中质量的加筋矩形板的前五阶固有频率，并与有限元仿真结果进行对比分析，以说明本方法的有效性。

1　理论分析

本文的研究对象是一边长分别为a，b，厚度为h的加筋矩形薄板，将装载设备质量以集中质量点的形式布置在板上。坐标系选取和加强筋的分布如图1所示。其中：横向加筋数为imax，间距为b/（imax+1）；纵 向 加 筋 数为jmax，间距 为a/（jmax+1）；黑点表示集中质量。

薄板弯曲自由振动满足

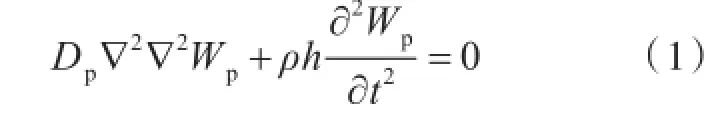
式中：∇2为拉普拉斯算子，；，为弯曲刚度；Wp为薄板挠度函数；μ为板的泊松比。

等截面梁（筋）的自由弯曲振动微分方程为

式中：E为弹性模量；I为截面惯量矩；ρ为梁单位长度的质量；Wb为梁的挠度函数。

图1　加筋薄板模型Fig.1　Modelof the stiffened platemodel

根据船舶结构的特点，不失一般性，假设加筋板的边界为简支，则加强筋可看作两端简支梁，由此，板的挠度、第i根横向筋条的挠度及第 j根纵向筋条的挠度可以分别表示为：

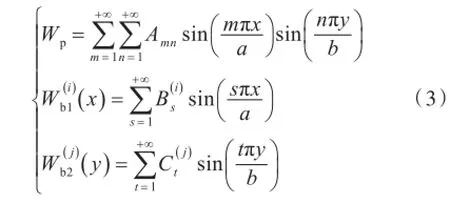
式中：Wp为板的挠度函数；W（）ib1为横向加强筋的挠度函数，为纵向加强筋的挠度函数；Amn为板的幅值；为横向加强筋的幅值，为纵向加强筋的幅值；m和n为板振型沿坐标方向的半波数。

加强筋与板组合应满足位移连续条件，在板与加筋条结合处位移相同，故其满足变形协调条件：

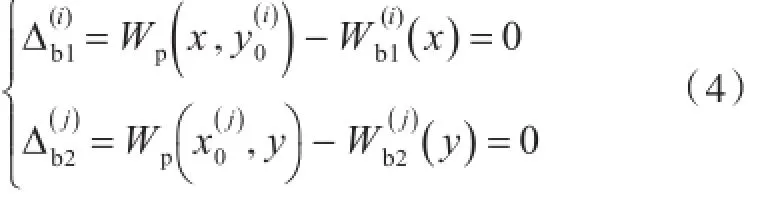
对本文研究对象而言，纵、横加强筋的边界条件与板在该边上的边界条件一致，即梁的两端简支。所以梁和板结合部的振型可以用梁的振型表示：

式中，S为截断项数。

将上式进行正交化处理，得

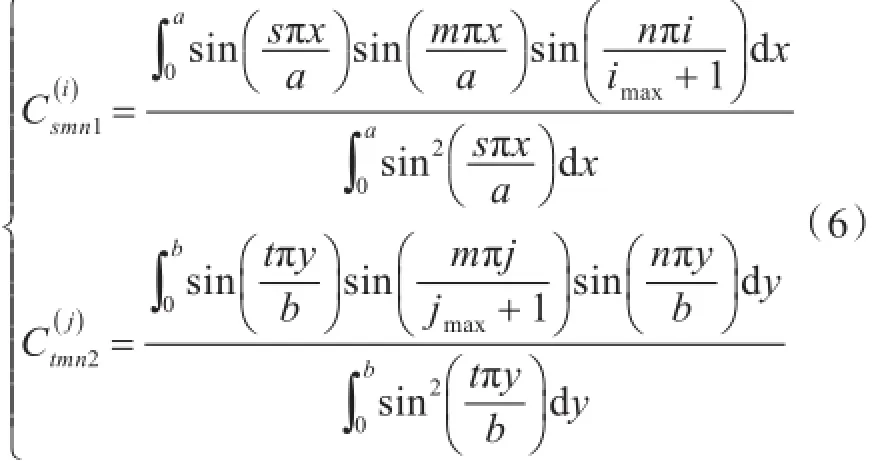
对于纵横离散加筋板的弯曲振动能量方程，引入的质量点与板间满足位移连续条件，因自由振动质量点相对位移很小，故势能可忽略。加筋板在自由振动时，板的能量泛函满足：

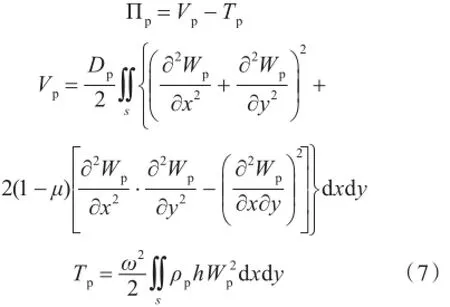
其中：Vp和Tp分别为结构的势能和动能；；h为板厚；ω为圆频率。

梁的能量泛函满足：

将位移函数式（3）代入上式，利用三角函数的积分正交性，可得

引入拉格朗日乘子λ，将加筋板组合结构自由振动分析问题处理成能量泛函变分问题。加筋板的总能量泛函可以表示为

式中：λb1与λb2分别为横向加强筋和纵向加强筋与矩形板组合的拉格朗日乘子，其可由相应加强筋的振型表示：

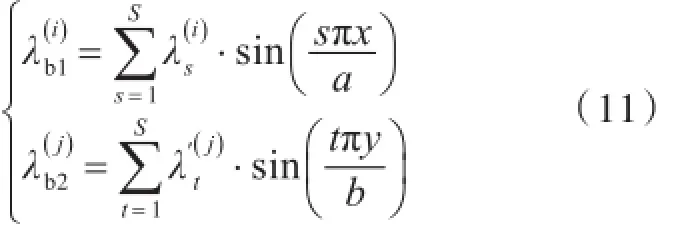
将式（4）和式（5）以及式（11）代入式（10），根据简支梁振型的正交性，将上式化简后可得

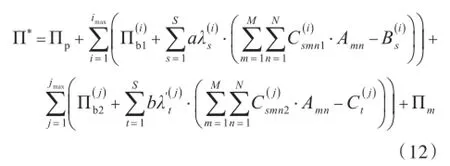
根据最小势能原理，加筋板架结构能量泛函的极值条件为：

将式（7）、式（8）和式（12）代入上式求解可以得到方程组，写成矩阵的形式为

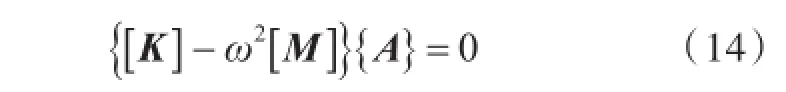
因为幅值Amn不全为零，所以满足

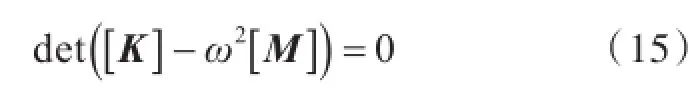
2　实际算例

根据本文方法编制程序，对四边简支附加集中质量点的纵、横加筋矩形板的固有频率进行计算，梁在板上的加筋方式如图2所示。

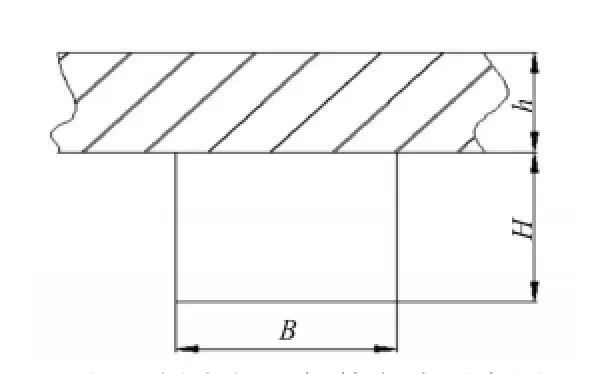
图2　梁在板上加筋方式示意图Fig.2　The layoutofbeam on the plate

假设板和加强筋的材料力学性能相同，数值分析的参数值如表1所示。

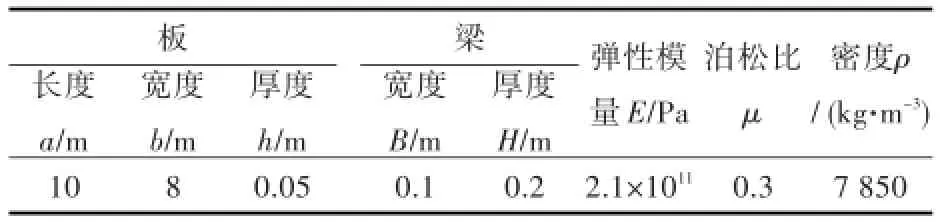
表1　加筋板参数取值表Tab.1　The parametersof the stiffened plate

质量点参数取值如表2所示。

在数值分析过程中选取截断项数M，N，S时，要对函数的收敛性进行分析，故而在解析法计算中选取不同的M，N，S对加筋板振动频率（单位：Hz）进行对比分析，结果如表3所示。

表2　质量点参数取值表Tab.2　The parametersof the equipment

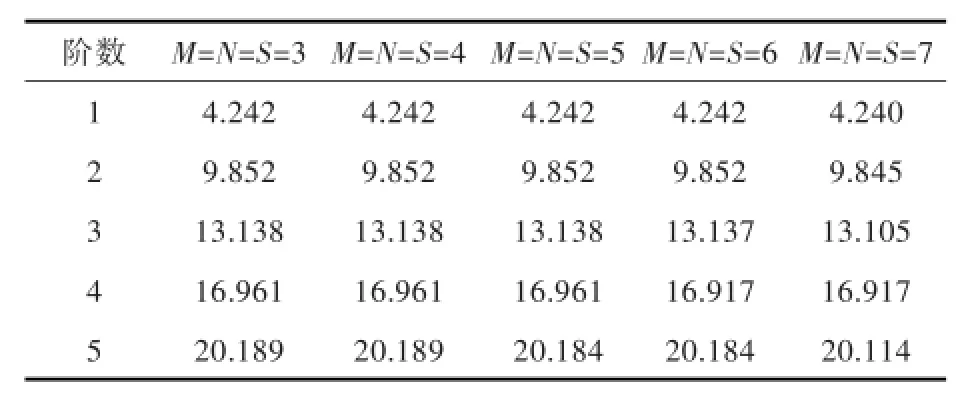
表3　不同M，N，S时加筋板振动频率对比表Tab.3　The vibration frequency of the stiffened p latew ith different M，N，S

根据表3中的数据对比可知，当M=N=S=6时，函数就有较为良好的收敛性。故在运用解析法进行计算时，可以选取截断项数M=N=S=6。

建立算例有限元模型进行仿真分析以验证结果的准确性。附加多个集中质量的加筋矩形板的有限元模型如图3所示。

图3　加筋矩形板的有限元模型Fig.3　The finite elementmodel of the plate

根据振型的关系，可以得出解析方法和有限元模型计算的固有频率的对应关系，加筋板的固有频率（单位：Hz）对比结果如表4所示。表中，振型（i，j）表示加筋板x方向i个半波，y方向j个半波，表征其振型。

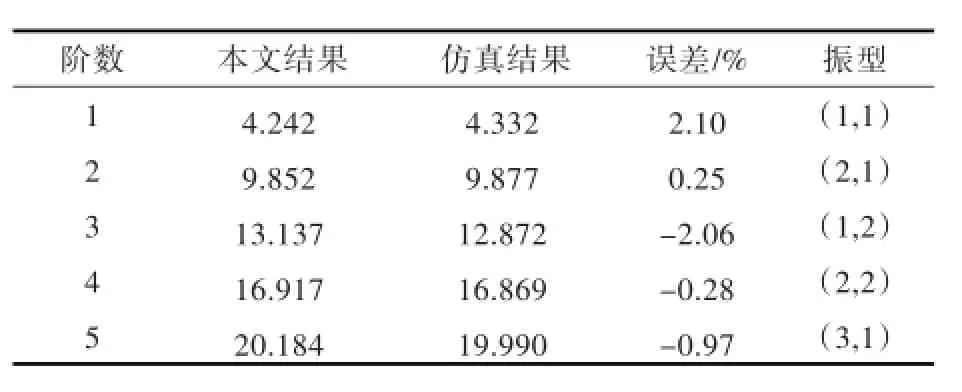
表4　能量法和仿真分析加筋板固有频率对比表Tab.4　The com parison of natural frequency between the energy m ethod and the sim u lation analysis

由表4的数据可知，运用该方法处理附加集中质量的加筋板组合结构问题与有限元仿真分析结果之间的误差很小，该方法的收敛性能好，具有较高的有效性和精度。

3　结论

本文所提出的方法也可用于求解其它边界条件的附加多个集中质量加筋板的固有频率和振型。根据本文方法的理论推导和算例结果对比分析，可以得出以下结论：

1）通过引入拉格朗日乘子，将加筋板组合结构的自由振动问题处理成能量泛函变分问题，对于求解附加多个集中质量加筋板架组合结构的振动问题，具有很好的适用性。

2）本文方法的收敛性较好，因为假定位移函数均为板、梁的真实位移函数，则应用较少的模态便可得出精确度较高的加筋板组合结构的固有频率和振型。

3）以集中质量点的形式引入板上装载设备，可处理任意位置加载设备加筋板的固有频率问题，在方案设计阶段对于解决相关工程问题具有较好的实用性，并且能量法与FEM法结果的对比分析说明了本文方法对于解决附加多个集中质量加筋板自由振动问题的有效性和精确性。

［1］ CHEN C J，LIUW，CHEN SM.Vibration analysis of stiffened plates［J］.Com puters&Structures，1994，50（4）：471-480.

［2］DOWELL E H.Free vibrations of a linear structure with arbitrary support conditions［J］.Journal of Applied Mechanics，1971，38（3）：595-600.

［3］ AZIMI S，HAMILTON J F，SOEDEL W.The receptance method app lied to the free vibration of continuous rectangular plates［J］.Journal of Sound and Vibration，1984，93（1）：9-29.

［4］AKSU G.Free vibration analysis of stiffened plates by including the effect of inp lane inertia［J］.Journal of Applied Mechanics，1982，49（1）：206-212.

［5］ MEAD D J，ZHU D C，BARDELL N S.Free vibration of an orthogonally stiffened flat plate［J］.Journal of Sound and Vibration，1988，127（1）：19-48.

［6］ BISHOP R E D，JOHNSON D C.Themechanics of vibration［M］.Cambridge：cambridge university press，2011.

［7］ GODFRACHT E，ROSENHOUSE G.Use of lagrange multip lierswith polynomial series for dynam ic analysis of constrained p lates part I：Polynom ial series［J］.Journalof Sound and Vibration，1984，92（1）：83-93.

［8］ 曾子平，黄田，HAMILTON JF.任意加筋矩形板的振动分析［J］.振动与冲击，1988（4）：47-53.

ZENG Ziping，HUANG Tian，HAMILTON JF.Vibration analysisof rectangular p latewith any reinforcement［J］.Journal of Sound and Vibration，1988（4）：47-53.

［9］MUKHERJEE A，MUKHOPADHYAY M.Finite element free vibration of eccentrically stiffened plates［J］. Computers&Structures，1988，30（6）：1303-1317.

［10］QING G H，QIU JJ，LIU Y H.Free vibration analysis of stiffened laminated plates［J］.International Journal of Solids and Structures，2006，43（6）：1357-1371.

［责任编辑：田甜］

Free vibration analysisof rectangu lar stiffened p latesw ith several lum ped mass

LIKai1，HE Shutao1，QIU Yongkang2，WUGuomin1，GUOWenjie2，LITianyun2
1 China Ship Developmentand Design Center，Wuhan 430064，China 2 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

Based on themethod of variational energy function，the free vibration characteristics of discrete stiffened plates are studied in this paper.When assessing the deformation coordination constraints of boards and ribs，the vibration analysis problem of stiffened plates is transformed into a classical unconstrained variational problem by introducing Lagrangemultipliers.Through thismethod，a generalized characteristic value ofmatrix equations of stiffened p lates are obtained，and solving the equation set yields the natural frequency of different order for the composite structure.By taking a discrete stiffened p late with four simple edge supported boundary conditions as an examp le，the characteristic values to determine its mode shape are obtained，and the simulation results are compared with those acquired from themulti-stiffened stiffness averagemethod in order to validate the proposed method.Finally，this paper provides a new idea for solving this kind ofengineering problems.

stiffened p late；lum ped mass；Lagrangemu ltip lier；functional variational

U661.44

ADO I：10.3969/j.issn.1673-3185.2015.05.011

2015-02-06网络出版时间：2015-10-8 11∶10

国家部委基金资助项目

李凯（通信作者），男，1983年生，博士，工程师。研究方向：舰船结构振动。E-mail：kaili109@sina.com

网络出版地址：http∶//www.cnki.net/kcms/detail/42.1755.TJ.20151008.1110.026.htm l