水平旋转梁的自由振动分析

南昌航空大学飞行器工程学院 丁相玉

水平旋转梁的自由振动分析

南昌航空大学飞行器工程学院 丁相玉

本文引入一种较新的数学方法阿德米安修正分解法（Adomian modified decomposition method，AMDM）研究在不同边界条件下水平旋转欧拉梁的振动分析。通过与前人的计算结果比较，验证了本文方法的有效性。阿德米安修正分解法提供了一种在任意边界条件下，对旋转梁进行自由振动分析的简单而准确的方法。

Adomian修正分解法；水平旋转梁；边界条件；振形；固有频率；

1 引言

由于旋转梁被广泛应用于旋转机械系统，所以其自由振动分析日益受到重视，并对其进行了广泛的研究，取得了卓有成效的成果。不同的数值分析方法如动态刚度法、经典微分方程法、有限元法和谱元分析法已被用于解决该类结构的自由振动问题。如今，大多数旋转梁的振动分析已不限于经典边界条件（如固定，自由或简支）。然而在实践中，旋转梁的结构特点可能跟经典的边界条件相差甚远。

本文引入一种较新的数学方法——Adomian修正分解法，并将其应用于在各种经典和非经典边界条件下对旋转欧拉梁的自由振动分析。与经典的数值方法如有限元方法相比，Adomian修正分解法的主要优点在于不需要进行离散化从而不用修正误差，并且计算快速。最初提出用来解决物理的前沿问题的Adomian修正分解法，现在已经逐渐被应用于求解振动力学问题。

2 用AMDM方法分析水平旋转梁

如图1所示，欧拉梁绕Z轴旋转，长度为L，梁两端添加弹性约束，在X和Y方向的位移分别为。欧拉梁的自由振动偏微分方程如下所示：

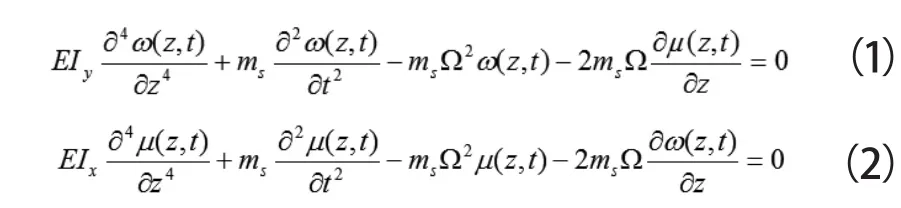
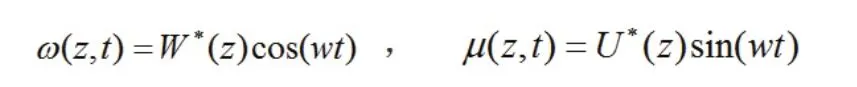
图1 欧拉梁弹性约束

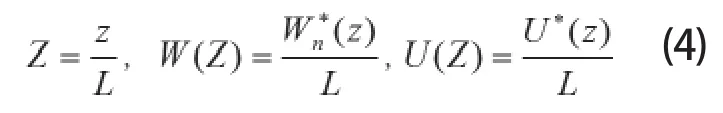
式（1）和（2）重新表示为：

显然式（5）和（6）构成了一个常微分耦合方程。该方程可以简化为矩阵形式

根据Adomian修正分解法可知，式（7）中的可以分解为无穷级数之和

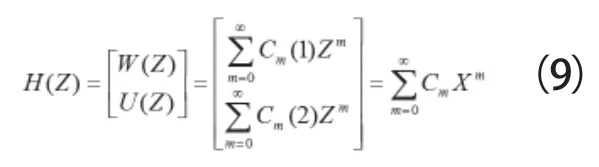
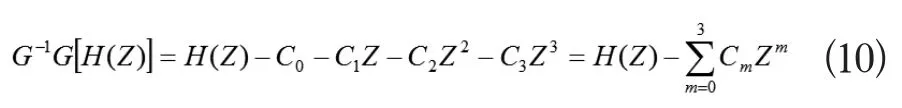
把式（9）代入式（12）的等号右边，并与式（13）进行比较，则公式（9）中的未知向量 可以用以下递推关系确定

根据方程（9）,振型的第一、第二和第三阶空间导数可以表示为

3 梁的固有频率和振型分析

在图1所示的旋转梁无量纲后的两端边界条件可以表示为

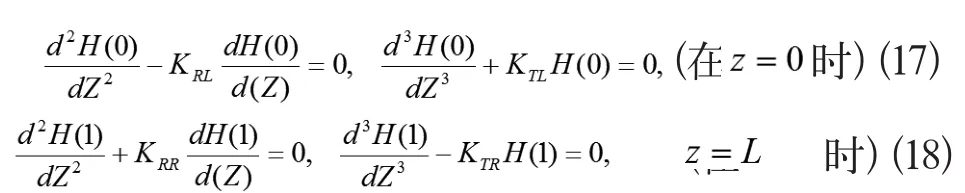
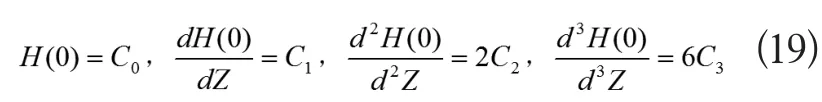
把式（19），（20）代入式（17），（18），可以得到

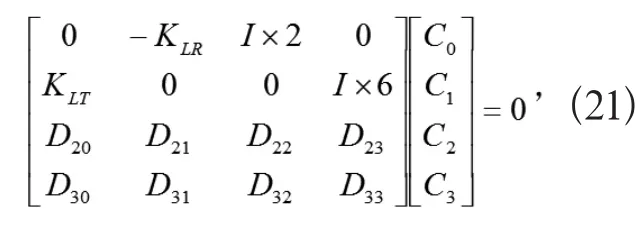
4 数值结果

表1列出了不同旋转速度下的两端简支梁的前六阶无量纲固有频率。将这些计算结果与文献[1]和 [8]进行对比，可以发现利用AMDM方法得到的结果与其他计算方法的结果之间的几乎没有差异。

本文所提出的方法，基于AMDM技术，在任意边界条件下为旋转梁的振动分析提供了一个统一系统的步骤。从而可以很容易的得到无量纲固有频率和相应的振型。例如，通过改变水平和垂直弹簧的刚度数值就可以改变模型的边界条件，但是算法没有任何的影响和改变。

表1 悬臂梁在不同旋转速度下的前六阶无量纲固有频率（当时）

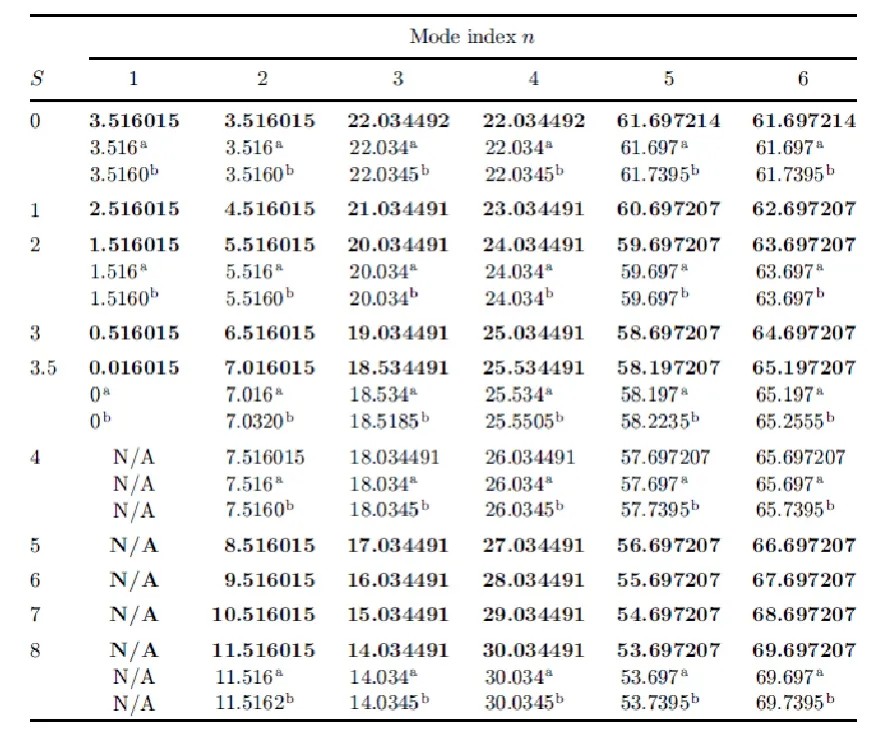
表1 悬臂梁在不同旋转速度下的前六阶无量纲固有频率（当时）

表2 悬臂梁在不同旋转速度下的前六阶无量纲固有频率（当时

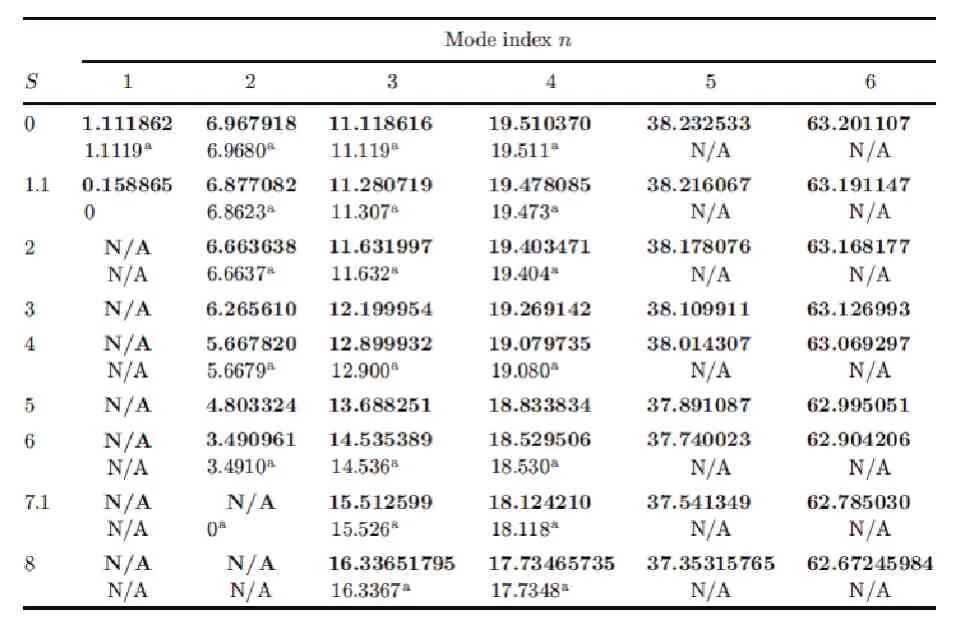
表2 悬臂梁在不同旋转速度下的前六阶无量纲固有频率（当时

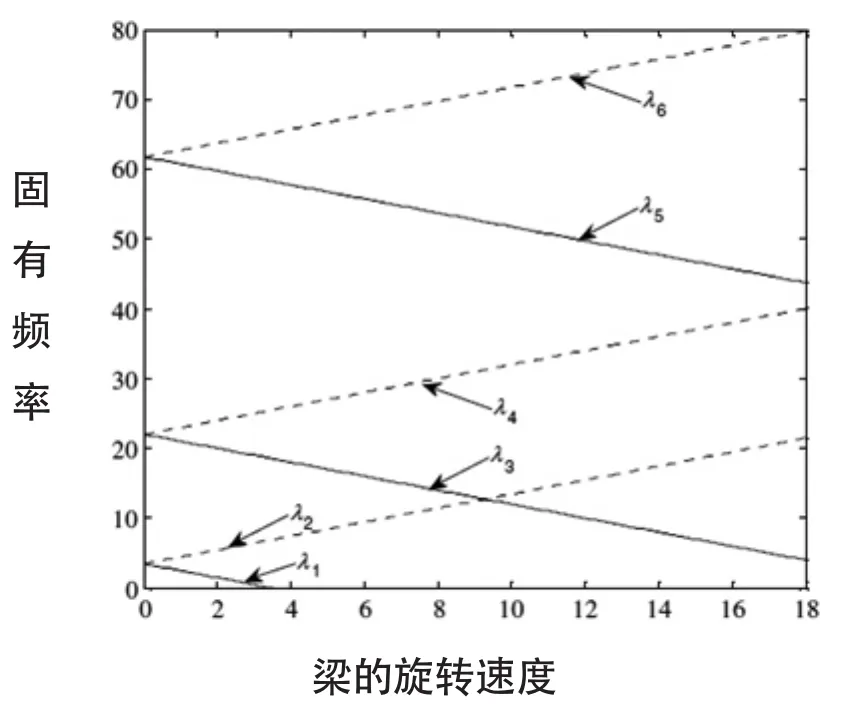
图2 当时悬臂梁的前六阶固有频率

图3 当时悬臂梁的前六阶固有频率

图4 当时固支梁的前六阶固有频率

图5 当时固支梁的前六阶固有频率

5 结论

在本文中，使用AMDM修正方法在不同边界条件下对匀质的旋转欧拉梁的自由振动进行了分析。AMDM修正方法的优点是它的快速收敛性和高精度。用AMDM修正方法针对不同的边界条件和/或旋转速度只需简单地改变相应参数即可，而并不涉及任何程序或算法的修改。通过该方法可以快速的得到各种梁在不同边界条件和旋转速度下的无量纲固有频率。

[1] J.R.Banerjee and H.Su,Development of a dynamic stiffness matrix for free vibration analysis of spinning beams,Comput.Struct.82(2004)2189–2197.

[2] J.R.Banerjee and H.Su,Dynamic stiffness formulation and free vibration analysis of a spinning composite beam,Comput. Struct.84(2006)1208–1214.

[3] S.Na,H.Yoon and L.Librescu,Effect of taper ratio on vibration and stability of a composite thin-walled spinning shaft,Thin-Walled Structures 44(2006) 362–371.

[4] W. R.Chen,On the vibration and stability of spinning axially loaded pre-twisted Timoshenko beams,Finite Elem.Anal.Des.46(2010)1037–1047.

[5] K.B.Mustapha and Z.W.Zhong,Spectral element analysis of a non-classical model of a spinning micro beam embedded in an elastic medium,Mech.Mach.Theory 53(2012)66–85.

[6] G.Adomian,Solving Frontier Problems of Physics:The Decomposition Method(Kluwer-Academic Publishers,Boston,1994).

[7] J.C.Hsu,H.Y.Lai and C.K.Chen,Free vibration of non-uniform Euler–Bernoulli beams with general elastically end constraints using Adomian modified decomposition method,J.Sound Vib.318(2008)965–981.

[8] Q.Mao and S.Pietrzko,Free vibration analysis of a type of tapered beams by using Adomian decomposition method,Appl.Math.Comput.219(2012)3264–3271.

[9] 朱由锋,任勇生.基于有限差分法的水平旋转梁自由振动解析[J].振动与冲击,2012,31(14):43-46.

丁相玉(1983-)，男，硕士。研究方向为航空发动机振动分析。