射流循环DTB结晶器内的CFD模拟
李继翔,郝婷婷,兰忠,马学虎
(大连理工大学化学工程研究所,辽宁省化工资源清洁利用重点实验室,辽宁 大连 116024)
引 言
自Randolph 等[1]将粒数衡算引入工业结晶过程,将产品粒度分布(CSD)与结晶器结构以及操作参数联系起来,结晶理论获得了飞速发展。
DTB 结晶器是20 世纪50年代出现的一种具有细晶消除系统的复杂结构结晶器,经多年运行考察,证明可以生产较大的晶粒,其流体力学条件好,对传质速率控制的结晶过程有较高的生长速率[2]。早期的R-Z 模型[1]假设结晶器内物性均匀,但由于真实的DTB 结晶器内物性并不均匀,Kramer 等[3]提出了组块模型,将DTB 结晶器分为不同的区域,不同区域具有不同的物性与功能,更好地预测了CSD。
随着计算机的发展,CFD 技术以其能更准确再现物理过程的特点,在结晶过程中发挥了巨大作用。Bałdyga 等[4]通过CFD 模拟硫酸钡在管中的沉淀过程,通过矩量法求解粒数衡算方程,并与动量微分方程等耦合,得到了沉淀结晶的CSD。Wei 等[5]也利用商业软件Fluent 将矩量法求解的粒数衡算方程引入流体力学过程的计算中,通过求解标量输运方程,获得流体力学性质与粒数分布的关系,发现搅拌速率对平均粒径有显著影响。
但矩量法忽略了固体颗粒与流体间的相互作用,不能很好地描述大颗粒结晶体系的水力学性质。因此很多学者也针对DTB 结晶器做了很多流体力学方面的研究,Wantha 等[6]针对DTB 结晶器进行了多相流的数值模拟,以动量源相简化搅拌桨模型,获得了结晶器内的循环流场。武首香等[7]利用欧拉多相流模型,考察了DTB 结晶器内的流场、过饱和度分布及晶体颗粒的浓度分布。通过分组法,关联了粒数衡算与流体力学方程,获得了产品粒度分布。Song 等[8]考察了螺旋桨、PBT 搅拌桨和Rushton搅拌桨3 种桨形对DTB 结晶过程颗粒悬浮的影响,模拟过程中忽略了晶体的成核、生长。结果表明,螺旋桨能在最低能耗下实现结晶器内的颗粒悬浮。Rane 等[9]总结了11 种工业结晶器的CFD 模拟条件及结果,认为强制循环蒸发结晶器和真空间歇结晶器无法获得大颗粒产品,而DTB 结晶器可以获得大至5 mm 的颗粒。
由于DTB 结晶器属于搅拌式反应结晶器,其外形结构、搅拌桨类型以及操作方式对结晶过程的流体力学状态都会产生重要影响[10-11]。周学晋等[12]认为由外循环实现DTB 结晶器结晶过程,可以避免由搅拌桨与晶体碰撞引发的二次成核,对产品粒度的提高有一定优势,并避免了搅拌轴的密封问题,降低了设备成本,但并未对结晶器结构及操作参数对水力学的影响做出细致分析。
射流混合广泛应用在固液混合中[13],很多学者对射流的特性也做了大量的研究[14-18]。用射流喷嘴实现DTB 结晶器内搅拌桨的功能,提高外循环母液带动结晶器晶浆内循环的效率,是很好的思路。刘晓燕[19]利用此技术设计中试DTB 结晶器,但产品粒度偏低,平均粒度为0.4 mm,分析认为因为水力学性质欠佳,晶浆密度及过饱和度分布不均匀,入口进料未能充分带动结晶器内晶浆内循环,因此针对射流混合实现DTB 结晶器内晶浆的均匀混合进行研究,对提高射流混合DTB 结晶器产品粒度有着重要意义。
本文设计实验级DTB 结晶器模型,利用数值方法,对DTB 结晶器中射流流形进行了分析,考察了不同入口直径,不同入口流速,不同导流筒结构,对DTB 结晶器的轴线速度,轴向速度分布,特征半宽度及循环速率比的影响,并利用多相流模型验证,进行结晶器优化。
1 数值模拟方法
1.1 物理模型
本文设计实验级射流混合DTB 结晶器,有效体积为13 L,具体结构如图1 所示,网格划分如图2 所示。射流自底部入口喷嘴射出,由于射流的卷吸作用,带动周围静止流体流动,稳态时,将有流量为Q 的流体进入导流筒,并从导流筒挡板间的环形通道返回,其中流量Q0的物流进入结晶器壳体与挡板间的环隙,并从两侧的出口排出,其余流体进入导流筒进行内循环,实现过饱和度与颗粒浓度的均匀分布,为制备大颗粒硫酸铵提供先决条件。
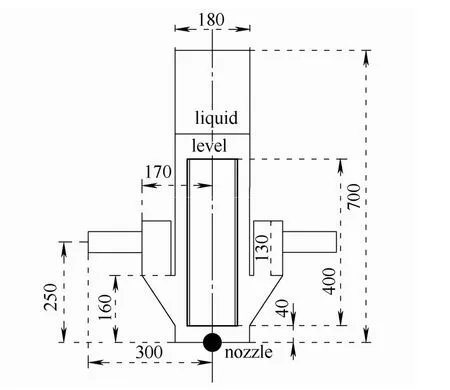
图1 实验室级DTB 结晶器结构Fig.1 Structure diagram of laboratorial DTB crystallizer

图2 实验级DTB 结晶器的网格划分Fig.2 Grid of laboratorial DTB crystallizer
1.2 模拟方法
本文利用Fluent 软件,采用QUICK 离散格式,压力场由SIMPLE 算法求解,应用RNG k-ε 湍流模型。利用Gambit 前处理软件,将整个计算域分为7个区域,除锥形区外均用结构化网格划分,底部射流入口边界条件为速度入口,湍流条件由湍动强度及水力学直径设置,湍动强度由式(1)估计;顶部假定为静液面,选取对称边界条件;两侧出口为压力出口,压力为由Aspen 软件计算的60℃下硫酸铵饱和溶液的蒸气压,20 kPa,回流的湍流条件根据湍动强度及水力学直径设置。各区域间的界面设置为内界面,标记导流筒入口及出口,方便之后的数据处理;结晶器壳体等结构取壁面边界条件。经网格无关性实验,以网格数为15 万个为宜。多相流模型采用欧拉多相流模型,选取Syamlal-O’Brien 曳力模型,碰撞系数取0.9,考察颗粒的浓度分布情况,颗粒粒径取1 mm。首先用稳态单相流模型获得最佳的结晶器结构,之后用非稳态多相流模型验证,以进入导流筒的颗粒相质量流量为恒定值时为稳定条件,考察其颗粒浓度分布,多相流时间步长取0.05 s。

1.3 模型验证

图3 特征半厚度模拟值与实验值的对比Fig.3 Comparison of experimental and simulated values of be
关于射流混合DTB 结晶器内流体力学性质的 实验鲜有报道,难于直接进行模型验证,但对于圆形湍动射流的模拟实验有较多研究。Parham 等[20]利用RNG k-ε 模型模拟了三角形喷嘴下的对置式冲击射流,考察了平均速度、压力分布及湍动特性等,模拟结果与文献实验结果符合很好,验证了模型计算的准确性。Guo 等[21]利用RNG k-ε 模型,模拟了横流中的单股射流,计算与实验的结果吻合较好。速度特征值半厚度be是描述射流沿流程发展的重要参数。以数值模拟结果中导流筒内主体段的特征半宽度为例,对比华明等[15]和董志勇[17]的实验数据,可见射流发展的趋势很接近,模型计算有较好的准确性。
2 模拟结果与讨论
由于循环物流全部经导流筒向上流动,考察导流筒内的流场可以获得结晶器内流体的循环情况。结晶器内的流动状态为有较为复杂边界约束的圆形湍动冲击射流,导流筒内的射流可近似考虑为湍动冲击射流的自由射流区,但由于有侧壁面,应考虑导流筒壁面对射流的约束作用,以及其循环流体的作用。本文利用数值模拟,考察导流筒内半径RT为45、50、55、60 mm,即导流筒挡板间环隙面积与导流筒横截面积比β 为2.7、2.0、1.5、1,入口直径d0为8、12、16、23 mm,入口流速为u0为2、4、6、8 m·s-1等64 种情况时,DTB 结晶器内的流体力学性质。
2.1 轴线速度
本文利用Fluent 的输出功能,取不同单相流稳态模拟实例中轴线上各个节点的轴线速度。从图4可见,对于本文结构的结晶器,当RT为50 mm,入口直径为12 mm 时,不同入口流速下,轴线速度衰减趋势相同,当x/H<0.6 时,u0/um,即入口流速与轴线速度的比值,随 x/d0线性增加;当0.6

根据后文循环速率的模拟结果,对于一定结构的结晶器,其循环流量与入口流速呈正比,因此认为环境流速ua正比于u0,对x/H<0.6 时的线性段进行拟合得到式(3)。当0.6

即

从图5 可见,当RT发生变化,β 减小时,轴线速度变化偏离同向圆形自由湍动射流并有减小的趋势。分析原因,由于环隙面积的减小,加大了循环流体的阻力,从导流筒顶部排出的流体,不能很好地经环隙循环至底部,重新进入射流。从趋势上看,随着β 增大,导流筒内的轴线速度变化逐浙趋近于式(3)。当β 较低时,利用式(3)预测的轴线速度,会过高地估计结晶器轴线流速,因此引入效率系数η。且由图4 分析,不同流量下轴线速度几乎不变, 可见影响效率系数的为比值而非绝对值,因此假定η 仅是β 及H/d0的函数,如式(4)
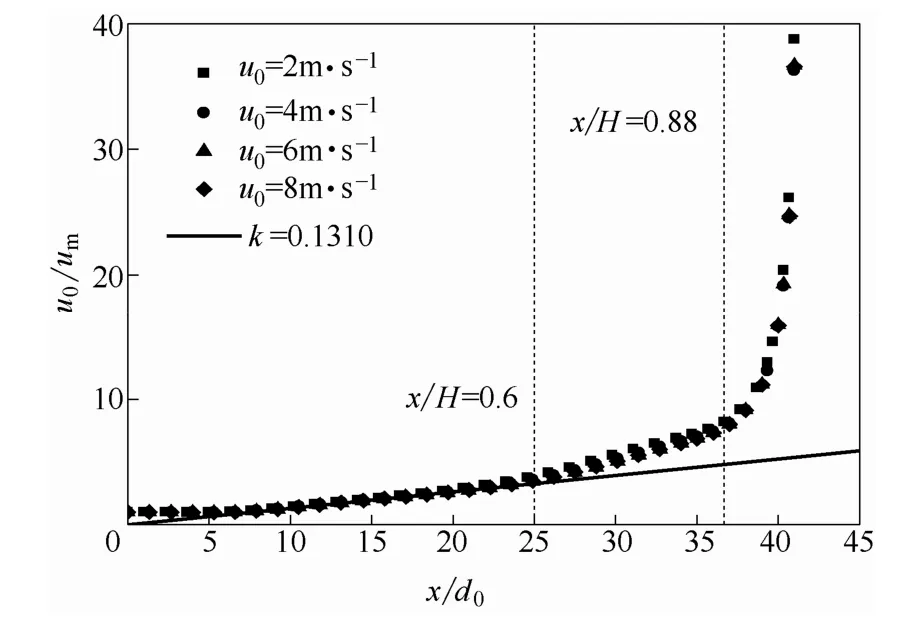
图4 不同入口流速下的轴线速度变化Fig.4 Trend of u0/um with x/d0 in different inlet velocity

图5 不同导流筒直径下轴线速度变化Fig.5 Trend of u0/um with x/d0 in different diameter of tube

2.2 速度特征半厚度
射流特征半厚度be,它的位置定义为当r=be时,该位置轴向速度与同高度下轴线速度的比值u/um=1/e。实验证明[17]射流线性扩展,be正比于流程,对于圆形自由湍动射流be=cx,c=0.114。余常昭[18]和华明等[15]的实验也验证了圆形自由湍动射流主体段的线性扩展。
本文对d0=16 mm,u0=4 m·s-1时,RT为45、50、55 mm 的特征半厚度进行考察。利用Fluent 的等值面输出功能,在过轴线且垂直于出口轴线的截面上,输出导流筒内轴向速度为特征速度时的坐标位置,取距轴心的平均值。
从图6 中可以看出,当入口直径及入口流速一定时,导流筒直径对导流筒内射流主体段的速度特征半厚度影响不大,当特征半厚度小于导流筒半径时,射流随流程线性扩展,扩散系数c=0.1126。当到达半径以后,由于特征速度出现在边界层中,不能准确描述速度分布特征,因此到达半径后的特征半厚度取前段线性趋势外延。
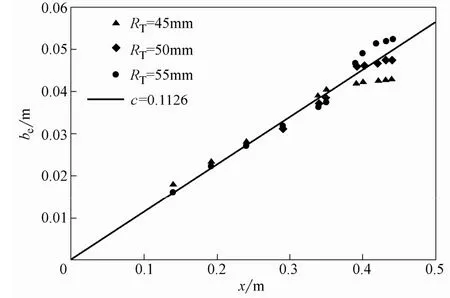
图6 不同导流筒直径下的特征半厚度Fig.6 Trend of development of jet along flow distance
2.3 轴向速度分布
以RT=50 mm,d0=23 mm,u0=2、6 m·s-1两种情况为例,选取导流筒内过结晶器轴线且垂直于出口轴线的截面进行量纲1 轴向速度u/um的分析。轴线速度与速度半宽值为2.1、2.2 节所述。
从图5、图6 可以看出,当入口直径为23 mm时,在特征半厚度内的量纲1 轴向速度分布与高斯分布符合得很好,特征半厚度外的流体量纲1 轴向速度分布趋势偏离高斯分布,而且变化趋势并不随入口流速而变化。当x=140、240 mm 时,即x/H<0.6时,be外的速度分布要高于高斯分布的估计,考虑是由于循环流未充分融入射流主体的原因。当循环流由于卷吸作用,充分进入射流主体时,导流筒内的速度分布几乎完全满足高斯分布,因此可以由导流筒出口处的量纲1 轴向速度分布获得流经导流筒的内循环流量。
2.4 循环速率
由于射流的卷吸作用,射流流量随流程增加而增加,并在到达结晶器静液面后从导流筒挡板间环隙返回,形成循环流,流量为Q0的流体从出口排出,其余流体进入导流筒,由导流筒入口做物料衡算,越高的循环速率比,整个系统浓度越均一,结晶器系统越稳定,有利于大颗粒晶体的生长。很多学者对圆形自由湍动射流的流量沿流程的变化做了分析[17],余常昭等[23]也考察了圆形断面自由湍动射流的卷吸特性,同时也分析了射流卷吸作用的原因,但对于射流混合DTB 结晶器内的流动状态研究较少。设循环速率比γ 为内循环流量Qr与进料量 Q0之比为,即由于射流卷吸作用带动的额外循环流量与自身流量的比值。
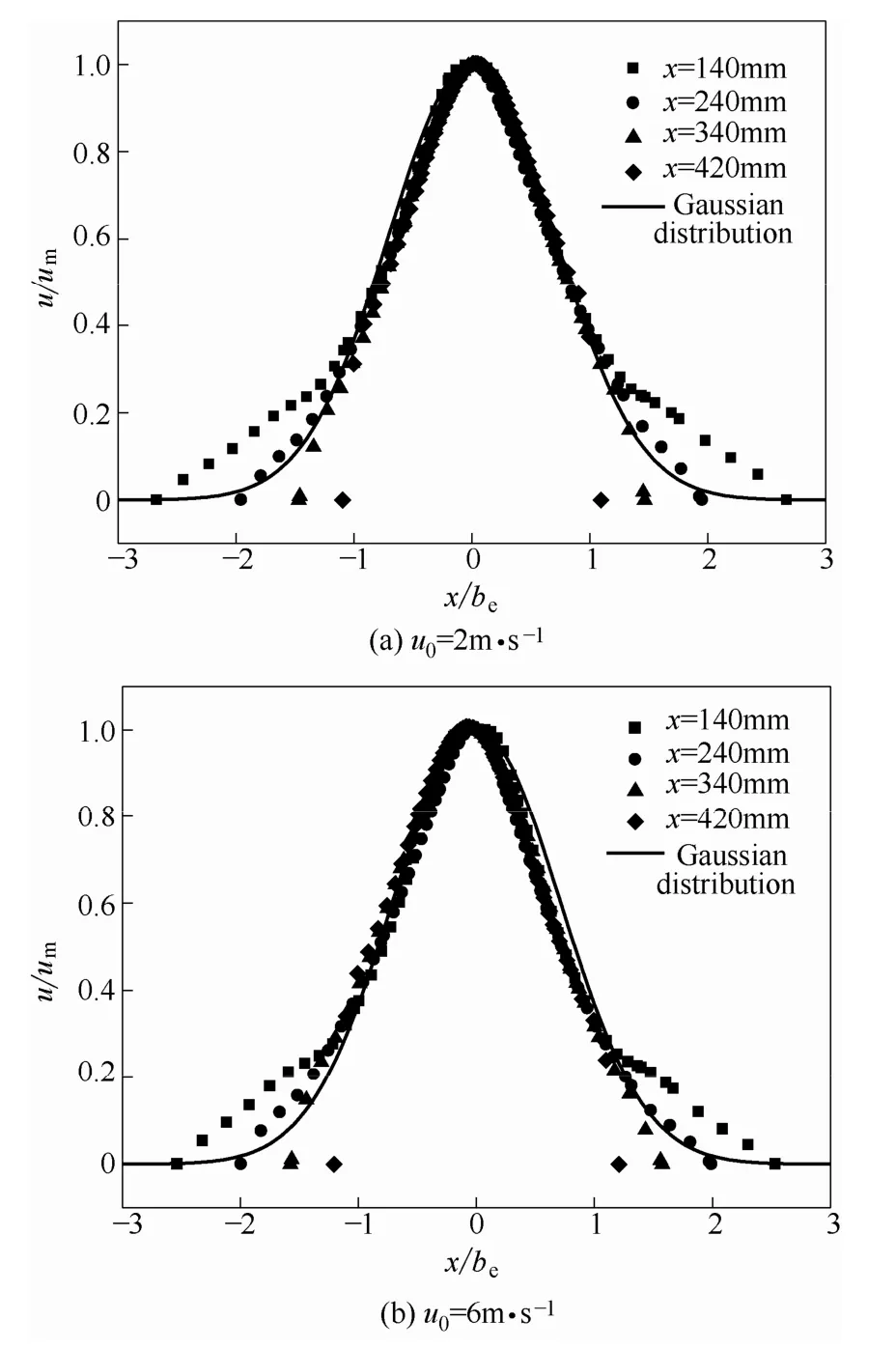
图7 不同入口速度下的轴向速度分布Fig.7 Dimensionless axial velocity distribution in different inlet velocities
2.4.1 循环速率比 利用数值模拟,考察导流筒半径RT为45、50、55、60 mm,即导流筒挡板间环隙面积与导流筒横截面积比β 为2.7、2.0、1.5、1,入口直径d0为8、12、16、23 mm,入口流速为u0为2、4、6、8 m·s-1等64 种情况的循环速率比,分析循环速率比随H/d0的变化趋势。
从图8 中可知,在相同导流筒结构下,不同流速,循环速率比γ 随H/d0的变化趋势几乎相同,呈很好的线性。
对比图9 中不同导流筒直径下的循环速率比的变化趋势,可见在入口直径8~23 mm 范围内,满足良好的线性趋势,所有拟合的直线R2在0.995 以上。循环速率比γ 随H/d0变化的趋势与β 有关,呈现先增大再减小的趋势,当β=2.0 时斜率最高,此时的结晶器内部结构最佳。
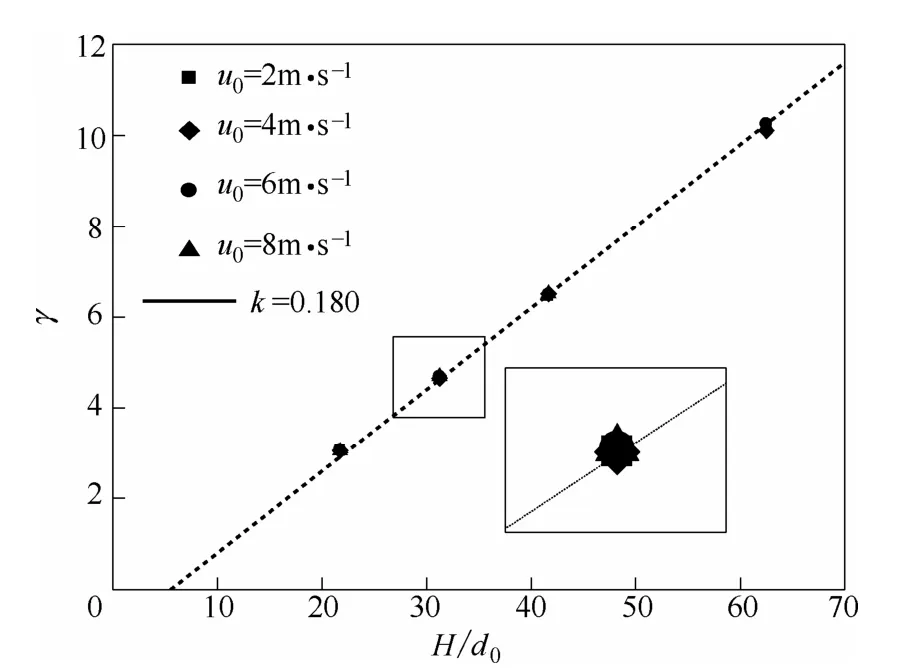
图8 不同入口流速循环速率比随入口 直径的变化(β=2.0)Fig.8 Trend of circulation flow ratio with H/d0 in different inlet velocities (β=2.0)
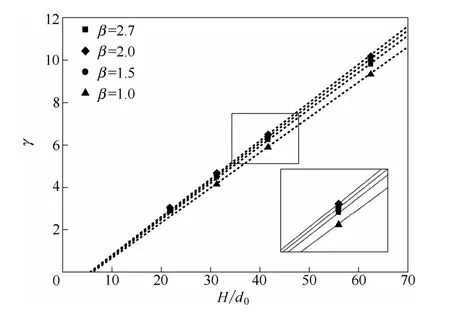
图9 不同导流筒直径下的循环速率比Fig.9 Trend of circulation flow ratio with H/d0 in different diameters of tube
2.4.2 循环速率比的预测 根据上文分析,当循环速率稳定时,由于导流筒壁面约束,筒内各截面处轴向流量恒定。且由图7 可见,导流筒出口处量纲1 轴向速度分布满足高斯分布,边缘未出现偏离,因此以导流筒出口处速度分布计算循环流量更为准确,其中导流筒高度HT=αH=440 mm,特征半宽度由发展段趋势外延获得,即beout=0.1126αH。轴线速度由效率系数修正,获得式(5)

轴向速度
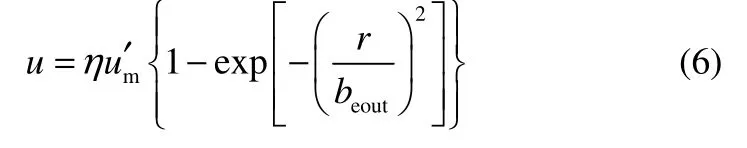
以导流筒出口速度分布,估计全循环流量
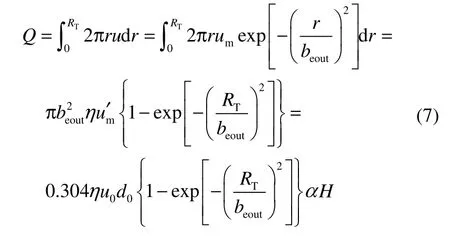
循环速率比

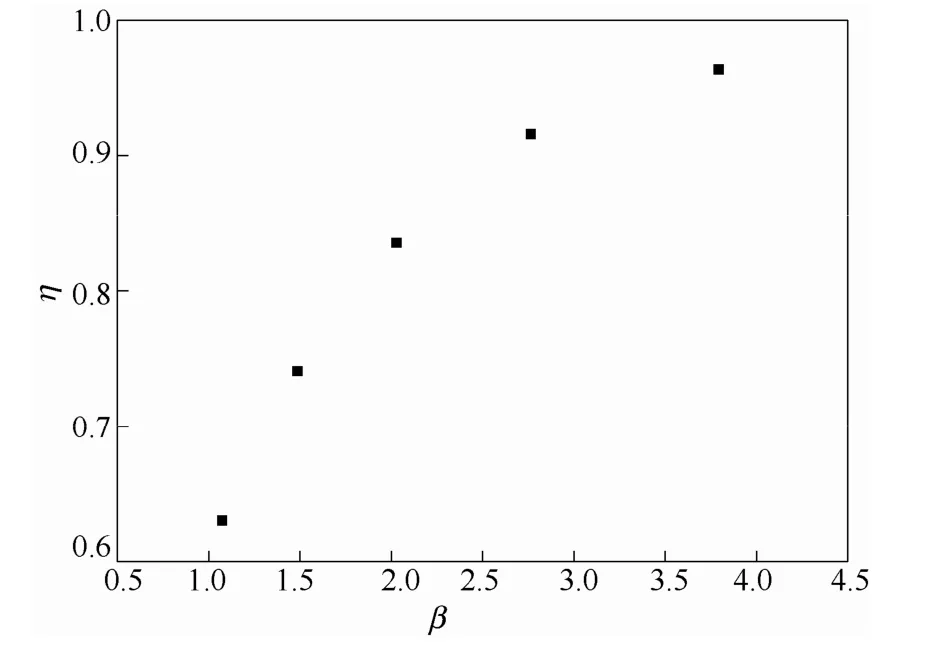
图10 效率系数随面积比的变化Fig.10 Trend of efficiency coefficient with β
从图9 可见,循环速率比对于H/d0呈良好线性,斜率为常数,结合式(8),可知在一定导流筒半径下,效率系数对于d0是常数,因此认为效率系数在入口直径8~23 mm 的范围内,随入口直径变化几乎可忽略不计。而利用式(8)及循环速率数据可获得不同面积比β 下的效率系数η。由图10 可见,随着面积比β 增加η 趋近于1。
2.5 多相流实验
根据上文结果,选取RT=50 mm 的结晶器。由于入口直径过小时,为达到相同入口流量,流速增加,功率平方增长,综合考虑,取d0=12 mm,u0=8 m·s-1进行实验。由于晶体颗粒在结晶器内接近流化床流动状态,因此利用欧拉法模拟多相流,对设计结晶器内进行多相流模拟验证,晶粒颗粒粒度为1 mm,颗粒相的体积分数为0.15。系统平衡时,即通过导流筒的颗粒相质量流量恒定时,结晶器内颗粒浓度分布如图11 所示。分布整体较为均匀,底部及锥形区略有沉积,导流筒中颗粒浓度分布沿径向方向减小。循环速率模拟结果比为6.42,单相流结果为6.5,较单相流结果偏低。分析为由于流体克服与颗粒的曳力引起的流场变化。

图11 射流混合结晶器内的晶浆浓度分布Fig.11 Concentration distribution of particle in DTB crystallizer
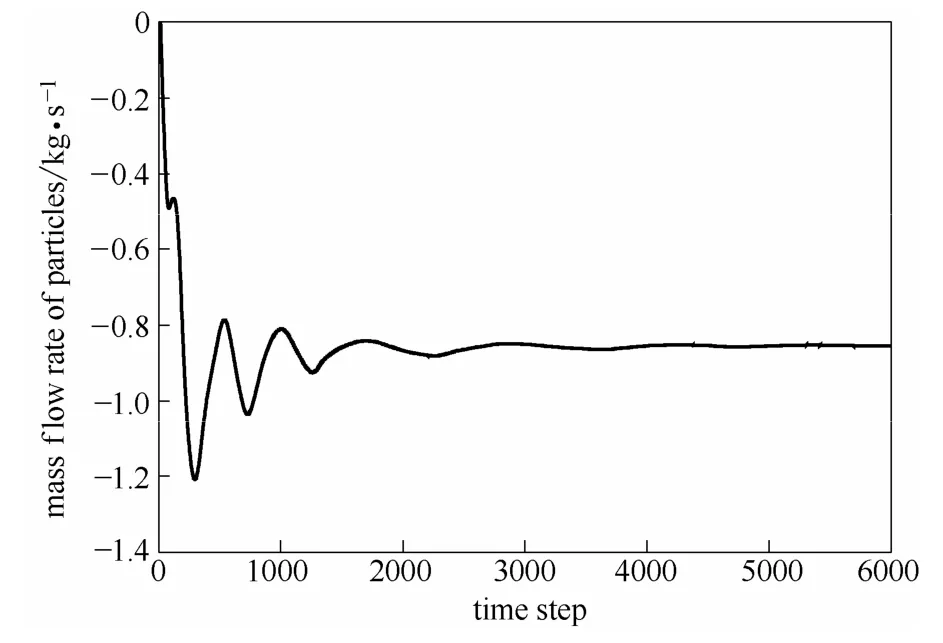
图12 导流筒内颗粒相流量随时间的变化Fig.12 Trend of flow rate cross tube of particle with time
3 结 论
本文以设计的实验级DTB 结晶器为例,利用数值方法,对DTB 结晶器中射流流型进行了分析,选取了最优结构,并利用多相流模型进行验证,结论如下。
(1)由于导流筒壁面及循环流的作用,导流筒内射流轴线速度在刚进入导流筒内的射流段,即x/H<0.6 时,接近同向射流,呈良好线性;当0.6 (2)速度特征半厚度随流程呈良好的线性,量纲1 轴向速度分布基本满足高斯分布。刚进入导流筒时,由于循环流未融入射流主体而引起边缘流速高于高斯分布,充分发展后,导流筒内射流的量纲1 轴向速度分布可由高斯分布描述。 (3)循环速率比γ 与H/d0及β 有关。H/d0一定时,随β 先增大再减小,存在最优值,本例中以β=2.0为佳;β 一定时,γ 随H/d0线性增大。 (4)利用射流混合可以较好地实现DTB 结晶器内颗粒浓度的均匀分布,但导流筒中颗粒浓度分布沿径向方向减小,且其循环速率比较单相流时较低。 符 号 说 明 be——速度特征半厚度,m beout——导流筒出口处特征半厚度,m c ——射流扩散系数 d0——射流入口直径,mm H ——结晶器静液面高度,mm HT——导流筒出口高度,mm Q ——流经导流筒的流体体积流量,m3·s-1 Qr——流经导流筒的内循环流体体积流量,m3·s-1 Q0——入口体积流量,m3·s-1 RT——导流筒半径,mm u ——轴向速度,m·s-1 um——轴线速度,m·s-1 u0——入口流速,m·s-1 x ——流程,m α ——导流筒出口高度比 β ——导流筒挡板间环隙面积与导流筒横截面积比 γ ——循环速率比 η ——轴线速度效率系数 [1]Randolph A D, Larson M A.Theory of Particulate Processes [M].2nd ed.New York: Academic Press, 1988. [2]Ding Xuhuai(丁绪淮).Industrial Crystallization (工业结晶)[M].Beijing: Chemical Industry Press, 1985:60-67. [3]Kramer H J M, Dijkstra J W, Verheijen P J T, Van Rosmalen G M.Modeling of industrial crystallizers for control and design purposes [J].Powder Technology, 2000, 108(2): 185-191. [4]Bałdyga J, Orciuch W.Barium sulphate precipitation in a pipe—an experimental study and CFD modelling [J].Chemical Engineering Science, 2001, 56(7): 2435-2444. [5]Wei H, Zhou W, Garside J.Computational fluid dynamics modeling of the precipitation process in a semibatch crystallizer [J].Industrial & Engineering Chemistry Research, 2001, 40(23): 5255-5261. [6]Wantha W, Flood A E.Numerical simulation and analysis of flow in a DTB crystallizer [J].Chemical Engineering Communications, 2008, 195(11): 1345-1370. [7]Wu Shouxiang(武首香), Wang Xuekui(王学魁), Sha Zhuoliang(沙作良), Wang Yanfei(王彦飞).Solution of population balance in multiphase flow field for industrial crystallization process [J].CIESC Journal (化工学报), 2009, 60(3): 593-600. [8]Song Xingfu, Zhang Menghua, Wang Jin, Li Ping, Yu Jianguo.Optimization design for DTB industrial crystallizer of potassium chloride [J].Industrial & Engineering Chemistry Research, 2010, 49(21): 10297-10302. [9]Rane Chinmay V, Ganguli Arijit A, Kalekudithi Ekambara, Patil Raosaheb N, Joshi Jyeshtharaj B, Doraiswami Ramkrishna.CFD simulation and comparison of industrial crystallizers [J].The Canadian Journal of Chemical Engineering, 2014, 92(12): 2138- 2156. [10]Sha Z, Oinas P, Louhi-Kultanen M, Yang G, Seppo Palosaari.Application of CFD simulation to suspension crystallization—factors affecting size-dependent classification [J].Powder Technology, 2001, 121(1): 20-25. [11]Sha Z, Laari A, Turunen I.Multi-phase-multi-size-group model for the inclusion of population balances into the CFD simulation of gas-liquid bubbly flows [J].Chemical Engineering & Technology, 2006, 29(5): 550-559. [12]Zhou Xuejin(周学晋), Yuan Jianjun(袁建军), Sha Zuoliang(沙作良), He Hua(贺华).Characteristics of computational fluid dynamics in external-cycling fluidized DTB crystallizer [J].Journal of Salt and Chemical Industry(盐业与化工), 2011, 40(3): 30-33. [13]Shi Jun(时钧).Chemical Engineering Handbook(化学工程手册)[M].2nd ed.Beijing:Chemical Industry Press,1996: 20-21 [14]Chu P C K, Lee J H, Chu V H.Spreading of turbulent round jet in coflow [J].Journal of Hydraulic Engineering, 1999, 125(2): 193-204. [15]Hua Ming(华明), Tang Hongwu(唐洪武), Wang Huimin(王惠民), Wang Zhiliang(王志良).Investigation of turbulent characteristics of velocity field of a round jet using ADV measurement techniques [J].Journal of Nanjing Hydraulic Research Institute(水利水运科学研究), 2000, (3): 18-21. [16]Donaldson C D, Snedeker R S.A study of free jet impingement(Ⅰ): Mean properties of free and impinging jets [J].J.Fluid Mech., 1971, 45(2): 281-319. [17]Dong Zhiyong(董志勇).Jet Mechanics(射流力学)[M].Beijing: China Science Publishing, 2005: 25-26. [18]Yu Changzhao( 余常昭).Turbulent Jets( 紊动射流)[M].Beijing:Higher Education Press,1993 [19]Liu Xiaoyan(刘晓燕).Experimental investigation and design of crystallizer of concentrated seawater[D].Dalian: Dalian University of Technology, 2012. [20]Parham K, Esmaeilzadeh E, Atikol U, Aldabbagh L B Y.A numerical study of turbulent opposed impinging jets issuing from triangular nozzles with different geometries [J].Heat and Mass Transfer, 2011, 47(4): 427-437. [21]Guo Tingting, Li Shaohua, Xu Zhong.A numerical simulation of three-dimensional turbulent jets in crossflow [J].Proceedings of Chinese Society for Electrical Engineering, 2003, 23(7): 191-195. [22]Xiao Yang(肖洋), Tang Hongwu(唐洪武), Hua Ming(华明), Wang Zhiliang( 王 志 良).Experimental investigation on mixing characteristics of a round jet in co-flow [J].Advances in Water Science(水科学进展), 2006, 17(4): 512-517. [23]Yu Changzhao(余常昭), Li Chunhua(李春华).Experimental study on the entrainment for turbulent round jets [J].Aerodynamic Experiment and Measurement & Control(气动实验与测量控制), 1996, 10(1): 31-38.

