考虑不确定复合控制系统动态特性的前向拦截三维导引律
张友安,吴华丽,梁 勇,张金鹏
(1.海军航空工程学院控制工程系,山东烟台264001;2.中国空空导弹研究院,河南洛阳471099;3.航空制导武器航空科技重点实验室,河南洛阳471099)
考虑不确定复合控制系统动态特性的前向拦截三维导引律
张友安1,吴华丽1,梁 勇1,张金鹏2,3
(1.海军航空工程学院控制工程系,山东烟台264001;2.中国空空导弹研究院,河南洛阳471099;3.航空制导武器航空科技重点实验室,河南洛阳471099)
为实现高空高速目标的精确拦截,研究了考虑直接力气动力复合控制动态特性及不确定性的前向拦截三维导引律设计方法。对采用复合控制的慢旋导弹的动力学模型进行了线性化处理,在气动舵控制的基础上设计连续直接力,然后对其进行离散化处理,避免复杂的控制分配问题。在三维弹目相对运动模型和不确定导弹动力学线性化模型的基础上,利用时标分离的思想将系统划分为慢变子系统和快变子系统,应用基于李雅普诺夫稳定性理论的鲁棒控制方法对慢变子系统和快变子系统分别进行鲁棒动态逆设计,得到考虑不确定复合控制系统动态特性的前向拦截三维导引律。对单通道控制和双通道控制的情况分别进行了仿真研究,验证了本文方法的正确性和有效性。
李雅普诺夫稳定性;直接力气动力复合控制;前向拦截;三维导引律;鲁棒动态逆
0 引 言
按照拦截导弹与目标的相对位置与相对速度的关系,传统的拦截方式可分为迎头拦截和尾追拦截。迎头拦截会使弹目之间的相对运动速度非常大,导致末制导的剩余时间更短,对拦截导弹过载能力的要求就更高;尾追拦截要求导弹的速度大于目标速度,对拦截器的能量设备要求过高而难以实现。因此,文献[1-2]提出了前向追击拦截导引方式,建立了二维前向追击拦截导引运动模型。对于大气层内使用连续气动舵控制的拦截器,在不考虑弹体动态特性以及过载限制的理想情况下,设计了前向追击拦截导引律;对于大气层外的拦截弹,基于喷气直接力控制设计了Bang-Bang控制导引律。文献[3]设计了基于变结构控制的前向拦截导引律,分析了导引品质明显优于采用迎头拦截的导引规律,但没有考虑弹体动态特性的影响。文献[4-5]建立了目标和拦截器的三维制导模型,设计了三维非线性变结构前向拦截制导律,但是都将导弹视为质点,忽略了弹体的动态特性。文献[6-7]将弹体动态特性用简单的一阶模型来近似,不能反映直接力与气动力复合控制的特点。文献[8]通过早期的角度约束,应用滑模变结构控制方法设计了相应的导引律,适用于迎头拦截、尾追拦截和前向拦截。文献[9-11]设计了滑模导引律,文献[12-13]分别利用反馈线性化和动态逆的方法设计了三维导引律,文献[14]提出了圆周角导引的新概念,文献[15]提出了视线导引的方法。
为了更加符合临近空间拦截高速目标的实际需求,拦截导弹一般会采用直接力/气动力复合控制的方式[16-18]。文献[19]在准弹体系下建立模型,对采用直接力气动力复合控制导弹的控制系统进行了研究,采用扩张状态观测器对不确定性进行处理。文献[20]分析和简化了准弹体系下的模型,对采用双通道控制和单通道控制的姿控发动机的控制律分别进行了研究,实现了加速度的快速跟踪。
现有前向拦截导引律设计相关文献没有考虑直接力/气动力复合控制的动态特性与特点。由于对空中目标的拦截通常是发生在三维空间的,本文在考虑复合控制动态特性、特点和不确定性的基础上,对三维前向拦截导引律进行研究。
1 前向拦截制导数学模型
前向拦截示意图如图1所示[6],先将拦截导弹引向目标飞行轨道的前方,进而和目标沿同一方向飞行,要求拦截导弹的速度低于目标速度,拦截导弹通过尾部的导引头探测目标并做出相应的机动,使之始终保持在目标的飞行轨道上,当目标足够接近时,引爆战斗部或与之碰撞,彻底摧毁目标。
1.1 相对运动数学模型
假设导弹和目标的加速度矢量分别与它们各自的速度矢量垂直,即施加在导弹和目标上的加速度矢量仅改变其速度的方向而不改变速度的大小。
三维前向拦截的弹目运动几何关系如图2所示[4],I表示拦截导弹,T表示目标,r表示弹目相对距离。xiyizi是参考坐标系,与各轴对应的单位矢量分别为ii,ji,ki;xLyLzL是视线坐标系,与各轴对应的单位矢量分别为iL,jL,kL;xIyIzI是拦截导弹速度坐标系,与各轴对应的单位矢量分别为iI,jI,kI;xTyTzT是目标速度坐标系,与各轴对应的单位矢量分别为iT,jT,kT。φL和θL是惯性坐标系到视线坐标系转换的欧拉角,φI和θI是拦截导弹速度坐标系到视线坐标系转换的欧拉角,φT和θT是目标速度坐标系到视线坐标系转换的欧拉角。
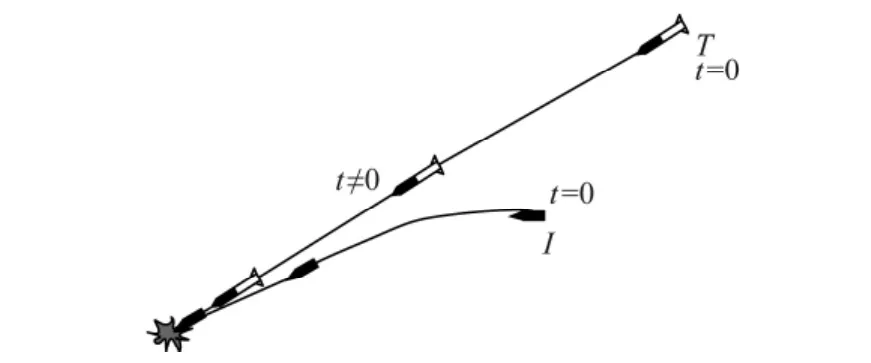
图1 前向追击拦截示意图
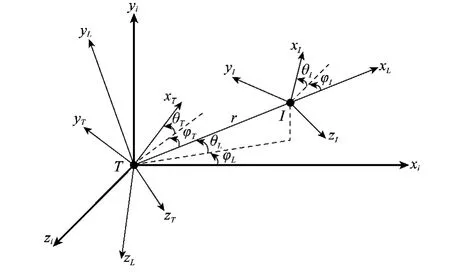
图2 三维拦截几何图
根据图2可得到导弹和目标相对运动方程如下:
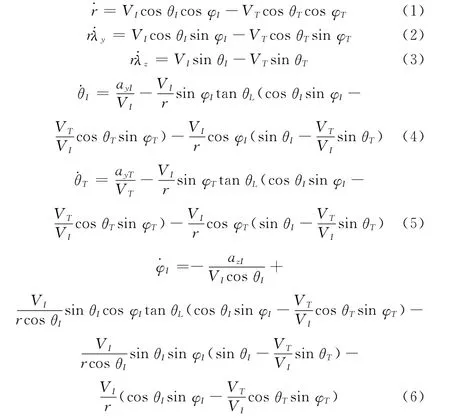
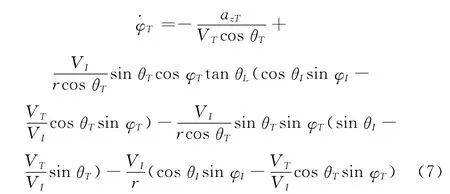
式中,VI和VT分别表示拦截导弹速度和目标速度和分别为视线角速率沿jL和kL的分量;ayI和azI分别为拦截导弹的俯仰加速度和偏航加速度;ayT和azT分别为目标的俯仰加速度和偏航加速度。
要想前向追击拦截到目标,在末制导的最后阶段,要求目标和拦截导弹的运动方向一致[4],即
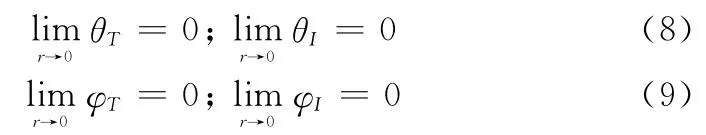
前向拦截导引的目标是把导弹导引到式(8)、式(9)满足的拦截点,因此,在设计过程中要求θI和θT、φI和φT保持如下比例关系[4]:

式中,N1和N2为导航系数。
1.2 导弹动力学模型
为了充分利用侧喷发动机,拦截导弹需要以一定的速度旋转,因此在准弹体系建立滚转导弹动力学模型[21],如图3所示[19],脉冲发动机是交错分布的,一共有10圈,每圈18个发动机。
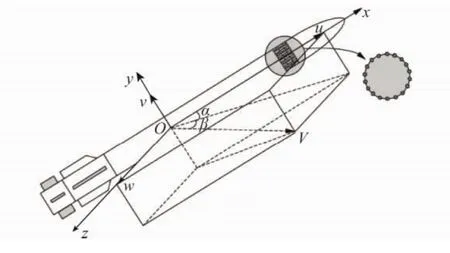
图3 姿控式复合控制自旋导弹配置示意图
假设弹体是轴对称形式并以一定角速度慢旋,导弹动力学模型为
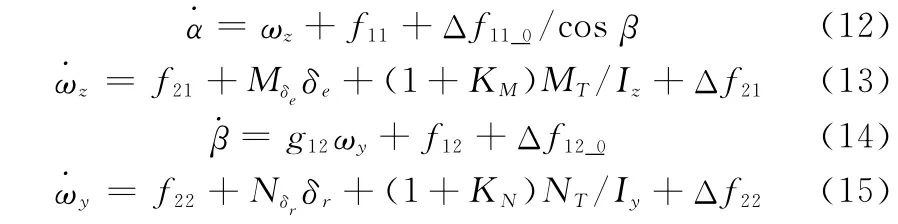
其中
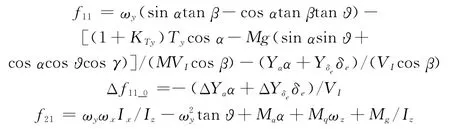
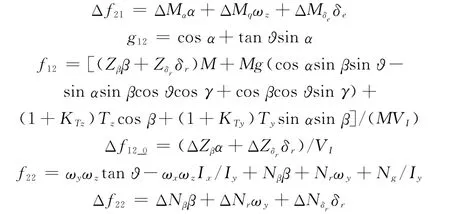
式中,M为拦截导弹质量;α为准弹体系下的攻角;β为准弹体系下的侧滑角;u、v、w分别为VI在准弹体系各轴的分量;Ix、Iy、Iz分别为在各轴方向转动惯量的分量;ωz、ωy、ωx分别为导弹角速度在准弹体系的分量;ϑ为俯仰角;Ty、Tz和NT、MT分别为直接侧向力和力矩在准弹体系的分量;KTy、KTz和KM、KN分别为喷流干扰力和干扰力矩放大因子;Ng、Mg为马格努斯力矩;Yα、Yδe、Zβ、Zδr、Nβ、Nr、Nδr、Mα、Mq、Mδe为动力学导数;ΔYα、ΔYδe、ΔZβ、ΔZδr、ΔNβ、ΔNr、ΔNδr、ΔMα、ΔMq、ΔMδe为动力学导数摄动;δe、δr为舵偏角在准弹体系的分量。
2 复合控制策略
采用直接力/气动力复合控制导弹的控制策略是在气动舵控制的基础上,先假设直接力是连续的并进行控制设计,然后对其进行离散化处理,得到离散直接力控制。
为简化控制设计,采用小角度线性化的思想,即假设α和β都是小角度,则式(12)~式(15)可转换为
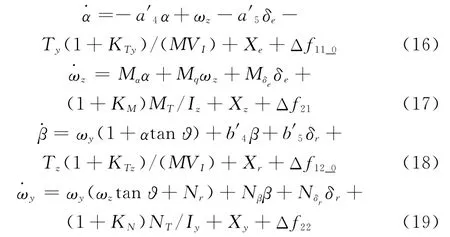
其中
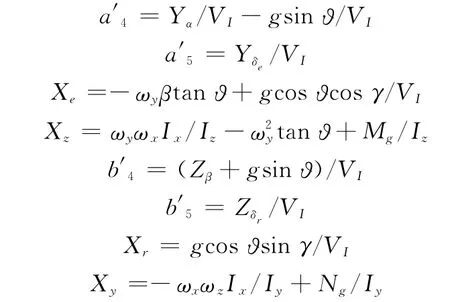
拦截导弹控制系统通常采用过载控制,加速度和角速度易于测量,而攻角α和侧滑角β一般难于测量。为了避免复合控制律中出现α和β,利用
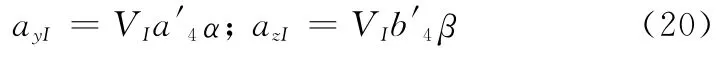
进行变换,并且假设气动舵采用如下控制规律(忽略舵机的动态):

得到含有气动舵反馈控制在内的导弹动力学模型
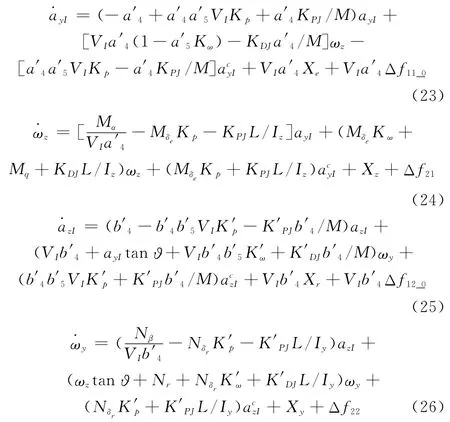
为简化控制设计,式(20)只考虑了气动力产生的过载,忽略了直接力和舵的影响。
假设俯仰通道和偏航通道的直接力是连续的,与舵控制系统类似,分别为T′y和T′z,控制规律取为

式中,KPJ、K′PJ和KDJ、K′DJ是比例系数和反馈系数。
式(27)、式(28)表示的直接力是连续信号,而实际的直接力是离散脉冲信号,需将连续直接力信号T′y和T′z进行离散化等效处理,得到可以实施的直接力信号Ty和Tz。
3 导引律设计
为了简化导引律的设计,将拦截导弹和目标的质点运动学与加速度动力学构成的动态系统,看成慢变子系统,将角速度动态子系统看成快变子系统。
3.1 慢变动力学的鲁棒动态逆设计
定义变量
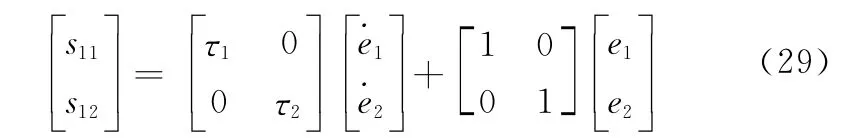
式中,τi(i=1,2)为比例系数,反映了当s1i=0时ei→0的快慢程度,且
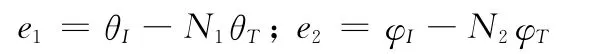
由式(29)知
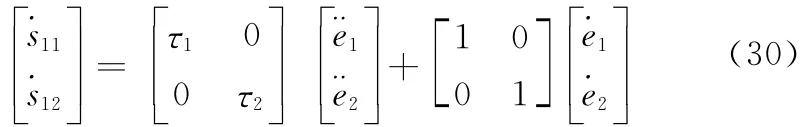
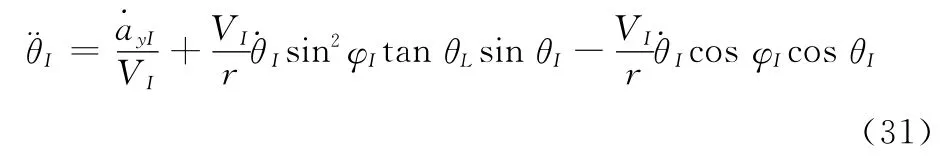
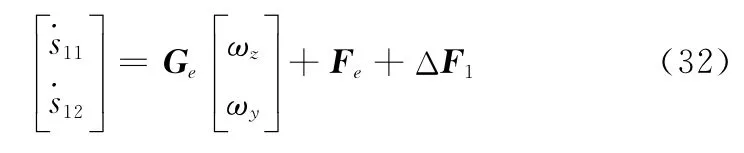
式中

其中
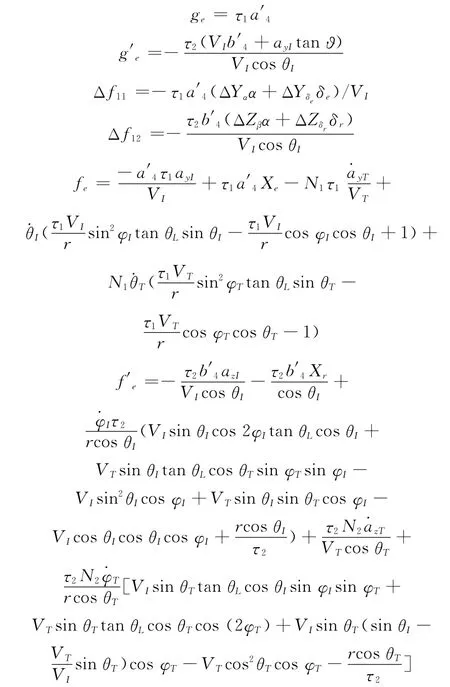
容易得到Δf1i(i=1,2)的界为
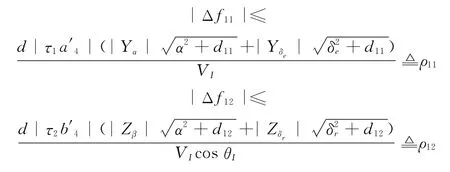
式中,d为气动参数的最大不确定性程度,其取值范围是0<d<1;d11和d12为很小的正数。进一步可以求出˙ρ11、˙ρ12。
取动态逆控制律为
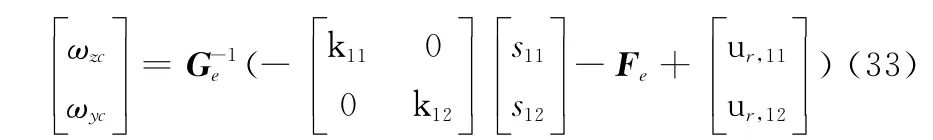
式中,k11、k12为慢变动力学子系统的带宽。取鲁棒控制项为
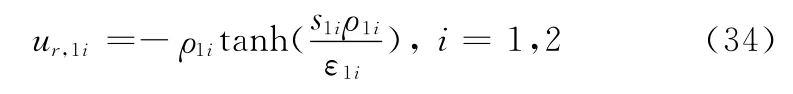
式中,ε1i为小的正数。
取慢变动力学子系统的李雅普诺夫函数为
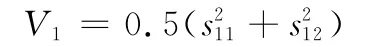
利用不等式[22]

可以证明
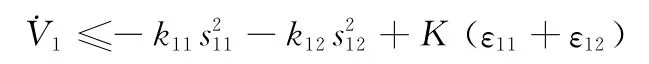
因此,慢变子系统是有界稳定的,适当选取k11、k12和ε11、ε12的值,可使s11、s12达到要求的精度。
式(33)为慢变动力学子系统的鲁棒动态逆控制律,其计算需要用到式(34)。
3.2 快变动力学的鲁棒动态逆设计
快变动力学子系统可写为
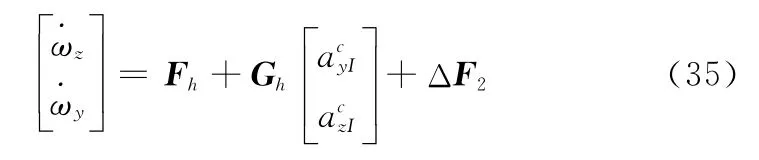
式中

其中

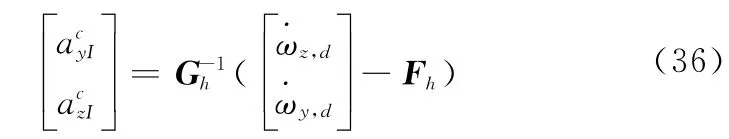
将式(36)代入式(35),得
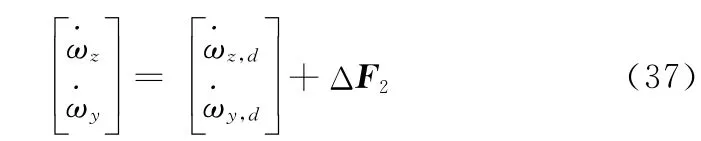
可以求得Δf2i(i=1,2)的界为
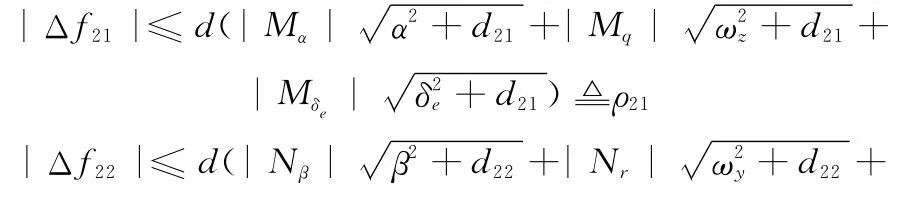
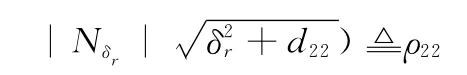
式中,d21和d22为很小的正数。
取快变动力学子系统的李雅普诺夫函数为
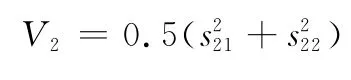
式中
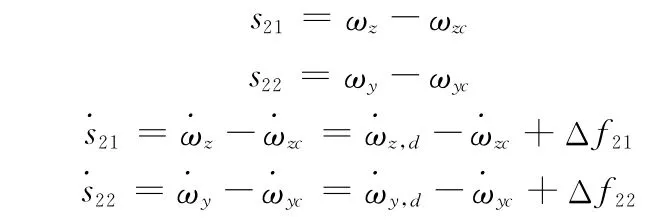
选取快变动力学子系统的鲁棒控制律为
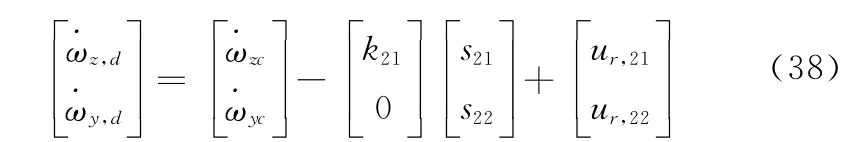
式中,k21、k22为快变动力学子系统的带宽。取鲁棒控制项为
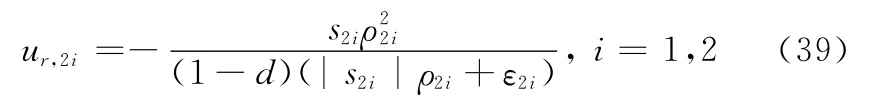
可以证明
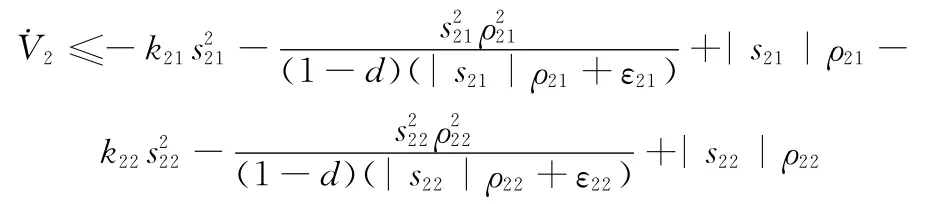
因此,快变动力学子系统是有界稳定的,适当选取k21、k22和ε21、ε22的值,可使s21和s22达到要求的精度。
式(36)为考虑复合控制系统动态特性和不确定性的前向拦截导引律,其计算需要用到式(38)、式(39)。
与二维平面情况不同的是,在三维空间情况下,有两种直接力控制方式可供选择:一种方式是同时对俯仰和偏航两个通道分别进行控制,即所谓的双通道控制方式,直接侧向力可通过将式(27)、式(28)离散化得到;另外一种方式是将俯仰和偏航两个通道的力合成后,采用单通道矢量控制方式。
将T′y和T′z合成,得到连续的合力为
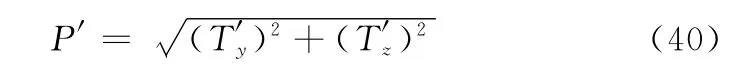
通过将P′进行离散化,得到离散直接力P。P与俯仰方向夹角为φ,定义如下:
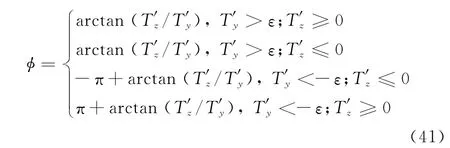
式中,ε为一比较小的正数,当|T′y|<ε时,则不用计算φ。
采用单通道控制时,考虑发动机侧喷的实际情况(弹体滚转和侧喷发动机的个数限制),某一周期当所需侧喷的方向上已没有侧喷发动机可用时,则不侧喷,等待下一个周期。
4 仿真验证
为验证方法的有效性进行如下仿真,假设在高空导弹能够产生的最大过载为4 g。目标的信息可以通过观测器、滤波等手段得到,这里假设目标的信息精确已知。
设目标速度为2 100m/s,某型拦截导弹的飞行速度为1 500m/s,弹体自旋速度为2.22πrad/s,导弹质量为140kg,转动惯量Iz=Iy=200kg·m2,Ix=180kg·m2,每个脉冲发动机的标称推力为2 000N,工作周期T=0.025s。
取气动系数Yα=4.192 5,Yδe=1.5,Mα=0.514 8,Mq=-0.025 7,Mδe=-8.083 5,Zβ=-0.027 9,Zδr=0.01,Nβ=0.514 8,Nr=-0.025 7,Nδr=-8.083 5。
为简单起见,这里取固定的Kp、Kω、KPJ、KDJ、K′p、K′ω值,即Kp=-0.003 9,Kω=0.160 4,K′p=-0.003 9,K′ω=
0.160 4,KPJ=0.035,KDJ=-0.315,K′PJ=0.035,K′DJ=-0.315。
假设喷流干扰力放大因子KTy=KTz=0.2,喷流干扰力矩放大因子KM=KN=0.3,气动参数向下拉偏40%。
目标初始位置为(-9 800m,36 000m,0m),拦截导弹初始位置为(9 000m,28 000m,1 000m),且θT、θI、φT、φI的初值分别是14°、35.5°、6°和18°。τ1=τ2=0.6,为确保直接力/气动力复合控制系统加速度慢变状态与角速度快变状态可分离,k11=k12=0.4,k21=k22=4,n1=n2=3。
实际工程应用时,可针对不同的特征点分别进行设计,然后进行插值处理。
对于采用单通道控制的拦截导弹,部分仿真结果如图4所示。图4(a)为θT和θI的变化曲线,图4(b)为φT和φI的变化曲线,它们全部单调收敛到0,满足式(8)、式(9)给出的前向拦截条件,保证了拦截导弹能够准确地拦截到目标。图4(c)反映了拦截导弹侧喷发动机的消耗情况,共消耗了90个。图4(d)为舵偏角变化曲线,当侧喷发动机工作时,舵偏角比较大。图4(e)为拦截导弹的攻角和侧滑角,直接力可以迅速建立起攻角和侧滑角。图4(f)为弹目运动轨迹,拦截导弹逐渐地运动到目标的前方,直到最后摧毁目标。
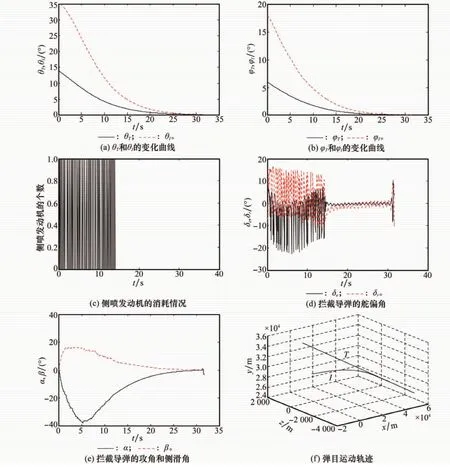
图4 单通道控制仿真结果
对于采用双通道控制的拦截导弹,部分仿真结果如图5所示。同双通道控制相比,控制效果比较相近。但是,采用双通道控制,俯仰通道发动机侧喷38个,偏航通道发动机侧喷76个,可见,采用单通道控制方式可以有效减少侧喷发动机的消耗。
如果不引入直接力控制,单纯采用气动舵进行控制,由于拦截导弹的过载响应比较缓慢,拦截导弹将无法命中目标,限于篇幅,不再给出仿真曲线。

图5 双通道控制仿真结果
5 结 论
对于采用直接力/气动力复合控制的导弹,为了充分利用侧喷发动机,导弹需要以一定的速度自旋,因此在准弹体系下建立导弹动力学模型进行研究。对动力学模型进行了线性化处理,在气动舵控制的基础上设计连续直接力,然后对其进行离散化处理,避免复杂的控制分配问题,便于前向拦截导引律设计时考虑复合控制的动态特性和特点。
对慢变动力学子系统和快变动力学子系统分别进行动态逆设计,应用李雅普诺夫稳定性理论的鲁棒控制方法对系统的不确定性进行处理,得到考虑复合控制系统动态特性及其不确定性的前向拦截三维导引律。
在考虑过载限制、气动参数的不确定性和喷流干扰的情况下对单通道控制和双通道控制分别进行了仿真研究。结果表明,直接侧向力能够迅速建立起攻角和侧滑角,所设计的导引律能够保证拦截导弹准确命中目标,并且,采用单通道控制方式可以有效减少发动机的消耗。如果单纯采用气动舵进行控制,所设计的导引律无法保证拦截导弹命中目标。说明了所设计导引律的正确性和鲁棒性。
[1]Golan O M,Shima T.Head pursuit guidance for hypervelocity interception[C]∥Proc.of the AIAA Guidance,Navigation and Control Conference and Exhibit,2004.
[2]Golan O M,Shima T.Precursor interceptor guidance using the sliding mode approach[C]∥Proc.of the AIAA Guidance,Navigation and Control Conference,2005.
[3]Zhao Z H,Shen Y,Liu H.A head pursuit guidance schemebased on variable structure control[J].Journal of Astronautics,2007,28(4):835-839.(赵振昊,沈毅,刘鹤.基于变结构控制的前向拦截导引方法[J].宇航学报,2007,28(4):835-839.)
[4]Ge L Z,Shen Y,Yuan L H.Three-dimensional guidance model and guidance law design for head pursuit interception[J].Systems Engineering and Electronics,2008,30(6):1118-1121.(葛连正,沈毅,院老虎.前向拦截的三维制导模型及制导律设计[J].系统工程与电子技术,2008,30(6):1118-1121.)
[5]Ge L Z,Shen Y.Head pursuit variable structure guidance law for three-dimensional space interception[J].Chinese Journal of Aeronautics,2008,21(3):247-251.
[6]Shima T.Head pursuit guidance[J].Journal of Guidance,Control and Dynamics,2007,30(5):1437-1444.
[7]Taub I,Shima T.Intercept angle missile guidance under timevarying acceleration bounds[J].Journal of Guidance Control and Dynamics,2013,36(3):686-699.
[8]Shima T.Intercept-angle guidance[J].Journal of Guidance Control and Dynamics,2011,34(2):484-492.
[9]Lum K Y,Xu J X,Abidi K.Sliding mode guidance law for delayed LOS rate measurement[C]∥Proc.of the AIAA Guidance,Navigation and Control Conference,2008.
[10]Shima T,Idan M,Golan O M.Sliding-mode control for integrated missile autopilot guidance[J].Journal of Guidance,Control and Dynamics,2006,29(2):250-260.
[11]Idan M,Shima T,Golan O M.Integrated sliding mode autopilot-guidance for dual-control missiles[J].Journal of Guidance,Control and Dynamics,2007,30(4):1081-1090.
[12]Srivastava R,Sarkar A K,Ghose D,et al.Nonlinear three dimensional composite guidance law based on feedback linearization[C]∥Proc.of the AIAA Guidance,Navigation and Control Conference,2004.
[13]Srivastava R,Prabhakar N,Sarkar A K,et al.Three dimensional nonlinear inverse dynamics guidance law for parallel navigation[C]∥Proc.of the AIAA Guidance,Navigation and Control Conference,2004.
[14]Tsalik R,Shima T.Inscribed angle guidance[C]∥Proc.of the AIAA Guidance,Navigation and Control Conference,2013.
[15]Ratnoo A,Shima T.Line-of-sight interceptor guidance for defending an aircraft[J].Journal of Guidance,Control and Dynamics,2011,34(2):522-532.
[16]Zimpfer D J,Shieh L S,Sunkel J.Redesigned pulse-widthmodulation spacecraft control[J].Journal of Guidance,Control and Dynamics,1998,21(4):529-534.
[17]Bernelli Z F,Mantegazza P,Nurzia V.Multi-pulse-width modulated control of linear systems[J].Journal of Guidance,Control and Dynamics,1998,21(1):64-70.
[18]Doman D B,Gamble B J,Ngo A D.Control allocation of reaction control jets and aerodynamic surfaces for entry vehicles[C]∥Proc.of the AIAA Guidance,Navigation and Control Conference,2007.
[19]Yao Y,Bi Y T.Design of blended control strategy for missiles with lateral jets and aerodynamic surfaces[J].Acta Aeronautica et Astronautica Sinica,2010,31(4):701-707.(姚郁,毕永涛.姿控式直接侧向力与气动力复合控制策略设计[J].航空学报,2010,31(4):701-707.)
[20]Ma K M,He F H.Control law design of lateral attitude jets for spinning missile[J].Acta Aeronautica et Astronautica Sinica,2009,30(10):1816-1822.(马克茂,贺风华.弹体自旋条件下姿控发动机控制律设计[J]航空学报,2009,30(10):1816-1822.)
[21]Qian X F,Lin R X,Zhao Y N.Missile flight dynamics[M].Beijing:Beijing Institute of Technology Press,2003.(钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2003.)
[22]Polycarpou M M.Stable adaptive neural network control scheme for nonlinear systems[J].IEEE Trans.on Automatic Control,1996,41:447-451.
E-mail:zhangya63@sina.com
吴华丽(1980-),通信作者,女,讲师,博士研究生,主要研究方向为导弹制导与控制。
E-mail:whl_yy@126.com
梁 勇(1976-),男,副教授,博士,主要研究方向为导弹制导与控制。E-mail:ytliangyong@sina.com
张金鹏(1964-),男,研究员,博士,主要研究方向为制导控制技术。E-mail:apeng-zhang@163.com
Three-dimensional head pursuit guidance law considering dynamic characteristics of uncertain hybrid control system
ZHANG You-an1,WU Hua-li1,LIANG Yong1,ZHANG Jin-peng2,3
(1.Department of Control Engineering,Naval Aeronautical and Astronautical University,Yantai 264001,China;2.China Airborne Missile Academy,Luoyang 471099,China;3.Luoyang Electro-Optics Technology Development Center,Luoyang 471099,China)
In order to intercept targets with high speed in high altitude accurately,a three-dimensional head pursuit guidance law considering uncertain dynamic characteristics for missiles with blended lateral jets and aerodynamic control is researched.The dynamics model of rotating missiles with blended lateral jets and aerodynamic control is simplified by linearization,and based on aerodynamic control,continuous lateral jets control is designed,and then it is discretized,which avoids the complicated control allocation problem.According to the kinematic model of three-dimensional head pursuit guidance and the dynamics linear model with uncertainties of missiles,the system is separated into a slow subsystem and a fast subsystem using time-scale separation,and the robust dynamic inversion controls of the slow subsystem and the fast subsystem are designed separately by applying the robust control method based on the Lyapunov stability theory.Thus,the three-dimensional head pursuit guidance law considering dynamic characteristics of the uncertain hybrid control system is obtained.The simulation of single channel control and double channels control are done to show the accuracy and effectiveness of the proposed method.
Lyapunov stability;blended lateral jets and aerodynamic control;head pursuit;three-dimensional guidance law;robust dynamic inversion
V 448.23
A
10.3969/j.issn.1001-506X.2015.06.20
张友安(1963-),男,教授,博士,主要研究方向为导弹制导与控制、先进控制理论。
1001-506X(2015)06-1354-08
2014-08-07;
2014-11-05;网络优先出版日期:2014-11-20。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20141120.2108.007.html
航空科学基金(20120184001)资助课题

