图像区域分割中的无监督图割方法

赵 婕，谢 刚

（1．太原理工大学信息工程学院，山西太原030024；2．太原大学计算机工程系，山西太原030032）

图像区域分割中的无监督图割方法

赵 婕1，2，谢 刚1

（1．太原理工大学信息工程学院，山西太原030024；2．太原大学计算机工程系，山西太原030032）

提出一种基于图割算法的图像多区域分割方法，该方法采用核函数对数据项进行隐性的非线性映射，将原始数据映射到高维特征空间，实现图像的线性多类划分，扩展了分段常数模型的应用范围，提高了复杂区域的分割效果。由于图像边缘梯度变化剧烈，具有不连续性，在平滑项中加入图像的梯度约束条件，减少过分割。同时，采用无监督方法设置初始参数，避免了交互操作，更符合多区域分割的要求。实验结果表明，新方法不受图像内容的限制，无论是主观视觉判断还是客观定量分析，该方法都具有较好的分割效果。

区域分割；图割算法；核方法；边缘梯度

0 引 言

图像在人眼中是由不同目标、不同区域联合构成，人们通过辨识图像中包含的各个目标，可以快速、准确地理解其所包含的信息。但是对于计算机而言，这个过程极具挑战性。图像分割就是帮助计算机像人眼一样，实现目标提取与识别、图像理解以及场景恢复等功能的前期环节，是图像分析与理解的基础技术［1］。图像分割一直以来是计算机视觉领域的研究热点，而图像的多区域分割是图像分割中最为关注的研究方向，广大研究者努力寻找更准确、更高效的多区域分割方法。由于能量函数模型具有统一的分割框架以及可以使用标准优化方法求解的优点，并且通过贝叶斯统计可以证明将图像分割问题转换为求解能量函数最优解的正确性，能量优化方法成为研究图像分割的一个新流派［2－3］。

图割算法是一种以图论为理论基础的优化方法，可用于优化能量函数全局解，而图像中的像素点又可以与网络图的节点对应，图论的相关理论与方法适用于图像分析与处理领域的研究。因此，图割算法成为近年来广大学者研究图像分割的重要方法。2000年，加拿大西安大略大学Boykov等人［4］首次将图割算法引入图像分割领域，经过数学证明验证了求解离散能量函数的全局最优解与图像的目标分割过程等效，并且使用交互式方法，通过求解能量函数最优解在实际应用中实现了目标与背景的分割。但是，当能量函数是非凸函数时，无法精确获得全局最优解。2002年，美国康奈尔大学Kolmogorov等人［5］提出一种求解具有较强约束的局部最优解的图割算法，用特定的局部最优解替代全局最优解，实验证明了该算法的有效性，并成功地应用于多镜头3D场景重建。经典图割算法适用于灰度图像，2004年，英国微软剑桥研究院Rother等人［6］提出GrabCut算法，用高斯混合模型代替单色直方图模型，将图割算法扩展到彩色图像的目标分割；同时，用户只需提供左上角和右下角两个点，便可形成一个覆盖目标的矩形框，简化了交互操作。研究者们还在能量函数中融入各种先验信息，以提高图割算法的图像分割效率。2010年，西安大略大学Veksler［7］将星形作为通用的目标形状，以先验知识的形式融入能量函数的结构中，用户只需提供目标的中心点就可以准确分割出目标，提高了图像中目标的分割效果。在近十几年中，图割算法得到了广大研究者的关注，针对算法流程的设计与能量函数的构造不断地提出改进方法［8－11］，促进了图像分析与处理研究的发展与进步，尤其是在图像分割领域。

图割算法在图像分割领域的使用范围主要集中于目标分割和交互式操作。这里指的目标分割是将图像中的目标从背景中有效地分割出来，即图像被分为两个区域（目标和背景），属于二分类。用户预先确定一定量的目标像素和背景像素，通过交互式操作完成图割算法中参数的初始化设置。图割算法在交互式的两区域分割研究中已经取得了很好的效果［4－11］。但是，由于图像的复杂性，实际图像都是由多个区域组成，如何将图像有效分割成多个具有特定性质的区域，更具有实际应用价值，同时也更具有挑战性。图像的多区域分割成为图割算法目前以及未来研究的重点与难点。对于图像的多区域分割，如果仍然使用交互式操作完成初始化设置，那么图像越复杂，分割的区域越多，交互式操作也越困难。因此，交互式操作不适合图像的多区域分割。

图割算法应用到图像的多区域分割时，当分割区域大于3个以上，能量函数的全局优化成为NP－hard问题，通常采用α－扩展、α－β交换等近似优化方法［12］。能量函数模型的构建是决定图割算法处理图像能力的关键因素，针对近似优化方法，研究者们提出一些新的能量函数模型。文献［13］提出一种离散能量函数模型，加入标签惩罚限制使用标签的数量，通过能量平衡解决经典优化问题中的无容量限制的设施选址问题（uncapacitated facility location problem，UFLP），经过实验验证了该模型的有效性。文献［14］构造了评价标签质量的多模型能量函数，包括测量模型相似程度的相似项和测量证明模型合理的证据数量的模型惩罚项两部分。采用一种快速的融合移动方法实现多模型能量函数的优化，将融合问题变换为最小加权点覆盖问题，该方法具有近邻传播一样的鲁棒性。文献［15］通过t－权重将多个形状先验信息引入能量函数构造的图中，形状距离是对称的，同时还符合三角不等式定理，采用多阶段图割算法完成有重叠的多目标分割。这些能量函数模型的提出推进了图割算法在多区域分割中的应用，但是仍然存在一些缺点有待改进，例如模型复杂、计算量大，分割效果与分割区域的数量有关，并且分割区域的数量需要人为指定等问题。

本文将核方法与边缘梯度信息有机融合，提出一种无监督图割方法。首先，采用常数模型描述各个划分区域内的图像数据，将图像数据映射到高维空间，实现复杂图像数据的线性可分，统计模型简单、计算量小，并且提高了复杂区域的分割效果。其次，在多标签分配过程中，加入梯度约束条件以保持边缘不连续性，减少过分割。最后，参数初始化设置避免了交互操作，通过少量样本测试便可以确定合适的参数值，完成多区域的自动分割。

1 无监督图割方法的基本步骤

图像多区域分割中应用图割算法的核心思想是构建一个能够体现图像特征的能量函数，对能量函数的最优化求解，完成各个区域的标签分配。每一个分割区域可以看作一类数据，每一类图像数据都有唯一的标签与之对应，通过解决标签分配问题实现图像数据的空间聚类。无监督图割方法避免了交互式操作，主要包含有以下3个基本步骤：

步骤1 构造无监督图割的能量函数

设I表示一幅图像，P为该图像中所有像素的集合，将图像I分割为Nseg个区域，对于任意像素p，则存在一个对应函数f（p）表示像素点p的分类标签，即

式中，L是标签类别的集合，其基数小于等于Nseg。标签类别为l（l∈L）的所有像素构成一个划分区域Rl，即

通常能量函数由数据约束和平滑约束两个特征项之和组成

这两个约束项中包含图像分割所需的图像特征，其中EData（f）是数据约束项，衡量分割区域中图像数据和统计模型的一致性程度。采用分段常数模型［13］（piecewise constant model，PCM）作为统计模型描述划分区域内像素的特征。PCM中同一区域内图像特征近似等同，不同区域内图像特征差异较大，每个区域内的像素分配统一的标签，用相同的图像特征进行表示，适用于图像的多区域分割，并且计算量小。

式中，μl为区域Rl的PCM参数；Ip表示像素p的图像特征。

但是，在实际应用中图像数据分布复杂，而PCM要求图像数据按照线性分布，大大限制了其应用范围。为了扩展PCM在实践中的应用范围，采用核映射方法［16－18］对非线性可分的图像数据进行隐性的非线性映射，将原始数据映射到高维特征空间，实现线性可分的目的。

ESmooth（f）是平滑约束项，用来描述分割区域的光滑程度，融入梯度变化作为约束条件，体现出分割区域内光滑连续而区域边缘不连续的特性。

式中，λ为比例系数，用来调节数据约束和平滑约束两个特征项所占的比重；N表示像素邻域。

步骤2 构建加权图

根据构造的能量函数可以构建一个加权图，设图G＝〈v，ε〉，其中v是图中的顶点，包括图像中的所有像素点p∈P，以及用于表示标签类别的额外端点l∈L。ε是图中的边，也相应地包括两部分：相邻像素点之间的边和像素点与额外端点之间的边。边的权重如表1所示。

表1 边的权重分配

步骤3 基于图割的近似优化实现多区域分割

采用α－β交换的最大流／最小割算法［12］迭代进行能量函数的近似最优化，实现图像的多区域分割。

本文提出的无监督图割方法，本质上是一种融合核方法与边缘梯度变化的多目标自动分割方法。该方法的关键在于能量函数的构造和参数初始化设置，后面的第2节和第3节对这两部分内容分别做详细介绍。

2 能量函数的构造

2．1 数据项在核空间的转换及计算

为了使PCM符合实际应用要求，采用核方法对非线性可分的图像数据进行隐性的非线性映射，将原始数据映射到高维特征空间，实现线性可分的目的。这里“隐性”是指，不必明确给出非线性映射函数φ（·）的具体表达形式，内积运算可以用核函数代替［19］，即K（x，y）＝φ（x）·φ（y）。因此，在经典图割算法中引入核方法，既可以使PCM成为有效描述图像数据的通用的简单模型，也可以充分利用基于图割的能量优化方法，同时还体现了线性方法便于处理、计算简单的优点，有效实现图像的同质多区域分割，此方法适用范围广泛，不受图像类型的限制。

将数据项通过非线性映射函数φ（·）映射到核空间，则数据项转换后的计算公式为

设K（·）为选用的核函数，定义

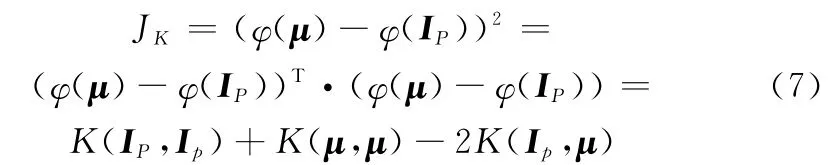
将式（7）代入式（6），数据项的核空间转换公式简化为

转换到核空间的数据项，不必考虑映射函数φ（·），只要确定使用的核函数即可完成数据项的计算。本文采用径向基函数（radial basis function，RBF）中的拉普拉斯核函数（Laplace kernel，LRBF），该核函数在数据聚类中具有优势，且受参数影响较小，适合于区域分割。LRBF核函数的公式如下：

2．2 融合边缘梯度约束的平滑项计算

边缘信息是划分图像不同区域的重要特征。平滑项的作用是描述图像分割区域的光滑程度，为使分割达到更好的效果，在平滑项中考虑图像的边缘信息，可以减少多区域分割产生的过分割。由于梯度特征在图像边缘变化剧烈，梯度变化可以作为判定图像边缘的基本准则。将图像中边缘梯度变化作为约束条件融入平滑项，可以保持边缘的不连续性，提高区域边缘分割的准确性，同时降低过分割现象的出现。则融合梯度约束的平滑项定义为

式中，Bpq为相邻两像素点的边缘梯度约束。设Gp和Gq分别表示像素p和像素q的梯度，则

式中，σ是梯度变化阈值，其值取分割区域内的梯度方差。因为统计模型采用PCM，Bpq的值由常数C决定，实验中C取值为5。

从平滑项公式可以看出，像素p和q划分在不同区域时，需要确定边缘不连续性。如果像素p和q梯度差异较大时，表明两个像素处于区域边缘，那么Bpq的值越小，平滑项确定的能量也越小，则像素p和q被分割可能性越大，可以保持边缘的不连续性。如果像素p和q梯度差异较小时，Bpq的值增大，像素p和q被分割可能性减小，减少过分割现象。

3 多区域标签初始分配与模型参数计算

统计图像的颜色特征，用直方图描述统计量，对于任意级值i，如果H（i）≥H（i±1），则H（i）是峰值。设置K均值聚类的个数为峰值数n，即区域标签个数为n。特征值与峰值最接近的像素点设为聚类初始中心。利用确定的中心点和聚类个数，对图像数据进行K均值聚类，每一个聚类结果成为一个分割区域，为各个区域分配初始标签。聚类个数n与颜色直方图组距h有关，n与h成反比，经过实验验证，h的取值范围为［10，20］。

计算每个分割区域Rl（l∈L）的PCM参数μl。首先，μl的初始值为区域Rl内所有像素颜色特征的均值，用μlo表示。当采用α－β交换算法迭代逼近能量函数最优解时，在每次迭代过程中，区域标签都会重新分配，μl值也会发生改变。μl的计算公式如下：

式中，m表示迭代次数，即μlm为第m次迭代时PCM参数μl的值。

4 实验结果与分析

Berkeley图像库是经典的测试图像分割效果的数据库，其中还包含了人工标准分割结果。本文选用该图像库中的10幅图像作为训练图像，用于无监督图割方法中参数的选择实验；选用300幅图像做多区域分割效果测试实验。实验的硬件环境为双核CPU T2390 1．8GHz，内存2G；软件环境为Matlab R2011a开发平台。

4．1 平滑项比例系数λ选择与测试分析

平滑项比例系数λ的取值对图像多区域分割的效果有较大的影响，下面具体讨论λ的取值原则。

图1 λ的选择分析

λ表示在能量函数中平滑项与数据项的比例。λ的值不同，平滑项相对于数据项占有的比例不同，图像多区域分割的效果也会不同。依据分割效果的视觉直观判断，选择合适的λ值。以Berkeley库中图12003为例，λ的选择分析过程如图1所示。如果λ很小，则平滑约束项占有的比重很小，此时主要考虑数据项对能量函数的影响，忽略了平滑项，数据项的约束使图像中同质区域都被有效分割，但是由于缺少了平滑项中边缘梯度约束，分割区域较小且零散，过分割现象严重，不利于后续的图像分析与理解。如果λ增大，则平滑项中边缘梯度约束的作用加大，过分割现象逐渐减小，多区域分割效果好。但是λ增大到一定程度，平滑项的占有率远远大于数据项时，虽然过分割现象消失，但是图像中有些区域不能被分割出来。经过实验测试，λ取值在［2，3］范围内，无监督图割方法的分割效果最好。

4．2 与其他分割方法的比较

通过图像训练测试，选择好合适的参数之后，进行多区域分割效果比较实验。将本文提出的方法与聚类结果融合法［20］（fusion of clustering results，FCR）、归一化分割法［21］（normalized cuts，Ncuts）等经典多区域分割方法进行比较。3种分割方法的区域分割效果如图2所示，由于篇幅有限，仅展示了Berkeley库中一部分的图像分割结果。以图2中的分割效果为例，对3种方法进行分析比较。

FCR是一种聚类结果融合方法，采用非稳定的马尔可夫随机场（Markov rank field，MRF）模型实现6个颜色空间特征聚类结果的融合。由于包含了6个颜色空间中的纹元特征和candy边缘特征，并进行边缘的软分割，图像误分割现象较少，但是过分割现象严重。例如，图67079中建筑的屋顶、图296059中大象的脊背轮廓和图187029中孩子的头顶都出现了双边缘分割线。

Ncuts是基于图论的归一化分割算法，由于归一化处理，减少了分割结果中的单一孤立分割点，因而分割区域形状紧凑。Ncuts方法可以控制分割区域的数量，而分割区域总数较小（＜5）时，分割效果不理想，本文选用的分割区域数量为20。图2的分割效果显示Ncuts方法分割所得区域面积大致相近，多区域分割结果基本准确，但是边缘分割线波动较大，影响了分割精度。例如，图295087中树枝的边缘线和图67079中石柱的边缘线都有较大跳变，与标准分割线有明显的差别。

本文提出的方法将数据项映射到核空间，实现复杂数据的线性可分，模型简单通用，计算复杂度低，而区域分割效果较好，尤其是低维空间中分割复杂的区域。例如，图295087上石头中间的两个空洞和图296059中右边大象嘴下方的天空和草地等区域处于全包围状态，属于复杂的分割区域。本文提出的方法对这些区域的分割效果比其他方法要好。同时，由于融合了边缘梯度约束，过分割现象也得到抑制，并且边缘分割线也较为流畅连贯。因此，从视觉效果直观判断，本文提出的方法分割效果更为理想。

下面采用概率Rand指数（probabilistic rand index，PRI）、信息变化指数（variation of information，VoI）和边界偏离误差（boundary displacement error，BDE）3个评价指标，客观定量地评价3种方法的分割效果。PRI指标的作用是判断算法分割结果与标准分割的相同程度，取值范围在0～1之间，该指标值越大表示算法分割结果越接近标准分割，分割效果越好。VoI是信息变化指数，其值域为非负实数，用条件熵描述算法分割结果不能被标准分割结果解释的随机性，该指标越小分割效果越好。BDE指标通过计算区域边缘精度来判定分割效果，取值范围是［0，∞），取值越小表示边缘偏离误差越小，分割效果越好。

图2 3种区域分割方法图像分割效果比较

采用本文提出的方法对Berkeley库中300幅图像进行区域分割，统计PRI指标的分布情况如图3所示。PRI指标高于0．8的图像数量超出整个图像库的四分之三，表明本方法适用范围广泛，分割效果不受图像内容限制。为了进一步验证本文方法的分割效果，将本文方法与其他两种典型的多区域分割方法作量化比较。标准分割和3种分割算法的定量评价指标如表2所示，表中各指标的值是测试Berkeley库中300幅图的平均值。通过定量分析，表明本文提出的方法优于另外两种方法。

图3 Berkeley库中300幅图像的PRI指标统计

表2 定量评价指标

通过实验证明，本文提出的方法不论是主观视觉判断还是客观定量分析，都具有较好的分割效果，表明了该方法在图像多区域分割中的有效性。

5 结束语

本文提出一种融合了核方法与边缘梯度信息的无监督图割算法，通过图像数据向高维特征空间的映射，扩展了分段常数模型的实际使用范围，实现了复杂图像数据的线性可分，既提高了区域分割效果又降低了计算量。同时，在平滑项中加入边缘梯度信息，增加了边缘的划分精度，减少了过分割的出现，进一步提高区域分割性能。经实验定性定量分析，该方法具有较好的多区域分割效果，也符合多区域分割的实际要求。本文提出的多区域分割方法可以较好地解决图像中多目标自动分割问题，为后面的多目标识别、语义标注、场景理解等研究奠定了良好的基础。

［1］Carreira J，Sminchisescu C．CPMC：automatic object segmentation using constrained parametric min－cuts［J］．IEEE Trans．on Pattern Analysis and Machine Intelligence，2012，34（7）：1312－1328．

［2］Kappes J H，Andres B，Hamprecht F A，et al．A comparative study of modern inference techniques for discrete energy minimization problems［C］∥Proc．of the IEEE Conference on Computer Vision and Pattern Recognition，2013：1328－1355．

［3］Liu G，Zhou Z，Xie S．Global minimization of adaptive local image fitting energy for image segmentation［J］．Journal of Systems Engineering and Electronics，2014，25（2）：307－313．

［4］Boykov Y，Jolly M P．Interactive organ segmentation using graph cuts［C］∥Proc．of the 3rd International Conference on Medical Image Computing and Computer－Assisted Interven－tion，2000：276－286．

［5］Kolmogorov V，Zabih R．Multi－camera scene reconstruction via graph cuts［J］．Lecture Notes in Computer Science，2002，2352：82－96．

［6］Rother C，Kolmogorov V，Blake A．“GrabCut”－interactive foreground extraction using iterated graph cuts［J］．ACM Trans．on Graphics，2004，23（3）：309－314．

［7］Veksler O．Star shape prior for graph－cut image segmentation［J］．Lecture Notes in Computer Science，2008，5304：454－467．

［8］Wang B，Li J，Gao X B．An edge－and region－based level set method with shape priors for image segmentation［J］．Chinese Journal of Computers，2012，35（5）：1067－1072．（王斌，李洁，高新波．一种基于边缘与区域信息的先验水平集图像分割方法［J］．计算机学报，2012，35（5）：1067－1072．）

［9］Liu S T，Wang H L，Yin F L．Interactive ship infrared image segmentation method based on graph cut and fuzzy connectedness［J］．Acta Automatic Sinica，2012，38（11）：1735－1750．（刘松涛，王慧丽，殷福亮．基于图割和模糊连接度的交互式舰船红外图像分割方法［J］．自动化学报，2012，38（11）：1735－1750．）

［10］Chang J C，Chou T．Iterative graph cuts for image segmentation with a nonlinear statistical shape prior［J］．Journal of Mathematical Imaging and Vision，2014，49（1）：87－97．

［11］Wang H，Zhang H，Ray N．Adaptive shape prior in graph cut image segmentation［J］．Pattern Recognition，2013，46（5）：1409－1414．

［12］Boykov Y，Veksler O，Zabih R．Fast approximate energy minimization via graph cuts［J］．IEEE Trans．on Pattern Analysis and Machine Intelligence，2001，23（11）：1222－1239．

［13］Delong A，Osokin A，Isack H N，et al．Fast approximate energy minimization with label costs［J］．International Journal of Computer Vision，2012，96（1）：1－27．

［14］Delong A，Veksler O，Boykov Y．Fast fusion moves for multi－model estimation［C］∥Proc．of the 12th European Conference on Computer Vision，2012：370－384．

［15］Vu N，Manjunath B S．Shape prior segmentation of multiple objects with graph cuts［C］∥Proc．of the IEEE Conference on Computer Vision and Pattern Recognition，2008．

［16］Dhillon I S，Guan Y，Kulis B．Kernel K－means，spectral clustering and normalized cuts［C］∥Proc．of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2004：551－556．

［17］Kulis B，Basu S，Dhillon I S，et al．Semi－supervised graph clustering：a kernel approach［J］．Machine Learning，2009，74（1）：1－22．

［18］Dhillon I S，Guan Y，Kulis B．Weighted graph cuts without eigenvectors：a multilevel approach［J］．IEEE Trans．on Pattern Analysis and Machine Intelligence，2007，29（11）：1944－1957．

［19］Salah M B，Mitiche A，Ayed I B．Multiregion image segmentation by parametric kernel graph cuts［J］．IEEE Trans．on Image Processing，2011，20（2）：545－557．

［20］Mignotte M．Segmentation by fusion of histogram－based K－means clusters in different color spaces［J］．IEEE Trans．on Image Processing，2008，17（5）：780－787．

［21］Shi J，Malik J．Normalized cuts and image segmentation［J］．IEEE Trans．on Pattern Analysis and Machine Intelligence，2000，22（8）：888－905．

E－mail：tydxcomputer＠163．com

谢 刚（1972－），通信作者，男，教授，博士，主要研究方向为智能信息处理、智能控制。

E－mail：xiegang＠tyut．edu．cn

Unsupervised graph cuts for image region segmentation

ZHAO Jie1，2，XIE Gang1
（1．College of Information Engineering，Taiyuan University of Technology，Taiyuan 030024，China；2．Department of Computer Engineering，Taiyuan University，Taiyuan 030032，China）

A multi－region image segmentation method based on graph cuts is proposed．Original image data is transformed into high－dimension feature space via the implicit nonlinear mapping of data term by kernel function，so that the effect of segmentation is improved，multi－class partition of the image is achieved and the application of the piecewise constant model is extended．Due to the edge gradient of the image dramatically changes with discontinuity，the gradient constraint is introduced to smooth terms in order to reduce the over segmentation．Simultaneously，initial parameters are set by the unsupervised method without user interactions to meet the requirements of multi－region segmentation．Experiment results show that the proposed method is not restricted by the content of the image and has better segmentation results through both the subjective visual judgement and the quantitative analysis．

region segmentation；graph cuts；kernel method；edge gradient

TP 391

A

10．3969／j．issn．1001－506X．2015．06．31

赵 婕（1978－），女，讲师，博士研究生，主要研究方向为图像处理、分析与理解、模式识别与机器学习。

1001－506X（2015）06－1431－06

2014－07－07；

2014－10－10；网络优先出版日期：2014－11－20。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141120．1831．004．html

太原市科技项目人才专项基金（12024728）资助课题