Attitude Control of Multiple Rigid Bodies with Uncertainties and Disturbances

Yuanqing Xia,Ning Zhou,Kunfeng Lu,and Yong Li

Attitude Control of Multiple Rigid Bodies with Uncertainties and Disturbances

Yuanqing Xia,Ning Zhou,Kunfeng Lu,and Yong Li

—Decentralized attitude synchronization and tracking controlfor multiple rigid bodies are investigated in this paper.In the presence of inertia uncertainties and environmental disturbances,we propose a class of decentralized adaptive sliding mode control laws.An adaptive control strategy is adopted to reject the uncertainties and disturbances.Using the Lyapunov approach and graph theory,it is shown that the controllaws can guarantee a group of rigid bodies to track the desired time-varying attitude and angular velocity while maintaining attitude synchronization with other rigid bodies in the formation.Simulation examples are provided to illustrate the feasibility and advantage of the control algorithm.

Index Terms—Attitude control,attitude synchronization,sliding mode control(SMC),adaptive control.

I.INTRODUCTION

D Uring the past decades,the attitude synchronization of rigid bodies(spacecraft)has attracted a great deal of attention.Many techniques and results have been proposed in this research field and these can be classified as leader follower[1−4],virtual structure[5−6],behaviorbased[7−8],and graph-theoretical approach[9−13].Especially, the graph-theoretical approach has been introduced to study the cooperative control of multi-agent system using limited local interaction[14]and also has been applied to attitude synchronization[10],but most of the results under the assumption that the communication links are undirected i.e., bidirectional.In the practical application,the communication topology may be directed,such as in unidirectional satellite laser communication system.Furthermore,compared with the undirected communication topology,the control problem of attitude synchronization under directed communication topology is more challenging.

It is well known that the attitude dynamics of rigid body is coupled and highly nonlinear,which is the main obstruction to design a high precision attitude control law.Many nonlinear control methods have been employed to improve the closed-loop performances recent years,such as optimalcontrol,sliding mode control,adaptive control,etc.As the sliding mode control(SMC)is an effi cient control technique which is competent for systems with profound nonlinearity and modeling uncertainty,it has been applied in many previous works to rigid body attitude control problem[15−16]. The adaptive control is also a valid method to overcome the parametric uncertainty.An adaptive attitude control law was designed by Chen and Huang to enhance the ability of disturbance rejection of the closed-loop system[17].With the combination of the sliding mode controland adaptive control, Wu and Wang proposed a decentralized adaptive sliding mode control law to ensure that the multispacecraft sliding-mode surface were reached asymptotically,then the attitude error and angular velocity error of each spacecraftconverged to zero asymptotically[1−8].

In this paper,we consider the attitude synchronization and tracking problems for multiple rigid bodies.First of all,a sliding-mode vector is designed with two parameters for attitude tracking and attitude synchronization,which may allow the designer to prioritize between station-keeping behavior and formation-keeping behavior.As the inertia uncertainties and environmental disturbances are assumed to be bounded with unknown constants,an adaptive control strategy is introduced to reject them.Two decentralized control laws are proposed to ensure thateach rigid body attains the desired time-varying attitude and angular velocity while maintaining attitude synchronization with other rigid bodies in the formation.In the proposed controllaws,the information flow among rigid bodies includes the absolute inertial attitude and angular velocity, the desired attitude and angular velocity,and controlinput,as wellas the nominalinertia matrix.Each rigid body also needs to know its own information.In the singular rigid body attitude control,itdoes notconsider the synchronization problem,and its own information is enough for the control law design.

The organization of this paper is as follows.In Section II, based on unit quaternion,the rigid body attitude kinematics and dynamics equations are derived.Furthermore,the preliminary notions in graph theory,lemmas and control objective are assembled.In Section III,a decentralized sliding mode control strategy is proposed;also the convergence analysis of the resulting closed-loop system is performed.In Section IV,the modified control scheme is proposed to alleviate the chattering phenomenon.Simulation examples are provided to illustrate the feasibility and superiority of the controlalgorithm in Section V.Finally,conclusion and future work are given in Section VI.

II.PROBLEM STATEMENT

A.Rigid Body Attitude Kinematics and Dynamics

In this paper,the attitude of each rigid body is represented by the unitquaternion representation withoutsingularities.Theattitude kinematics and dynamics of each rigid body in terms of the unit quaternion are given by

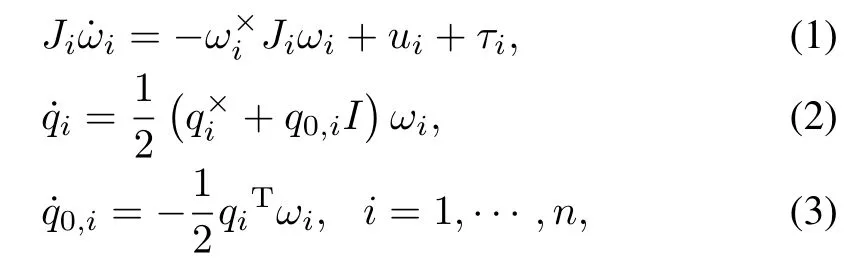
where Ji=JTidenotes a positive definite inertia matrix of the i th rigid body.I∈R3×3is the identity matrix.ωi∈R3denotes the body angular velocity of the i th rigid body with respectto the inertialframe expressed in the body frame ofthe i th rigid body.ui∈R3denotes the control torque.τi∈R3denotes the disturbance torque.qi∈R3and q0,i∈R are the vector partand scalar part of the unitquaternion thatrepresent orientation of the body-fixed frame with respectto the inertial frame.The notation x×for any vector x=£x1x2x3⁄T∈R3is used to denote the skew-symmetric matrix:

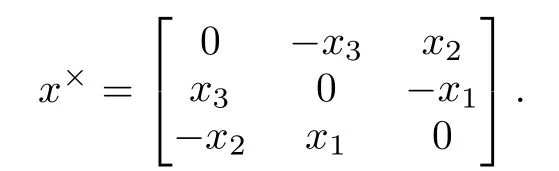
In the case of tracking a desired rotationalmotion,the problem formulation is similar to that in the related work[18].The desired rotational motion of the i th rigid body is described by the attitude motion of a frame D,whose orientation with respectto the inertialframe is specified by the unitquaternion (ξi,ξ0,i)∈R3×R that is subject to the constraintξTiξi+ξ20,i=1.ωdi=ωdi(t)∈R3is the desired angular velocity of the i th rigid body with respect to frame D.

The related assumptions aboutthe dynamics of the attitude synchronization and tracking systems are given as follows, which will be used in the further analysis in Sections III and IV.

Assumption 1.Denote Ji= ¯Ji+ ˜Ji,where¯Jiand˜Jiare the nominal part and uncertain part of the inertia matrix of the i th rigid body,respectively.It is assumed that the inertia matrix uncertainties are bounded and satisfy‖˜Ji‖≤Δi.

Assumption 2.All the environmental disturbances due to gravitation,solar radiation pressure,magnetic forces and aerodynamic drag are assumed to be bounded.Thus,the external disturbances are assumed to satisfy‖τi‖≤¯τi.

Assumption 3[19].The control law of each rigid body might use its neighbors'angular velocity errors and error quaternions in the cooperative attitude control problem,and error quaternion is bounded from its definition.Thus,the control torque uiis assumed to satisfy

whereΔi,¯τiandζi,jare unknown nonnegative constants for i=1,···,n,j=0,1,2,Nirepresents the i th rigid body and all the rigid bodies with which the i th rigid body can communicate,and‖·‖denotes the standard Euclidean vector norm or induced matrix norm,as appropriate.

Assumption 4.There exist two constants¯ω1＞0 and¯ω2＞0 such that‖ωdi(t)‖≤ ¯ω1and‖˙ωdi(t)‖≤ ¯ω2for all t≥0.

Denote the error quaternion(ηi,η0,i)∈R3×R as the i th rigid body orientation of the body-fixed frame with respect to frame D.These error quaternions are subjectto the constraint=1 and are related to(ξi,ξ0,i)and(qi,q0,i)by the quaternion multiplication rule[10].The corresponding rotation matrix Ri=Ri(ηi,η0,i)∈S O(3)is given by Ri=(η20,i−the angular velocity errorω˜iof the i th rigid body can be written as

From(1)～(4),we can obtain the attitude-tracking error dynamics as follows

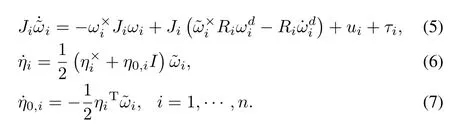
It can be seen from the above error system(5)and(6)that the rigid body attitude tracking problem is equivalent to the problem of asymptotic stabilization of˜ωiandηi.

B.Algebraic Graph Theory

In this paper,a general directed communication topology is adopted to describe the interaction between neighboring rigid bodies.Suppose G(V,E,A)is a directed graph,which consists ofa nonempty finite setof N nodes V={υ1,···,υn},a setof edges or arcs E⊂V×V and an associated weighted adjacency matrix A=[aij]∈RN×N.In our research,an arc(υi,υj) denotes that rigid bodyυican obtain the information of rigid bodyυj.It is assumed that the graph has no self-loops,i.e., (υi,υj)∈E impliesυi/=υj.The adjacency matrix A of G is a square matrix of size n with entries

where the nonnegative ai,jwill be chosen to be the control weightparameter for attitude synchronization between the i th and j th rigid bodies subsequently.In addition,we can note that ai,i=0 from(8).

Define the in-degree matrix D of G,which is a diagonal matrix with diagonal entries

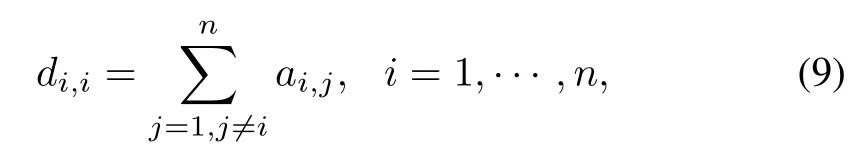
and the Laplacian matrix L∈Rn×nof graph G[20]

Remark 1.Note that a graph with the property that for any(υi,υj)∈ E,the edge or arc(υj,υi)∈ E is said to be undirected,which corresponds to having bidirectional measurementin the application ofrigid body attitude synchronization.Since the assumption ai,j=aj,iis valid in the undirected communication topology,the graph Laplacian matrix L becomes a symmetrical matrix,which makes the stability analysis of cooperative control system easier.However,in the directed communication topology,the graph Laplacian matrix L is generally not symmetric because ai,j/=aj,i.

C.Lemmas

Lemma 1[20].For a directed graph G with N nodes,all the eigenvalues of the weighted Laplacian matrix L have a nonnegative real part.

Lemma 2[21].If U∈Rm×m,V∈Rn×n,X∈Rm×m, and Y∈Rn×n,then the following arguments are valid:

2)If U and V are invertible,then(UV)−1=U−1V−1.

3)Letλ1,···,λmbe the eigenvalues of U andµ1,···,µmbe those of V.Then the eigenvalues of UV areλiµj(i= 1,···,m and j=1,···,n).

Lemma 3[22].If n＞0,m＞0,and a∈R,b∈R,then for any constant c＞0,

Definition 1[24].Consider the nonlinear system ˙x=f(x, u),where x is a state vector,and u is the input vector.The solution is practically finite-time stable(PFS)if for all x(t0) =x0,there existε＞0 and T(ε,x0)＜∞,such that‖x(t)‖＜ε,for all t≥t0+T.

Lemma 5[24].Consider the nonlinear system ˙x=f(x,u) defined above.If there exist continuous function V(x),scalar λ＞0,α∈(0,1)and 0＜η＜∞such that

then the trajectory of system ˙x=f(x,u)is PFS.

D.Control Objective

In this paper,in the presence of inertia uncertainties and environmental disturbances,we aim at tracking and attitude stabilization in rigid body formation with bounded energy.The tracking error of the i th rigid body is defined by

where k is a positive constant.The formation-keeping attitude state error between the i th and j th rigid bodies is defined by

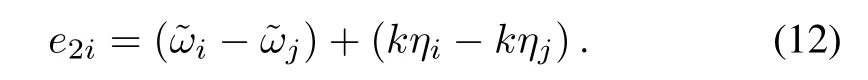
The multiple rigid bodies sliding mode vector is developed and defined as

where si∈R3×1,and it is given by

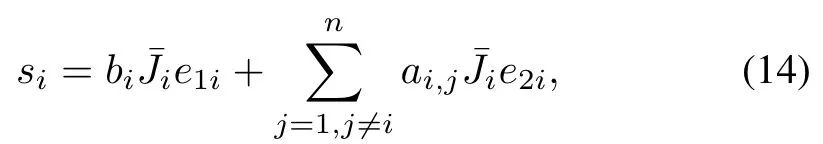
where¯Jiis the nominal inertia matrix of the i th rigid body, scalar bi＞ 0 is the control weight parameter for attitude tracking which is used to keep the i th rigid body station behavior,scalar ai,j≥0 is the control weight parameter for attitude synchronization between the i th and j th rigid bodies which is used to keep the formation behavior.

Using the Kronecker product,the multiple rigid bodies sliding mode vector(13)can be rewritten as

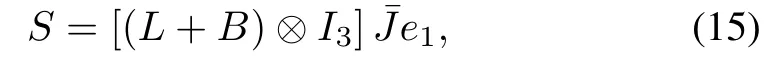
where L is the weighted Laplacian matrix which is described in(10),B=diag{b1,···,bn},¯J=diag{¯J1,···,¯Jn},and e1={e11,···,e1n}.

From Lemma 1,the third result in Lemma 2,and the definition of B,it follows that(L+B)I3has full rank. In addition,¯J has fullrank.Consequently,we obtain that[(L +B)I3]¯J has full rank.Thus,if the sliding-mode surface S=0 is reached,then e1=0,i.e.,e1i=0(i=1,···,n) will be satisfied,and we can get that

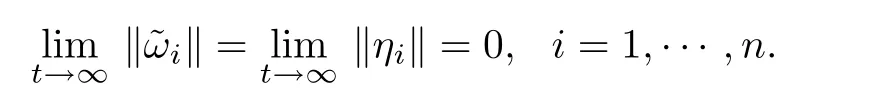
The controlobjective in this paper is to design a decentralized adaptive sliding mode control law such that the slidingmode surface defined in(13)can achieve PFS.

III.CONTROL LAW DESIGN

In this section,under a general directed communication topology,in the presence of the inertia uncertainties and environmental disturbances,a decentralized sliding mode control law is developed to ensure that the rigid body attitude error dynamics can converge to a neighborhood ofthe sliding-mode surface in a finite time.

Using(5)and(6),(16)～(18)are derived to develop the control law.

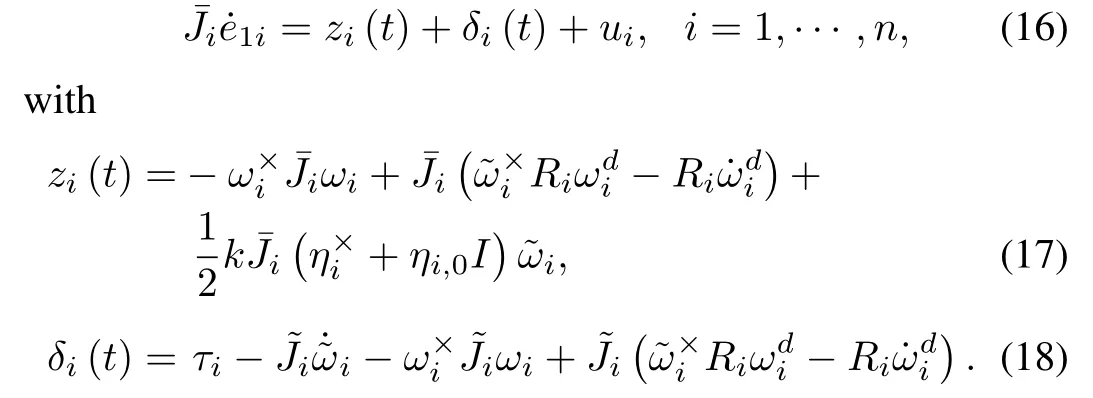
Following Assumptions 1～4 and the definitions of L and B, we assume that

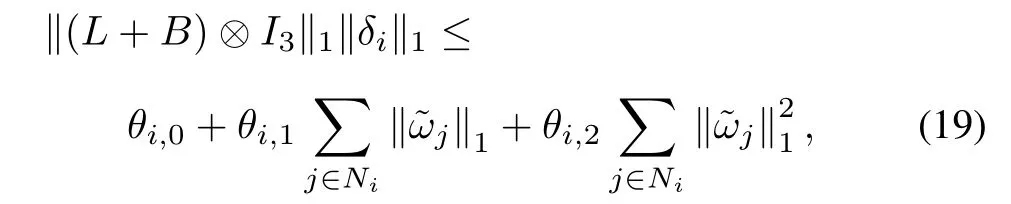
whereθi,0,θi,1,andθi,2are nonnegative constant numbers. Letˆθi,0,ˆθi,1,andˆθi,2denote the estimates ofθi,0,θi,1,and θi,2,respectively.Define the adaptive upper bound of the norm‖(L+B)⊗I3‖1‖δi‖1as

with i=1,···,n.Then the parameter adaptation errors can be written as˜θi,0= ˆθi,0−θi,0,˜θi,1= ˆθi,1−θi,1,and˜θi,2= ˆθi,2−θi,2.

According to the above discussions,the following theorem is given for the multiple rigid body attitude synchronization and tracking problems under the general directed communication topology.

据了解，鲁西集团自2010年至今共举办了九届员工职业技能大赛，随着企业不断地壮大，涉及的产业越来越多，大赛项目和参加人员、层次连年递增。竞赛项目由第一届的5个增加到17个，竞赛范围由单纯的生产岗位技能竞赛增加为涵盖办公自动、安全消防、安全驾驶、会计电算化等覆盖生产操作、后勤岗位的综合型大赛。随着集团员工实训基地的建设投用，赛项的承办由原来与技术院校共办，变为全部利用集团内资源开展竞赛活动。竞赛组织水平通过不断地总结提升，并借鉴省赛、国赛标准，逐步达到省级赛事水准。

Theorem 1.Consider the rigid body formation attitude tracking dynamics described by(5)～(7).Suppose that the decentralized adaptive sliding mode control law is designed as

and the adaptation laws are chosen as

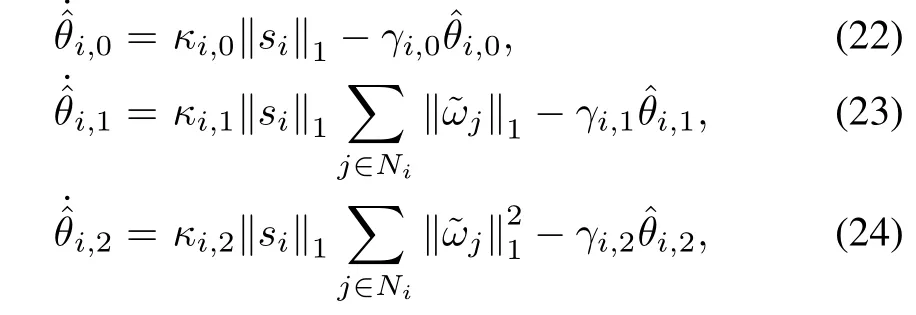
whereσ1,σ2,κi,j,γi,j,i=1,···,n,j=0,1,2,are positive constants and

If the Assumptions 1～4 are valid,then the sliding-mode surface defined in(13)can achieve PFS.

Proof.Define the candidate Lyapunov function as follows

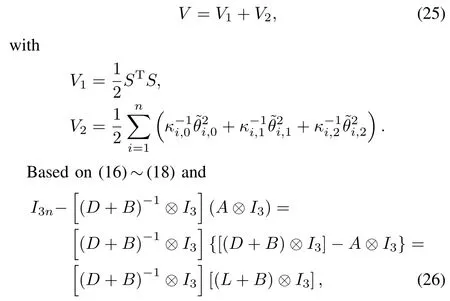
the adaptive sliding mode control law(21)can be rewritten as

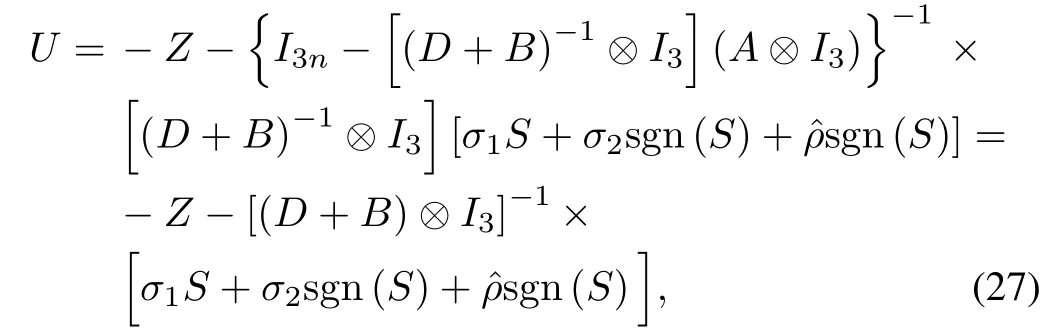
whereˆρ=diag{ˆρ1,···,ˆρn}.

From(15)and(16),it follows that the derivative of V1is

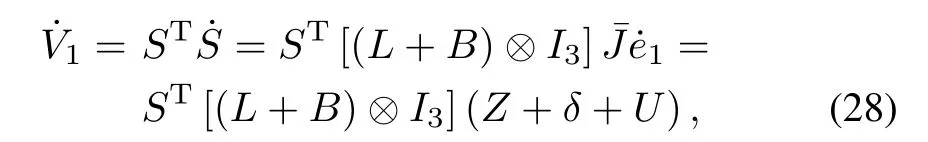
Introducing(27)to(28)and using(19)and(20)leads to

Using the adaptation laws in(22)～(24),it obtains the derivative of V2as follows

Based on(29)and(30),we getthe derivative of V as follows

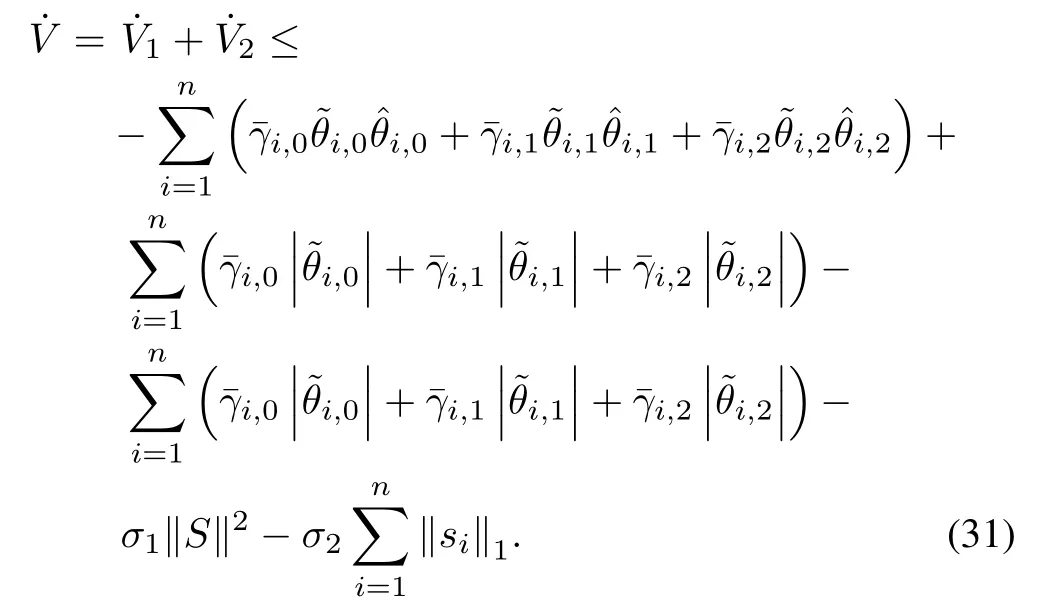
From Lemma 3,we obtain

Substituting inequalities(32)to(31),we have

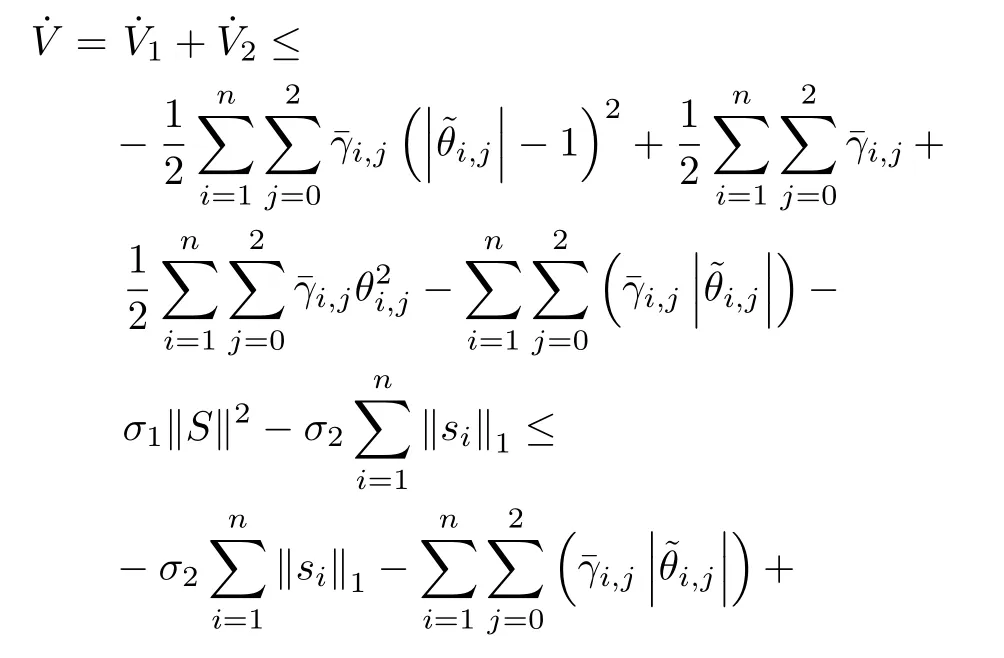
IV.MODIFIED CONTROL DESIGN

As the sign function is a piecewise continuous function,the proposed control laws,which are designed in(21),and adaptive laws in(22)～(24)are discontinuous across the surface, thus it will lead to control chattering.So we have to remedy this situation by smoothing out the control discontinuity in a thin boundary layer neighboring the switching surface by replacing the sign function by a saturation function in the control laws[25].The saturation function is defined as

According to the discussion above,the following theorem is given for the multiple rigid body attitude synchronization and tracking problem.

Theorem 2.Consider the rigid body formation attitudetracking dynamics described by(5)～(7).Suppose that the decentralized adaptive sliding mode control law is designed as(36),and the adaptation laws are chosen as(38)～(40).If Assumptions 1～4 are valid,then S'can achieve PFS.

Proof.Redefine the candidate Lyapunov function as

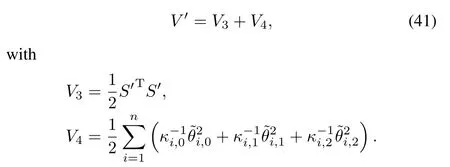
Rewrite the adaptive sliding mode control law(36)as

The derivative of V3can be obtained as Introducing(42)in(43)leads to

Based on(32),(44),(45)and Lemma 4,we get the derivative of V'as follows

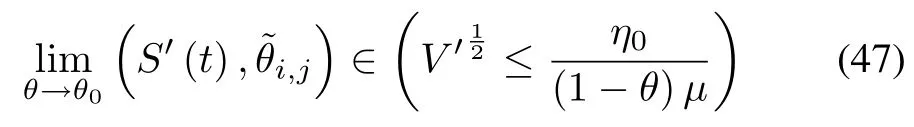
And the time needed to reach(47)is bounded asµθ0,where V'0is the initial value of V',0＜θ0＜1.

Remark 1.Though the boundary-layer leads to a small terminaltracking error,the practicaladvantages may be significant.Actually,for the practical implementations,due to the negative impact by external disturbances,sampled computation,etc.,the motion cannot reach the objective S=0 but moves along the sliding surface nearby[26−27].

Remark 2.In the proposed controllaws,the desired attitude of each rigid body with respect to the inertial frame is not restricted to be the same.Thus,the desired relative attitude among rigid bodies can be maintained.The communication topology has to satisfy some restrictions in many previous works(e.g.,undirected graph is connected,directed graph has a spanning tree,etc.),but there is no restriction on communication topology in our results.Thus,the proposed control laws can be applied to any communication topology, which means thatthe communication topology can be unconnected and does not have a spanning tree.The results are not restricted to be ring topology or undirected communication topology[19].Each rigid body is well controlled even when there has no communication link,which can be seen from the proof procedure and simulation section.

Remark 3.The need to maintain accurate relative orientation between rigid bodies is critical in many satellite formation missions,and there are more general requirements that need to be satisfied in practical applications,such as project Darwin(changed to next Gravitational-wave observatory(NGO)in 2011),in which four or five satellites fly in a tight formation to perform analysis of Earth-like planets,and micro SAR,consisting of small low-cost synthetic aperture radar(SAR)satellites capable of land and sea observations. The reference attitude trajectories are chosen such that the satellite motion is coordinated if all of the satellites are able to follow their reference trajectory accurately[28].This paper designs the control laws that are robust to the disturbances and uncertainties,and also can achieve high precision tracking and synchronization.The values of parameters designed in the sliding mode,control law and adaptation laws should be further tuned using extensive simulations.Further work includes extending the results in this paper to cases where there exist communication delays among rigid bodies and the angular velocity is not available.

V.NUMERICAL EXAMPLES AND SIMULATIONS

In this section,simulations for rigid bodies attitude synchronization and tracking are presented to illustrate the effectiveness of the proposed control approaches.

Example 1.To have a fair comparison of the dynamic performances of the proposed controller in this paper and the controller in[13],we consider two scenarios with four rigid bodies.In the firstscenario,a directed line topology,as shown in Fig.1(a),is considered for in-track(in-plane)formation.In the second scenario,a ring topology is considered for circularlike formation,as shown in Fig.1(b).Itis worth noting thatthe spanning trees of the communication graphs have no influence on the validity of the control law.

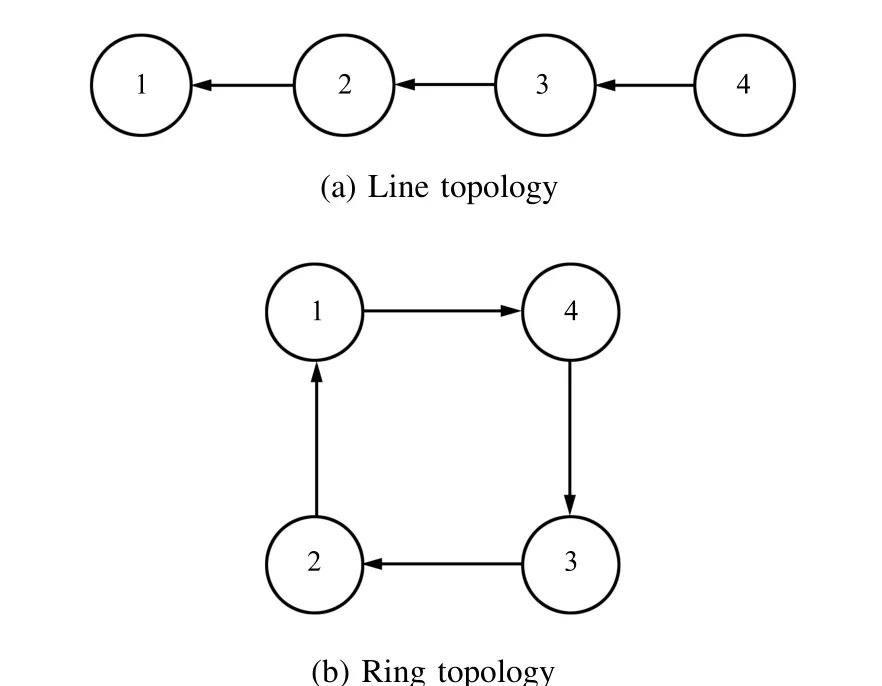
Fig.1.Directed communication topologies.

Give the corresponding weighted Laplacian matrices as

Consider the rigid body model(5)～(7)with the actual inertia matrices given by(with unit expressed in kg·m2)

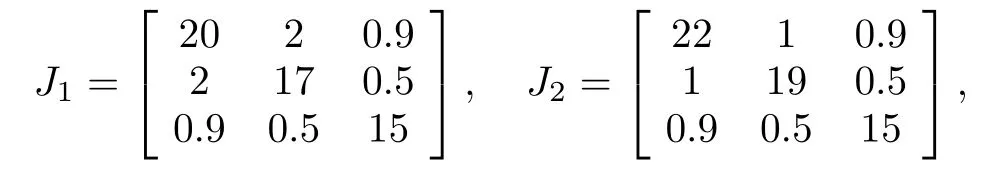
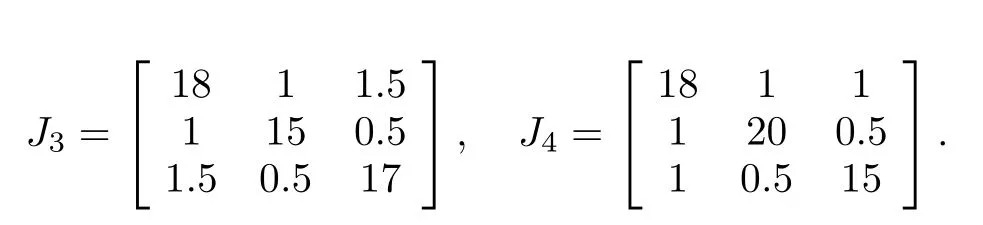
With the existence of model uncertainties and external disturbances,the nominal inertia matrices of the rigid bodies are given by

Choose the initialangular velocity errors of allrigid bodies to be zero,and the initial attitude-tracking errors given as follows

The initial desired quaternion is

Assume that the time-varying desired angular velocities of the rigid bodies are identical and given as

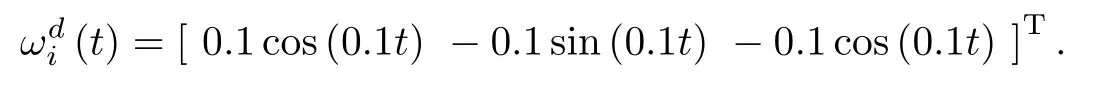
In the simulation,we assume that|ui,j|≤2 N·m,for i=1, 2,3,4,j=1,2,3.

A.Under the Line Communication Topology

In the first scenario,the controller parameters are selected as[19]σ1=0.01,σ2=9,k=1,bi=1,a1,2=1,a2,3=1, a3,4=1,a4,1=0,ϕ=0.15,and the parameters of the adaptation laws in(38)～(40)are chosen asκi,0=0.1,κi,1= κi,2=0.2,γi,0=γi,1=γi,2=1,for i=1,2,3,4,the initial values ofˆθi,0,ˆθi,1,ˆθi,2are given byˆθ0i,0= ˆθ0i,1= ˆθ0i,2=0.

Using the control law(36),Fig.2(a)shows the attitude tracking error of the second rigid body;for convenience of interpretation,attitude errors are expressed in Euler angles converted from unit quaternion.Attitude tracking errors of other rigid bodies are similar to those of the second rigid body. Fig.3(a)shows the relative attitude error between the firstand fourth rigid bodies.Relative attitude errors between otherpairs of rigid bodies are similar to Fig.3(a).The controltorque(36) ofthe second rigid body is shown in Fig.4(a).The response of the adaptive parametersˆθ2,0,ˆθ2,1,ˆθ2,2as defined in(17),are shown in Fig.5(a),and thus the efficacy ofthe adaptation laws (38)～(40)is verified.The response of the sliding mode s'2is given in Fig.6(a).The control torques,adaptive parameters and sliding modes of other rigid bodies are similar to those of the second rigid body,and are not plotted here due to space constraint.The corresponding performance indexes using the controller in[13]are shown in Figs.2(b)～6(b).

As observed from the simulation fi gures,Figs.2～6,we can see that the response of attitude tracking error and relative attitude error between rigid bodies,as shown in Figs.2(a)and 3(a),have slightly faster convergence rate and higher accuracy than those using the controller in[13].

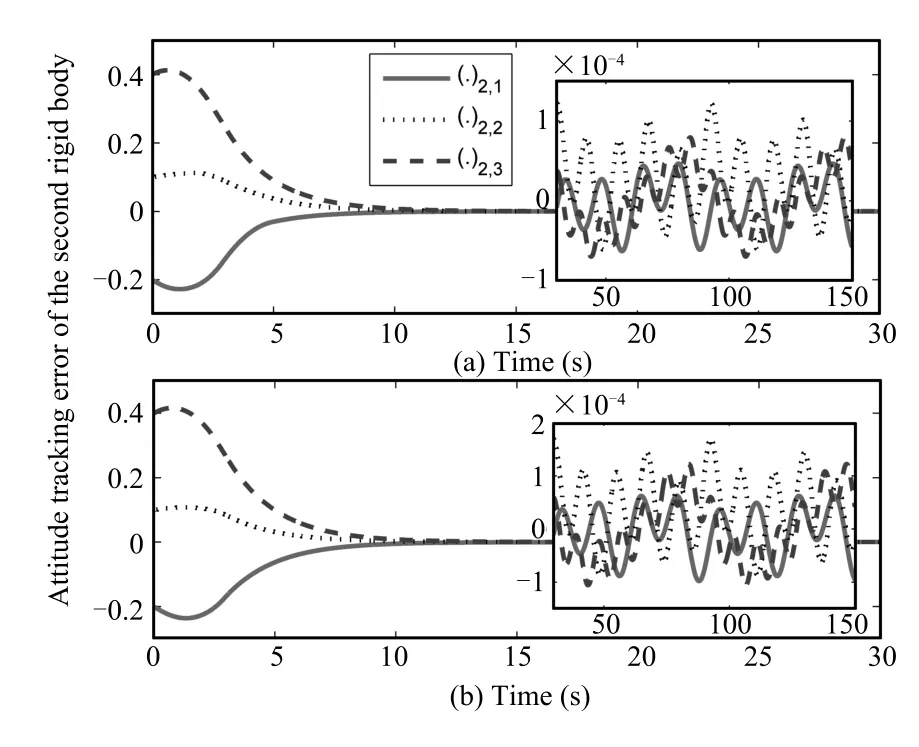
Fig.2. Attitude tracking error of the second rigid body.

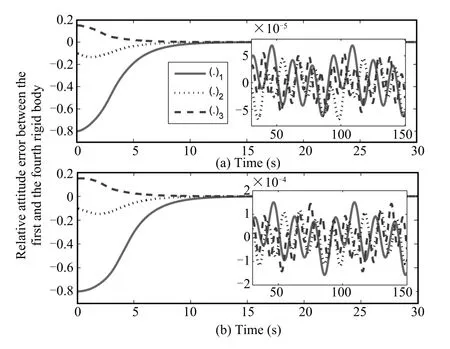
Fig.3.Relative attitude error between the first and the fourth rigid bodies under the line topology.

Fig.4. Control torque of the second rigid body.

B.Under the Ring Communication Topology

Under the ring communication topology,we choose all the controller parameters as the first subsection,except that a4,1=1 in this subsection.Figs.7(a)and 8(a)show the attitude tracking error of the second rigid body and relative attitude error between the first and fourth rigid bodies using the control law(36),respectively.Figs.7(b)and 8(b)arethe corresponding performance indexes using the controller in[13].As observed from Figs.2(a),3(a),7(a)and 8(a),we can see that the attitude tracking error and relative attitude error in the ring topology are slightly smaller than those in the line topology,because of the additional coupling between the fourth and first rigid bodies in the ring topology.Furthermore,similar to Subsection 4.1,we can conclude that the responses ofattitude tracking errors and relative attitude errors between rigid bodies using controller(36)show slightly faster convergence rate and higher accuracy than those using the controllerin[13],as shown in Figs.7 and 8,and we omitother comparing figures due to space constraint.Thus,the simulation results validate the effectiveness of the proposed control law under a unidirectional ring communication topology.

Fig.5. Adaptive parametersˆθ2,0,ˆθ2,1,ˆθ2,2ofthe second rigid body.

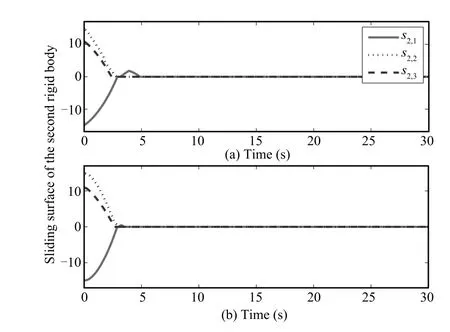
Fig.6. Sliding surface of the second rigid body.

VI.CONCLUSIONS

In this paper,based on the sliding mode controland adaptive control techniques,in the presence of inertia uncertainties and environmental disturbances,two novel decentralized adaptive sliding mode control laws are proposed to ensure that the sliding modes S and S'can achieve PFS,respectively.Detailed simulation results have been presented to illustrate the developed method.Further work includes extending the results in this paper to cases where there exist communication delays between rigid bodies and the angular velocity is notavailable.

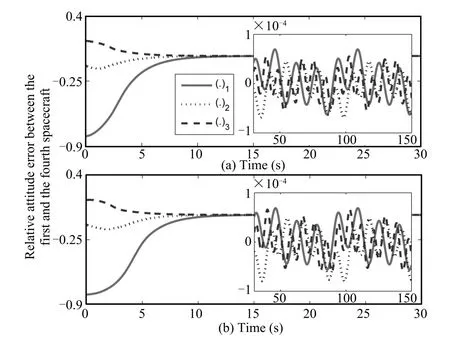
Fig.8. Relative attitude error between the first and the fourth rigid bodies under the ring topology.

REFERENCES

[1]Du H B,Li S H,Qian C J.Finite-time attitude tracking controlof spacecraft with application to attitude synchronization.IEEE Transactionson Automatic Control,2011,56(11):2711−2717

[2]Igarashi Y,Hatanaka T,Fujita M,Spong M W.Passivity-based attitude synchronization in SE(3).IEEE Transactions on Control Systems Technology,2009,17(5):1119−1134

[3]Dong X G,Cao X B,Zhang J X,Shi L.A robust adaptive control law for satellite formation flying.Acta Automatica Sinica,2013,39(2):128−137

[4]Peng J M,Wang J N,Ye X D.Distributed adaptive tracking control for unknown nonlinear networked systems.Acta Automatica Sinica,2013, 39(10):1729−1735

[5]Cao Y C,Ren W.Distributed coordinated tracking with reduced interaction via a variable structure approach.IEEE Transactionson Automatic Control,2012,57(1):33−48

[6]Suul J A,Luna A,Rodriguez P,Undeland T.Voltage-sensor-less synchronization to unbalanced grids by frequency-adaptive virtual flux estimation.IEEE Transactions on Industrial Electronics,2012,59(7): 2910−2923

[7]Lawton J R,Beard R W.Synchronized multiple spacecraft rotations. Automatica,2002,38(8):1359−1364

[8]Abdessameud A,Tayebi A.Attitude synchronization of a group of spacecraft without velocity measurements.IEEE Transactions on AutomaticControl,2009,54(11):2642−2648

[9]Bai H,Arcak M,Wen J T.Rigid body attitude coordination without inertial frame information.Automatica,2008,44(12):3170−3175

[10]Ren W.Distributed cooperative attitude synchronization and tracking for multiple rigid bodies.IEEE Transactions on Control Systems Technology,2010,18(2):383−392

[11]Min Hai-Bo,Liu Zhi-Guo,Liu Yuan,Wang Shi-Cheng,Yang Yan-Li. Coordination control of networked Euler-Lagrange systems with possible switching topology.Acta Automatica Sinica,2013,39(7):1003−1010(in Chinese)

[12]Zhou N,Xia Y Q,Lu K F,Li Y.Decentralised finite-time attitude synchronisation and tracking control for rigid spacecraft.International Journal of Systems Science,2013,doi:10.1080/00207721.2013.868949

[13]Zhou N,Xia Y,Wang M,Fu M.Finite-time attitude controlof multiple rigid spacecraft using terminal sliding mode.International Journal of Robustand Nonlinear Control,2014,doi:10.1002/rnc.3182

[14]Khoo S Y,Xie L H,Man Z H.Robust finite-time consensus tracking algorithm for multirobot systems.IEEE/ASME Transactionson Mechatronics,2009,14(2):219−228

[15]Chen Y P,Lo S C.Sliding-mode controllerdesign forspacecraftattitude tracking maneuvers.IEEE Transactions on Aerospace and Electronic Systems,1993,29(4):1328−1333

[16]Lo S C,Chen Y P.Smooth sliding-mode control for spacecraft attitude tracking maneuvers.Journal of Guidance Control and Dynamics,1995, 18(6):1345−1349

[17]Chen Z Y,Huang J.Attitude tracking and disturbance rejection of rigid spacecraftby adaptive control.IEEETransactionsonAutomatic Control, 2009,54(2):600−605

[18]Ahmed J,Coppola V T,Bernstein D S.Adaptive asymptotic tracking of spacecraft attitude motion with inertia matrix identification.Journal of Guidance,Control,and Dynamics,1998,21(5):684−691

[19]Wu B L,Wang D W,Poh E K.Decentralized robustadaptive controlfor attitude synchronization underdirected communication topology.Journal of Guidance,Control,and Dynamics,2011,34(4):1276−1282

[20]Merris R.Laplacian matrices of graphs:a survey.Linear Algebra and Its Applications,1994,197−198(5):143−176

[21]Horn R A,Johnson C R.TopicsinMatrixAnalysis.Cambridge,England, UK:Cambridge University Press,1991.242−254

[22]Qian C J,Lin W.A continuous feedback approach to global strong stabilization of nonlinear systems.IEEE Transactions on Automatic Control,2001,46(7):1061−1079

[23]Hardy G H,Littlewood J E,Polya G.Inequalities.Cambridge,England, UK:Cambridge University Press,1952.

[24]Zhu Z,Xia Y Q,Fu M Y.Attitude stabilization of rigid spacecraft with finite-time convergence.International Journal of Robust and Nonlinear Control,2010,21(6):686−702

[25]Slotine J J E,Coetsee J A.Adaptive sliding controller synthesis for nonlinearsystems.InternationalJournalofControl,1986,43(6):1631−1651

[26]Lu K F,Xia Y Q.Adaptive attitude tracking control for rigid spacecraft with finite-time convergence.Automatica,2013,49(12):3591−3599

[27]Shtessel Y,Taleb M,Plestan F.A novel adaptive-gain supertwisting sliding mode controller:Methodology and application.Automatica, 2012,48(5):759−769

[28]Zhou J K,Hu Q L,Friswell M I.Decentralized finite time attitude synchronization controlofsatellite formation flying.JournalofGuidance Control and Dynamics,2013,36(1):185−195

Yuanqing Xia Professor at the School of Automation,Beijing Institute of Technology.His research interests include networked control systems,robust control,active disturbance rejection control and flight control.Corresponding author of this paper.

Ning Zhou Ph.D.candidate at the School of Automation,Beijing Institute of Technology.Her research interests include attitude synchronization, finite-time control,sliding mode control,and fuzzy control.

Kunfeng Lu Ph.D.candidate at the School of Automation,Beijing Institute of Technology.His research interests include spacecraftattitude control, finite-time control,sliding mode control,and adaptive control.

Yong Li Professor and principle investigator of Qian Xuesen Laboratory of Space Technology,China Academy of Space Technology.His main research interest is spacecraft control.

t

July 3,2013;accepted April 15,2014.This work was supported by National Basic Research Program of China(973 Program) (2012CB720002),National High Technology Research and Development Program of China(863 Program)(2012AA120601),National Natural Science Foundation of China(61225015),the Ph.D.Programs Foundation of Ministry of Education of China(20111101110012),and China Academy of Space Technology(CAST)Foundation(CAST201210).Recommended by Associate Editor Changyin Sun

:Yuanqing Xia,Ning Zhou,Kunfeng Lu,Yong Li.Attitude control of multiple rigid bodies with uncertainties and disturbances.IEEE/CAA Journal of Automatica Sinica,2015,2(1):2−10

Yuanqing Xia,Ning Zhou,and Kunfeng Lu are with the Schoolof Automation,Key Laboratory of Intelligent Controland Decision of Complex Systems, Beijing Institute of Technology,Beijing 100081,China(e-mail:xiayuanqing@bit.edu.cn;zhouning2010@gmail.com;kunfenglu001@gmail.com).

Yong Li is with the Qian Xuesen Laboratory of Space Technology, China Academy of Space Technology,Beijing 100094,China(e-mail:liyong@cast.cn).