栓接结合部迟滞非线性等效线性化方法
李 玲,蔡安江,阮晓光,王战胜
(1.西安建筑科技大学机电工程学院,陕西西安710055;2.洛阳电光设备研究所,河南洛阳471009)
栓接结合部迟滞非线性等效线性化方法
李 玲1,蔡安江1,阮晓光1,王战胜2
(1.西安建筑科技大学机电工程学院,陕西西安710055;2.洛阳电光设备研究所,河南洛阳471009)
由于栓接结合部强的非线性特性,要建立和求解这类非线性模型以及实现与其他模型的耦合极为困难。为体现栓接结合部等效非线性特性和便于工程应用,首先将结合面简化为光滑刚性平面与粗糙表面的接触问题,建立单个微凸体力-位移本构关系;然后根据 Masing准则和切向力模型,建立栓接结合部在单个循环周期下的恢复力模型,并假设在稳态激励和振动幅值很小的情况下,利用平均法建立栓接结合部等效线性化的刚度与阻尼模型。为验证所建栓接结合部恢复力模型和等效线性化模型的正确性,分别搭建恢复力实验平台和模态测试实验平台,并利用有限元法将栓接结合部等效线性化模型与有限元模型耦合,建立考虑栓接结合部特性的整体结构动力学模型,最终通过两组实验验证两类模型的正确性。
栓接结合部;迟滞非线性特性;恢复力模型;等效线性化模型
引 言
在振动环境中,由于机械系统受到外界力、边界条件和结合面等因素的影响,使得栓接结合部具有强的非线性特性[1]。其主要特征为:在切向可能发生相对滑移;在法向可能发生间隙分离和冲击碰撞。滑移形式既包括只发生在结合部局部区域上的微观尺度上的滑移,又有结合部整体相对运动的宏观尺度上的滑动;间隙和碰撞形式也既包括微观尺度上的拍击,还有宏观尺度上的分离碰撞[2]。
为研究这种复杂的非线性行为,2000年美国Sandia国家实验室在征求知名工程研究人员、学者和项目管理者的建议下发布白皮书[3],提出采用标准试件开展栓接结合部动力学行为建模和预测方法的研究。之后分别于2006年、2009年和2012年,该研究团队三次召开国际栓接结合部工作总结和未来研究规划大会。在会上针对栓接结合部多尺度下的研究路径图[4],各研究小组提出了各自的研究方案和思路,为进一步研究栓接结合部非线性特性开拓了道路。其中,Ahmadian提出建立一种通用连接单元来表示栓接结合部的非线性[5],并将这种单元引入到结构控制方程中。Segalman[6]发展了一种含有4个参数的Iwan模型以描述栓接结合部的动态特性。Song等[2]提出一种改进的Iwan模型用于模拟栓接结合部随外载荷非线性变化的粘滑行为。Xue[7]在Bouc-Wen模型的基础上开发了一种非线性连接部件单元。Oldfield[8]把Iwan模型和Bouc-Wen模型与有限元单元法相结合,对栓接结合部在周期载荷作用下的响应进行了计算。Miller和Quinn[9]提出了一个双边的接触面摩擦能量损耗模型,该模型用两个Jenkins单元链来表示两个接触界面。Jalali等[10]利用力状态映射法将栓接结合部的非线性方程转化在模态坐标下求解,解决了试验时难以获得结合面处的相对位移和力向量。在中国较早开展结合部特性研究的黄玉美团队,提出了一套系统研究栓接结合部特性参数的试验装置及影响因素的处理方法[11-12]。另外,作者近年针对栓接结合部的非线性特性也进行了相关研究[13-14]。
1 恢复力模型
为获得栓接结合部迟滞非线性特性,设计如图1(a)所示的连接件。其中,结构件(1)和结构件(2)是通过两块压板(3)与两个规格相同的螺栓连接在一起。连接件同时受到螺栓预紧力(法向力)和切向力F的作用,其迟滞非线性特性是通过一组线性弹簧和阻尼器进行等效,如图1(b)所示。

图1 栓接结合部和等效的线性模型Fig.1 The bolted joints and its mathematical idealization
图2 为栓接结合部的迟滞曲线。该曲线是在力拉伸试验机(MTS,INSTRON8801)中,通过设置波形、相位角、激励频率、激励幅值等参数后,进行力拉伸实验获得。图中Fd和Fl分别表示加载和卸载时的恢复力,xmax表示在外加载荷下的极限位移,位移x和恢复力F所围成的滞回曲线面积恰好是栓接结合部位移变化一周时恢复力所耗能量[15]。

图2 加载和卸载过程栓接结合部迟滞曲线Fig.2 The hysteresis curves of bolted joints
1.1 单个微凸体受力分析
由于栓接结合部这种迟滞非线性特性来源于微观接触表面上无数个微凸体间的相互影响、相互制约和相互依赖[16]。为便于研究,将结合面简化为光滑刚性平面与粗糙表面的接触问题[17-18],如图3所示。图中R表示微凸体的半径;λn表示结合面的法向位移量,λn=αPmn,Pn为平均表面压,α和m是由结合面加工方法和材料等决定的常数[19];z表示两接触表面间的平均距离;y表示法向变形量,y=λn-z。
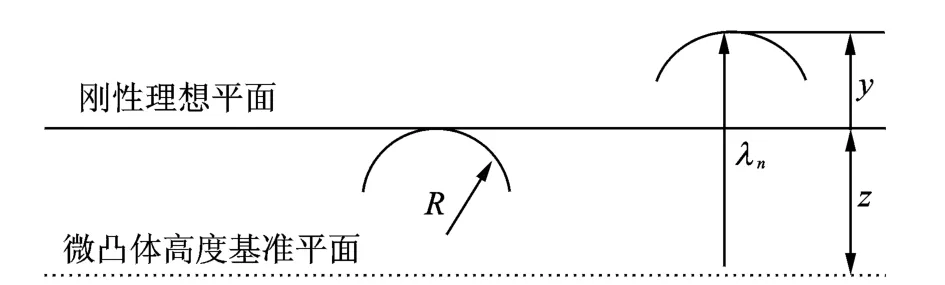
图3 结合面的接触变形示意图Fig.3 The schematic diagram of two contact surfaces with deformation
当微凸体的变形未超出弹性范围时,根据Hertz接触理论,可得单个微凸体的法向接触载荷为

式中 E*为两接触材料的复合弹性模量。

其中 E1,E2为两接触材料的弹性模量;υ1,υ2为两接触材料的泊松比。
而根据文献[20],可得单个微凸体的切向接触载荷为
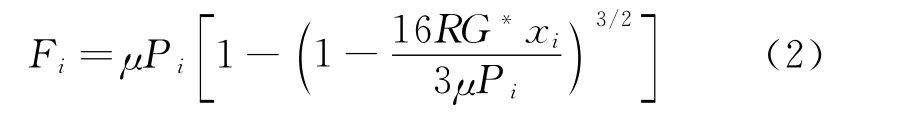
式中 μ为摩擦系数;x为切向位移;G*为两接触材料的复合剪切模量。
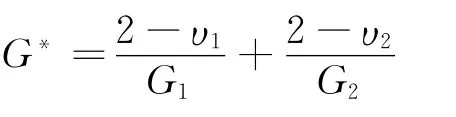
其中 G1,G2为两材料的剪切模量。
实际上,式(1)和(2)分别表示在弹性范围内,单个微凸体所受法向力、切向力与相应位移变形的关系表达式。
1.2 恢复力模型
根据式(2)单个微凸体的切向力-位移关系可知,当切向变形量

则单个微凸体在弹性范围内最大受力为Fi=μPi。所以在弹性范围内两接触表面间的最大距离为
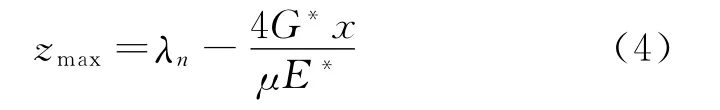
根据文献[21]可得,栓接结合部的切向力F可表示为。
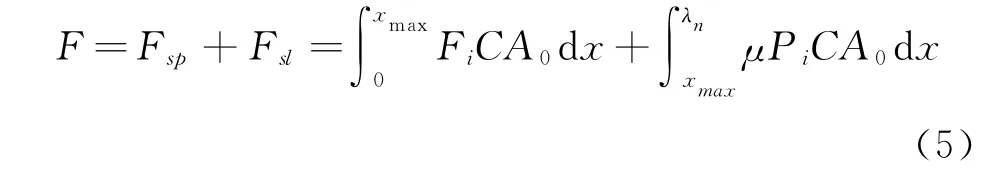
式中 Fsp为微凸体没有超过最大切向变形极限的切向力;Fsl为微凸体已超出最大切向变形极限的切向力;C为表面参数,与单位面积微凸体的接触数量有关,取C=1×1010[21];A0为真实接触面积。
根据式(2)和(5),可得切向力Fsp与Fsl的表达式分别为

将式(6)和(7)代入式(5)中,可得栓接结合部的切向力为
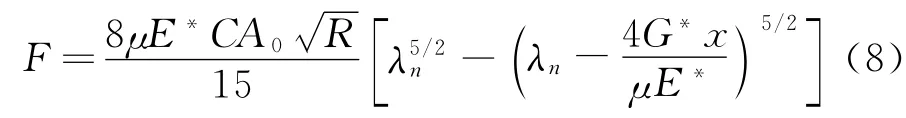
将式(8)简化为

式中 Δ为最大切向变形量。
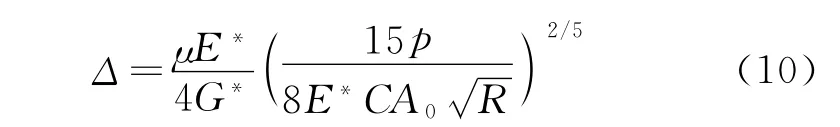
其中 p为螺栓传递扭矩的法向力。

根据Masing准则[22],整个过程的力-位移变形关系如图2所示,卸载过程中的恢复力曲线可以通过(x0,F0)表示为
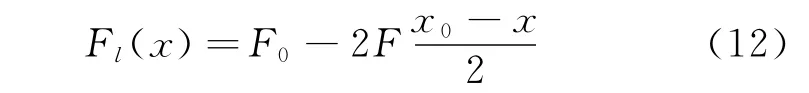
式中 F0为迟滞曲线中位移x0处所受到的力。
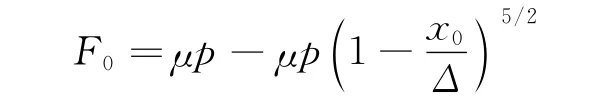
联合式(9)和(12)可得卸载过程恢复力为

Masing准则表明,在加载和卸载过程中,恢复力函数F(x)满足如下关系

式中 Fd(x)为加载时的恢复力函数。
所以,式(13)和(14)即为栓接结合部加载和卸载过程的恢复力模型。若已知微凸体的真实接触面积A0、半径R以及结合面的法向位移量λn,即可获得栓接结合部的迟滞曲线。
2 线性化方法
为便于工程分析,假设整个过程为稳态激励,即x=b cosθ=b cosωt,在很小的幅值b和频率ω下发生切向变形,根据平均法,利用等效线性化刚度和阻尼替代栓接结合部在一个周期中的迟滞非线性关系,即F*(x)=keqx+deqx'。等效刚度keq与等效阻尼deq可通过式(15)和(16)获得

根据式(14)~(16)之间的关系,可得

将式(13)代入式(17)可得等效线性化刚度
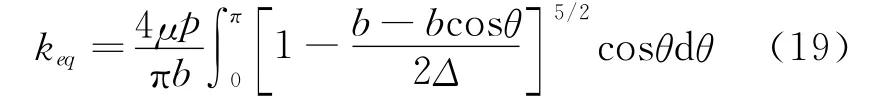
当振动幅值很小(b/Δ≪1)时,式(19)可近似表示为
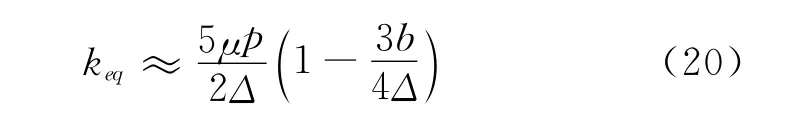
将式(13)代入式(18)可得等效线性化阻尼
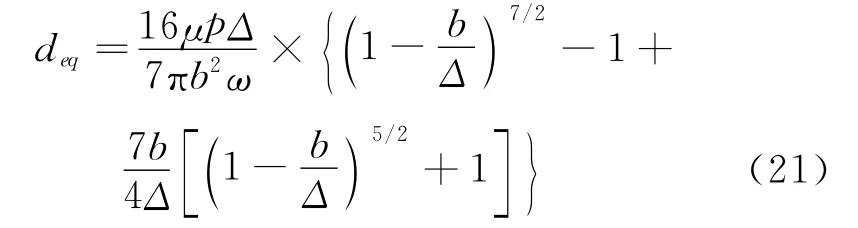
同理,当振动幅值很小时,式(21)可近似表示为

式(21)和(22)即为栓接结合部等效线性化刚度和线性化阻尼模型。利用该模型可以将栓接结合部的等效线性化参数与各子结构模型耦合,从而获得整体结构的动态特性。
3 算 例
3.1 搭建恢复力实验平台
本实验台主要由INSTRON8801力学拉伸实验机、动态应变仪BZ2688、LMS模态测试系统、高强度螺栓M16、计算机以及试件(1)与试件(3)等组成。试件(1)与试件(2)结构尺寸相同,间隙为2 mm,试件材料均为Q235,结合面处经过磨削处理。高强度螺栓沿轴向植有应变片,其输出端连一电桥,通过动态应变仪BZ2688接入LMS信号采集系统,调节螺栓预紧力的大小,可以获得结合面所受的面压。INSTRON8801力学拉伸实验机用于拉压连接件时,获取栓接结合部在不同预紧力下的力与位移实验数据。实验原理如图4所示。

图4 实验原理Fig.4 Experimental principle
采用位移控制模式,设置波形为正弦波,波形初始相位为0,相位角增量为0,频率为0.02 Hz。设置螺栓预紧力为20 k N,振幅分别为A1=30μN,A2=50μN,A3=80μN,A4=100μN,稳态激励方式如图5所示。在一个循环周期下获得栓接结合部滞迟曲线如图6所示。
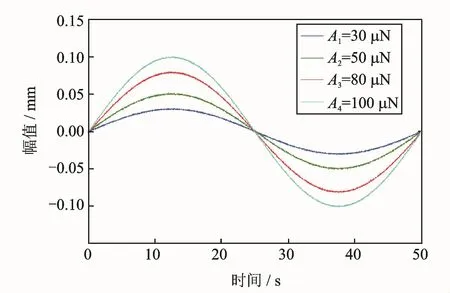
图5 正弦波激励Fig.5 Exciting mode of sinusoidal wave
由图6可知,在预紧力为20 k N时,迟滞环的面积随着稳态激励幅值A的增加而增加,且迟滞环趋于双线性模型。基于上述实验条件,获得不同预紧力下的试验结果与上述结论类似。故针对栓接结合部的非线性特性,在振动幅值很小时,可以采用线性化的方法将其等效为线性弹簧和阻尼器。从解决实际工程问题出发,将非线性问题线性化后不仅便于工程应用,同时也提高了模型的运算速度。

图6 不同激振幅值下的力-位移迟滞曲线Fig.6 The force-displacement hysteresis cycles in different vibration amplitudes were tested
根据栓接结合部恢复力实验结果,以A1=30μN和A3=80μN为例,运用所建立的恢复力模型,对栓接结合部在一个循环周期中的力-位移变形过程进行数值仿真,并与实验结果比较,结果如图7所示。图中实验与仿真2条曲线基本重合,从而表明所建恢复力模型的正确性,和利用该模型能够模拟在振动幅值很小时的栓接结合部迟滞非线性特性。

图7 实验与仿真结果比较Fig.7 The force-displacement hysteresis cycles were tested and simulated
3.2 等效刚度与等效阻尼的计算
由于试件材料均为Q235,所以取弹性模量E=173 GPa,剪切模量G=44.3 GPa,泊松比υ=0.3,根据复合弹性模量和复合剪切模量公式可得E*和G*;根据文献[19]附表中的参数,结合面磨削后取α=0.65,m=0.5,所以由λn=αPmn可求取结合面的法向位移变形量λn;根据文献[21]取C=1×1010,R=100μm,由式(11)可求得结合面的真实接触面积A0。
当上述参数均已获取后,根据式(20)和(22)可分别求得栓接结合部等效线性刚度和阻尼值为7.3×107N/m和21.8 N·s/m。则该等效数值可通过有限元软件将其与试件(1)、试件(2)以及压板(3)的有限元模型耦合,最终求得整体结构的动力学特性,具体方法下小节所述。
3.3 栓接结合部特性与子结构模型的耦合
为将上述获得的等效线性刚度和阻尼特性与各试件的有限元模型耦合,建立考虑栓接结合部特性的整体结构有限元模型。首先忽略结构(1)、结构(2)和压板(3)的螺栓孔,将填充的实体部分等效为螺栓、螺帽和螺栓头的质量,利用Hypermesh软件对试件进行网格划分,并限制结合面处的节点。然后利用ANSYS的APDL语言自行编制程序,采用节点间路径最短的原则,将结合面上各节点进行连接,并利用Matrix27单元定义栓接结合部的等效刚度和等效阻尼参数,从而建立考虑栓接结合部的整体有限元模型,如图8所示。由于栓接结合部法向与切向等效刚度与阻尼之间的耦合特性对最终结果影响可以忽略不计[23],所以在对Matrix27单元进行定义时,将除主对角线以外的参数定义为0。

图8 整体有限元模型Fig.8 Finite model of whole structure
根据栓接结合部在不同预紧力下的等效参数值,利用图8所建立的整体结构有限元模型进行谐响应分析,最终获得不同预紧力下整体结构的频响函数,通过下小节的实验可验证所建模型的正确性。
3.4 实验验证
搭建整体结构模态测试实验平台,获取整体结构的频响函数,实验原理如图9所示。以锤击法作为激振方式,以加速度传感器在指定的位置上获取加速度信号作为输出信号。实验以先粗扫频后细扫频的方式进行,在搜索结构固有频率时采用粗扫频方式,大致确定结构固有频率的大小后,再通过细扫频方式确定固有频率的精确值,根据上述方法选取的频率范围为0~1 800 Hz,频率采样为2 Hz。
模态实验时所采用的激振点与拾取点如图10所示。在z方向上,点1和点2互为激振与拾取点,通过力锤的激振和加速度传感器的获取,可得原点频响函数H(1,1),H(2,2)和跨点频响函数H(1,2),H(2,1)。由于模型的对称性,可根据Maxwell互易性原理,通过跨点频响函数H(1,2)和H(2,1)验证试验方法的正确性。

图9 模态实验原理Fig.9 Experimental principle of modal characteristics
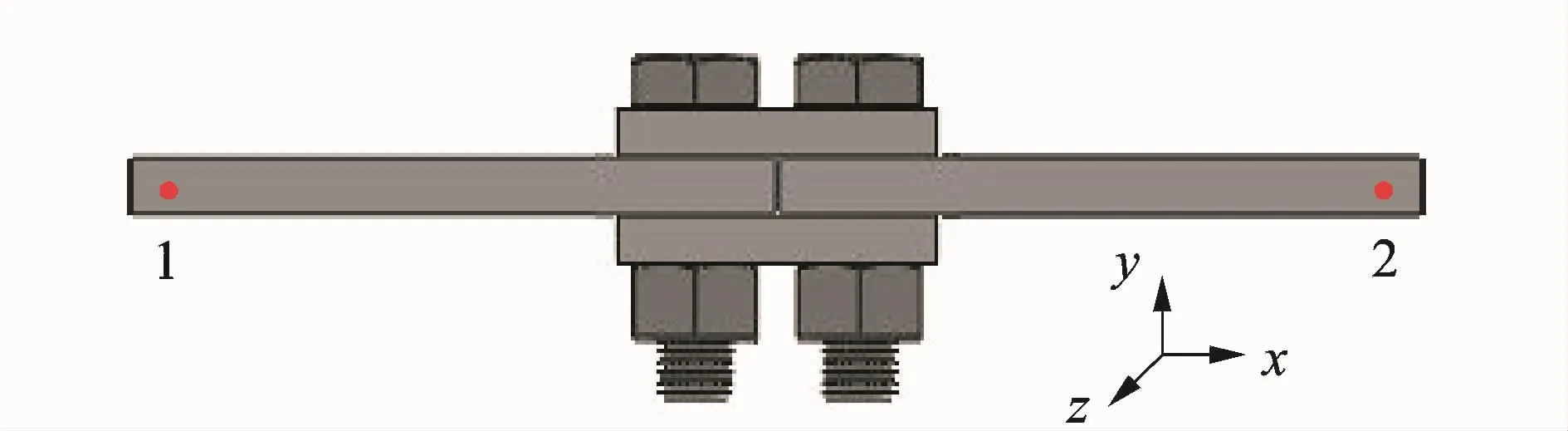
图10 模态实验时激振点的设置Fig.10 Modal test using electrodynamic shaker in three directions of z
根据3.3节所建立的考虑栓接结合部特性的整体结构有限元模型进行谐响应分析,和本节对整体结构的模态试验,比较两种不同方法获得的频响函数,验证所建立的线性化模型正确性。实验与仿真结果如图11和12所示。

图11 z方向上模态实验与有限元方法结果比较(频响函数(H(1,1))Fig.11 Compare experimental and paper's method for FRFH(1,1)of whole structure in directions of z

图12 z方向上模态实验与有限元方法结果比较(频响函数(H(1,2))Fig.12 Compare experimental and paper's method for FRFs H(1,2)of whole structure in directions of z
图11 和12是z方向上频响函数H(1,1)和H(1,2)的模态实验值与有限元仿真结果比较。两图表明,将栓接结合部等效线性化的刚度与阻尼值利用Matrix27单元嵌入整体结构中所获得的频响函数与模态实验所得的频响函数基本一致。通过模态实验获得的前两阶固有频率分别为598和1344 Hz;有限元仿真出来的结果为610.2和1 365 Hz,以模态实验数据为准确值,则前两阶误差分别为0.37%和1.56%,均未超过5%,从而表明,在小振幅下栓接结合部非线性特性完全可以进行线性化处理。
4 结 论
(1)将结合面的非线性问题转化为光滑刚性平面与粗糙表面的接触问题,建立单个微凸体力-位移本构关系,根据Masing准则和切向力模型,建立栓接结合部在一个循环周期下的加载和卸载恢复力模型,并通过搭建恢复力实验平台验证所建恢复力模型的正确性。
(2)假设结构在稳态激励和振动幅值较小的情况下工作,利用平均法建立栓接结合部等效线性化的刚度与阻尼模型,并利用有限元法将该线性化参数与各子结构有限元模型耦合,建立考虑栓接结合部特性的整体结构动力学模型,通过模态实验研究前两阶的固有频率,最大误差为1.56%,从而表明所用方法和所建模型的正确性。
(3)由于栓接结合部非线性动力学行为极其复杂,没有专门的分析工具,也没有通用性很强的有限元软件对整体结构的动态特性进行分析。将此类非线性问题线性化,并嵌入现有商业有限元软件中进行整体结构动力学特性分析,是解决工程问题的一种高效可行的研究方法。
[1]IBRAHIMR A,PETTIT C L.Uncertainties and dynamic problems of bolted joints and other fasteners[J].Journal of Sound and Vibration,2005,279:857—936.
[2]SONG Y.Modeling,identification and simulation of dynamics of structures with joints and interfaces[D].USA:Ph.D.dissertation,University of Illinois at Urbana-Champaign,2004.
[3]DOHNER J L.White paper:on the development of methodologies for constructing predictive models of structures with joints and interfaces[D].Sandia National Laboratories,2001,SAND2001:1—14.
[4]SEGALMAN D J,BERGMAN L A,EWINS D J.Report on the SNL/NSFinternational workshop on joint mechanics[D].Sandia National Laboratories,2006,1—12(SAND2006).
[5]AHMADIAN H,JALALI H.Generic element formulation for modelling bolted lap joints[J].Mechanical Systems and Signal Processing,2007,21:2 318—2 334.
[6]SEGALMAN D J.Afour-parameter Iwan Model for lap-type joints[J].Transactions of the American Society of Mechanical Engineers Journal of Applied Mechanics,2005,72:752—760.
[7]XUE Y.Developments of joint elements and solution algorithms for dynamic analysis of jointed structures[D].USA:Ph.D.Dissertation,University of Colorado Department of Aerospace Engineering Sciences,2002.
[8]OLDFIELD M,OUYANG H,MOTTERSHEAD J E.Simplified models of bolted joints under harmonic loading[J].Computers and Structures,2005,84:25—33.
[9]MILLER J D,QUINN D D.Atwo-sided interface model for dissipation in structural systems with frictional joints[J].Journal of Sound and Vibration,2009,321(1):201—219.
[10]JALALI H,AHMADIAN H,MOTTERSHEAD J E.Identification of nonlinear bolted lap-joint parameters by force-state mapping[J].International Journal of Solids and Structures,2007,44(25/26):8 087—8 105.
[11]FU Weiping,HUANG Yumei,ZHANG Xueliang,et al.Experimental investigation of dynamic normal characteristics of machined joint surfaces[J].Journal of Vibration and Acoustics,2000,122(4):393—398.
[12]刘耀,黄玉美.机床滚珠导轨中圆柱面-球面结合面静特性分析及试验研究[J].机械工程学报,2013,49(21):25—30.LIU Yao,HUANG Yumei.Theoretical analysis and experimental study on static characteristics of the cylindrical-spherical joint surfaces of linear ball guide on machine tool[J].Chinese Journal of Mechanical Engineering,2013,49(21):25—30.
[13]蔡力钢,李玲,郭铁能,等.基于力状态映射法辨识非线性结合部动态参数[J].机械工程学报,2011,47(7):65—72.CAI Ligang,LI Ling,GUO Tieneng,et al.Identification of nonlinear joint parameters with force-state mapping method[J].Journal of Mechanical Engineering.2011,47(7):65—72.
[14]李玲,蔡安江,蔡力钢,等.基于Bouc-Wen模型辨识结合面动态特性研究[J].振动与冲击,2013,32(20):139—144.LI Ling,CAI Anjiang,CAI Ligang,et al.Dynamic characteristics identification of joint interfaces based on a Bouc-Wen model[J].Journal of Vibration and Shock,2013,32(20):139—144.
[15]胡海岩,王在华.论迟滞与时滞[J].力学学报,2010,42(4):740—746.HU Haiyan,WANG Zaihua.On hysteresis and retardation[J].Chinese Journal of Theoretical and Applied Mechanics,2010,42(4):740—746.
[16]葛世荣,朱华.摩擦学的分形[M].北京:机械工业出版社,2005.GE Shirong,ZHU Hua.Fractal in Tribology[M].Beijing:China Mechine Press,2005.
[17]WANG S,KOMVOPOULOS K.Afractal theory of the interfacial temperature distribution in the slow sliding regime:part II-multiple domains,elastoplastic contacts and applications[J].Journal of Tribology,Transcations of ASME,1994,116(4):824—832.
[18]WANG S,KOMVOPOULOS K.Afractal theory of the interfacial temperature distribution in the slow sliding regime:Part I-elastic contact and heat transfer analysis[J].Journal of Tribology,Transcations of ASME,1994,116(4):812—822.
[19]廖伯瑜,周新民,尹志宏.现代机械动力学及其工程应用[M].北京:机械工业出版社,2004.LIAO Baiyu,ZHOU Xingmin,YIN Zhihong.Modern machine Dynamics and Application[M].Beijing:China Mechine Press,2004.
[20]MINDLIN R D,DERESIEWICZ H.Elastic spheres in contact under varying oblique forces[J].Journal of Applied Mechanics,1953,20(3):327—344.
[21]OLOFSSON U.Cyclic micro-slip under unlubricated conditions[J].Tribology International,1995,28:207—217.
[22]SEGALMAN D J,STARR MJ.Inversion of Masing models via continuous Iwan systems[J].International Journal of Non-Linear Mechanics,2008,43:74—80.
[23]YANG T,FAN HS,LIN S C.Joint stiffness identification using FRFmeasurements[J].Computers and Structures,2003,81:2 549—2 556.
[24]GUO Tieneng,LI Ling,CAI Ligang,et al.Alternative method for identification of the dynamic properties of bolted joints[J].Journal of Mechanical Science and Technology,2012,26(10):3 017—3 027.
Equivalent linear method for hysteresis nonlinear of bolted joints
LI Ling1,CAI An-jiang1,RUAN Xiao-guang1,WANG Zhan-sheng2
(1.School of Mechanical and Electrical Engineering,Xi'an University of Architecture Technology,Xi'an 710055,China;2.Luoyang Institute of Electro-optical Devices,Luoyang 471009,China)
Within engineering application,the modeling and the solution of the bolted joint are very difficult for its strongly nonlinear characteristics and its coupling with other models.In order to facility engineering application,the contact of two rough surfaces of bolted joints can be modeled by a flat,smooth surface in contact with a rough surface in the first place.Secondly,the restoring force model of bolted joints is demonstrated through Masing hypothesis and the force-displacement relationship of bolted joints.Then,suppose that the bolted joints under the condition of the stability excitation and the small vibration amplitude,we obtain the equivalent linearization stiffness and damping model of bolted joints applying the method of averaging.Finally,the laboratorial platform of modal testing and restoring force are established,and the whole structure model is obtained by the equivalent linearization model of bolted joints coupled with finite element model with finite element method.During a cyclic displacement the theoretical model shows good agreement with experimental results.
bolted joints;hysteresis nonlinear characteristics;restoring force model;equivalent linearization models
TH113.1;O322
A
1004-4523(2015)04-560-07
10.16385/j.cnki.issn.1004-4523.2015.04.008
李玲(1981—),男,博士,副教授。电话:13468655809;E-mail:lee_liling@163.com
2014-04-01;
2015-03-12
国家自然科学基金资助项目(51305327,51475352);高等学校博士学科点专项科研基金资助项目(20136120120020)和陕西省教育厅科研计划项目资助(2013JK1033)

