动态子结构法在航天工程中的应用研究

邱吉宝，张正平，李海波，张 忠，韩 丽，任 方

(北京强度环境研究所可靠性与环境工程技术重点实验室，北京100076)

动态子结构法在航天工程中的应用研究

邱吉宝，张正平，李海波，张 忠，韩 丽，任 方

(北京强度环境研究所可靠性与环境工程技术重点实验室，北京100076)

以载荷分析为主要内容，概述动态子结构法在航天工程中的应用。首先采用约束子结构模态综合法与超单元法进行全箭级器箭耦合载荷分析，给出器箭界面加速度条件、运载器和航天器的内部载荷；然后介绍采用航天器基础激励方法与超单元法，依据全箭级器箭耦合载荷分析给出的器箭界面加速度条件，进行航天器级的载荷二次分析，给出航天器的内部载荷，可以证明载荷二次分析所得航天器的内部载荷结果与全箭级器箭耦合载荷分析结果一样。由此说明航天器级载荷二次分析获得结果是可信的，也就是说全箭级器箭耦合载荷分析与航天器级载荷二次分析流程是合理的、可靠的。

结构动力学；模态综合法；子结构法；耦合载荷分析

引 言

结构设计已从静态设计转为静、动态设计。运载火箭的结构设计不能再停留在静态设计水平上，必须采用以结构动力学分析与试验为基础的动态优化设计技术。胡海昌在“加快从静态设计到动态设计的过渡”［1］一文中指出：从本质上来说，卫星结构设计应是一种动态设计。运载火箭和它发射的航天器(包括卫星、飞船、空间运输系统STS、有效载荷等)组成航天飞行器，器箭 (航天器和运载火箭组合的简称)耦合载荷分析是研究航天飞行器结构动态响应的一种理论计算方法，它不是计算火箭所受的气动力、推力等外载荷，而是计算在这些外载荷作用下火箭各部段的内力，航天工程的习惯，把内力计算称为载荷计算。以往多关注结构模态分析，本文多关注动态响应分析。

航天器的设计过程始于以往类似结构的设计经验基础上的载荷初步估计［2-3］。一旦航天器的初步设计及相应的图纸完成，就可建立各子结构动态有限元模型，航天器模型耦合到相应的运载器模型，形成了独特的器箭耦合模型，进行器箭耦合载荷分析。初步设计载荷循环是几个这样载荷循环中的第一个。对于每个全箭级的器箭载荷循环，运载器组织开发的模型，对应发射升空每个事件的运动方程的数值求解，计算系统的响应，给出运载器和航天器的内部载荷，最重要的是给出器箭界面加速度条件［4］，该力学环境条件是进行航天器及部组件结构设计的约束条件，同时也是地面验证试验和可靠性评价的重要依据。该器箭界面加速度条件与航天器载荷发回给航天器组织，进行结构的裕度评估。航天器组织根据器箭界面加速度条件进行载荷二次分析，获得航天器的内部载荷，与作为初步设计阶段计算载荷相对照，评估设计。若有负裕度的区域，则修改结构、重新分析载荷、重新设计，任何结构更改生效之后，更新图纸和有限元模型，以反映这些设计变化。载荷分析整个过程要反复进行多次载荷循环。全箭级器箭耦合载荷分析是大循环，涉及系统各个部门，工作量大，分析结果可靠。但是，一个典型的航天器发展计划仅能有很少几次大循环，而每个全箭级器箭耦合载荷分析后需要进行多次航天器级载荷二次分析小循环。这里自然产生一个问题：采用航天器模型进行载荷二次分析获得结果是否可靠，有多大误差，即由航天器组织根据器箭界面的加速度条件对航天器模型进行载荷二次分析所获得航天器内部加速度(载荷)解，与由运载火箭组织根据器箭耦合载荷分析获得航天器加速度(载荷)解是否一致，是否存在‘过设计'和‘欠设计'问题，是本文侧重研究的问题。

本文以载荷分析为主要内容，概述动态子结构法在航天工程中的应用。首先采用约束子结构模态综合法与超单元法进行全箭级器箭耦合载荷分析，给出器箭界面加速度解析解(称之为器箭界面加速度条件)、运载器和航天器的内部加速度(载荷)解析解；然后介绍采用航天器基础激励方法与超单元法，依据全箭级器箭耦合载荷分析给出的器箭界面加速度条件，进行航天器级的载荷二次分析，给出航天器的内部加速度(载荷)解析解，严格证明了载荷二次分析所得航天器的内部加速度(载荷)解析解结果与全箭级器箭耦合载荷分析给出的加速度(载荷)解析解结果一样。由此说明航天器级载荷二次分析所获得的结果是可信的，不存在‘过计算'、‘欠计算'问题，完善了航天器级载荷二次分析方法。也就是说全箭级器箭耦合载荷分析与航天器级载荷二次分析的循环流程是合理的。

1 运载火箭约束子结构模态综合法

采用动态子结构法计算一个大型复杂结构系统时，首先将整体系统划分为若干子结构。如图1所示，可以将航天飞行器划分为两个子结构：航天器为子结构A，运载火箭为子结构B。

为叙述方便，仅考虑如图1所示两个子结构的简单情况。但其综合方法不难推广到多个子结构情况。

图1 运载火箭结构Fig.1 Structure of launch vehicle

1.1 器箭界面综合方程

自上世纪60年代初Hurty［5］和Gradwell［6］奠定模态综合技术以来，子结构方法已广泛应用于航天航空和各种大型工程领域，是一种复杂结构建模与分析的有效方法。采用这种方法通过模态坐标变换可以把结构动力学问题化为缩聚自由度的问题，从而大大简化了计算，提高了分析效率。约束子结构模态综合法是在航天工程中应用最多的一种［7］。

人们从外场振动测量数据的分析中已发现火箭在飞行过程中的振动环境本质上是多维振动。因而考虑的振动自由度位移响应；XA，XB是多维向量。

子结构A，B的位移解析表达式分别为：

式中 XA表示航天器自由度位移响应；表示航天器内部自由度位移响应；表示器箭界面自由度位移响应；表示运载火箭自由度位移响应；s表示运载火箭内部自由度位移响应；表示器箭界面自由度位移响应；为航天器特征值向量，为相应的模态坐标；为运载火箭特征值向量，为相应的模态坐标；为航天器静约束模态；为运载火箭静约束模态。

采用模态综合法求得系统的特征值和特征值向量，然后，采用的模态叠加法进行响应的叠加。这个过程要进行繁杂冗长的计算。文献［8-9］介绍一种采用器箭界面综合的新方法，导出器箭界面综合方程为

式中 Am为全箭振动器箭界面加速度，方程(2)就是缩聚在器箭连接界面处的全箭动力学方程。MAB(ω)称之为器箭连接界面处结构的视在质量。FAB称之为器箭连接界面处缩聚力向量。方程(2)是器箭界面综合法导出的器箭界面动力学方程，或者称之广义牛顿方程。将航天器子结构自由度nA+m与运载子结构自由度nB+m，减缩为器箭界面上m个自由度的器箭界面综合方程(2)。MA(ω)称之为航天器子结构器箭界面视在质量，MB(ω)称之为运载子结构器箭界面质量。fA称之为航天器子结构器箭界面处缩聚力向量，fB称之为运载子结构器箭界面处缩聚力向量。

已知外载荷

就可以由式(6)求得fA，fB，由式(4)求得FAB。然后由式(2)求得器箭连接界面处的界面加速度响应Am为

式中 Am=-ω2Xm，HAB(ω)=(MAB(ω))-1为器箭连接界面处频响函数。

可以导出全箭振动时航天器响应XA为

AA=-ω2XA，得全箭振动时航天器加速度响应AA为

全箭振动时航天器内部加速度响应AAs为

按动力学方程(2)求得器箭界面处的响应式(8)，然后由式(10)或(11)计算全箭振动时航天器响应。

全箭振动时器箭耦合载荷分析，由式(8)给出器箭界面加速度条件Q为

由式(11)计算给出全箭振动时航天器内部响应AAs为

1.2 航天器模型的基础激励计算方法

单独航天器结构如图1(a)所示。航天器与运载火箭对接界面称之为器箭界面，可以将运载火箭对航天器的作用简化为器箭界面加速度传递，根据运载组织提供的界面加速度条件，采用文献［10-11］介绍的无阻尼系统基础激励的方法求解单独航天器部件的动态响应，进行航天器级载荷分析。考虑如图1(a)所示具有虚拟基础界面的航天器结构，用解析方法，可以将位移幅值向量X'A表示为

公式(14)表明当前自由边界状态结构位移X'A的完备集是约束边界主模态集φ'b加上静约束模态。

文献［10-11］导出结构的基础界面上的动力学方程为

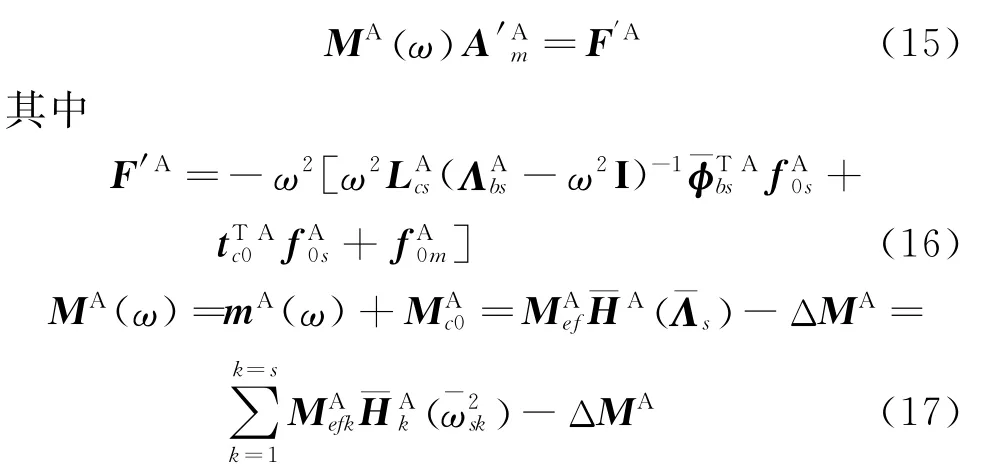
方程(15)中含有界面加速度幅值A'Am、结构的视在质量MA(ω)与界面等效激励力F'A，这是基础激励的动力学方程，或者称之广义牛顿方程。表明可以将n个自由度系统减缩为基础界面上m个自由度基础激励方程(15)。

可以导出位移幅值向量X'A为

1.3 航天器载荷二次分析

现在的问题是在给出的器箭界面加速度条件Q之后，航天器级如何进行载荷二次分析才能给出航天器内部加速度A'As等于全箭振动时航天器内部响应AAs。

航天器载荷分析给出的航天器内部加速度A'As为式(21)与航天器基础界面加速度A'Am为式(18)。现在让航天器基础界面加速度A'Am等于器箭界面加速度条件Q，进行载荷二次分析，则有航天器基础界面加速度A'Am为

则载荷二次分析给出的航天器内部加速度A'As(式(21))化为

这就是说，让航天器基础界面加速度A'Am等于器箭界面加速度条件Q，则有航天器基础界面激励给出的航天器内部响应A'As等于全箭振动时航天器内部响应AAs，再现了全箭振动时航天器内部响应AAs。因而，航天器基础界面激励的载荷二次分析比全箭振动时航天器内部响应分析简化很多，只涉及航天器结构，因而大大节省载荷分析的周期。

式(22)是界面加速度控制，在程序上用界面加速度约束来实现，注意不能采用置大数算法。由式(22)界面加速度控制方程，求得航天器基础界面处缩聚力向量F'A应为

这是基础界面缩聚力控制方程。由此可见，界面加速度控制与界面缩聚力控制本质上是相同的。式(25)的界面缩聚力F'A控制，在程序上用界面缩聚力加载来实现。由于界面缩聚力向量 F'A=Q/HAm(ω)中已经除去航天器基础激励的频响函数HAm(ω)，这与下凹做法是一样的效果。

基础激励的动力学方程(18)中，界面加速度幅值A'Am等于结构的频响函数H'Am(ω)与界面等效激励力F'A乘积，将式(25)基础界面缩聚控制力F'A=Q/H(ω)代入式(18)基础激励的动力学方程，得

频响函数HAm(ω)包含航天器的基础安装边界条件对航天器基础界面加速度A'Am的影响。此式将分子与分母中的航天器基础界面处频响函数HAm(ω)相互削除，这就削去了基础激励边界条件的影响。这就是说，让航天器基础界面加速度A'Am等于器箭界面加速度条件Q，就能削去基础界面处频响函数的影响，也就削去了基础激励边界条件的影响，则有航天器基础界面激励给出式(24)航天器内部响应A'As等于全箭振动时航天器内部响应AAs，再现了全箭振动时航天器内部加速度响应AAs与界面加速度条件Q。

2 运载火箭阻尼系统振动响应分析

考虑如图2所示运载火箭，一般情况为非比例阻尼系统，如果采用非比例阻尼阻尼系统约束模态综合法计算，会导致复杂复数运算。为避开非比例阻尼带来的计算复杂性，这里采用超单元方法分析。首先将运载火箭整体系统划分为若干超单元。如图2所示，可以将运载火箭划分为两个超单元：航天器为超单元A，运载火箭为超单元B。超单元运动方程为

图2 运载火箭结构Fig.2 Structure of launch vehicle

2.1 航天器基础激励振动状态

考虑如图2(a)所示单独航天器结构。进行航天器级载荷分析。按基础界面(m)自由度与非基础界面(s)自由度分块形式超单元方法运动方程，运动方程又可写为

式中 X's表示基础激励中航天器内部自由度位移响应；X'm表示航天器基础界面自由度位移响应；上标'表示单独航天器的基础激励响应；X's，X'm都是多维振动向量。令D=K+iωC-ω2M为动刚度矩阵。则航天器运动方程(27)化为

由式(28)第一方程DssXs+DsmXm=fs得航天器基础界面激励的航天器内部响应X's为

式中 A'm为航天器基础界面加速度，A'm=-ω2X'm，H'(ω)为频响函数，方程(30)就是缩聚在航天器基础界面处的动力学方程。M'(ω)称之为航天器基础界面处结构的视在质量。F'称之为航天器基础界面处缩聚力向量。方程(30)是单独航天器超单元方法导出的基础界面处动力学方程，或者称之广义牛顿方程。

航天器基础激励给出的航天器内部加速度响应A's为

2.2 器箭耦合全箭振动时的航天器振动状态

当采用动态子结构法计算一个大型复杂航天飞行器系统时，首先将运载火箭整体系统划分为若干子结构。如图2元B，作为超单元方法分析。

航天器子结构运动方程为

运载火箭子结构运动方程为

式中 FB表示运载火箭承受的各种载荷。Xs表示全箭振动中航天器内部自由度位移响应；Xm表示全箭振动中运载火箭与航天器的界面自由度位移响应；XB表示运载火箭内部自由度位移响应；则全箭振动过程中的器箭耦合模型运动方程为

由式(36)第一方程DssXs+DsmXm=fs得

由式(36)第三方程DBmXm+DBBXB=fB得

上面两式代入式(36)第二方程DmsXs+DmmXm+DmBXB=fm，得全箭振动时器箭界面处加速度响应Am的解析解为

式中 Am为全箭振动器箭界面加速度，Am=-ω2Xm，H(ω)为频响函数，方程(39)就是缩聚在器箭界面处的全箭动力学方程。M(ω)称之为器箭连接界面处器箭系统结构的视在质量。F称之为器箭界面处缩聚力向量。方程(39)是全箭振动超单元方法导出的器箭界面处动力学方程，或者称之广义牛顿方程。

由式(37)得全箭振动时器航天器内部加速度响应As的解析解为

全箭振动时器箭耦合载荷分析，给出器箭界面处加速度条件Q为

式(43)全箭振动时航天器内部响应AAs化为

2.3 航天器载荷二次分析

在给出的全箭振动时器箭界面加速度条件Q之后，如何进行航天器级的载荷二次分析才能给出航天器内部加速度A's等于全箭振动时航天器内部响应As是要解决的问题。

航天器载荷二次分析给出的航天器内部加速度A's为式(33)与航天器基础界面加速度A'm为式(31)。让航天器基础界面加速度A'm等于器箭界面加速度条件Q，则航天器基础界面加速度A'm为

航天器载荷二次分析给出天器内部加速度A's化为

比较式(47)与(45)，可以看到

由此可以看到，让航天器基础界面加速度A'm等于全箭振动时器箭界面加速度条件Q，则有航天器基础界面激励给出的航天器内部加速度响应A's等于全箭振动时航天器内部加速度响应As，再现了全箭振动时航天器内部加速度响应As。这样，基础激励航天器响应式(46)，(47)再现全箭振动过程航天器响应。因而，航天器基础界面激励的载荷二次分析方法可以大大减少全箭级器箭耦合载荷分析次数，大大节省载荷分析的周期。

式(46)是界面加速度控制。由此求得界面力F'应为

这是基础界面力控制。由此可见，界面加速度控制与界面力控制在本质上是相同的。

式(46)是界面加速度控制，在程序上用界面加速度约束来实现，注意不能采用置大数算法；式(49)是界面力F'控制，在程序上用界面力加载来实现。由于界面力F'=Q/H'(ω)中已经除去航天器基础激励的频响函数H'(ω)，这与下凹做法是一样的效果。

基础激励的动力学方程(31)，界面加速度幅值A'm等于结构的频响函数H'(ω)与界面等效激励力F'A乘积，将式(49)基础界面缩聚控制力F'A=Q/H(ω)代入式(31)基础激励的动力学方程，得

频响函数H'(ω)包含航天器的基础安装边界条件对航天器基础界面加速度A'm的影响。此式将分子与分母中的航天器基础界面处频响函数H'(ω)相互削除，这就削去了基础激励边界条件的影响。这就是说，让航天器基础界面加速度A'm等于器箭界面加速度条件Q，就能削去基础界面处频响函数的影响，也就削去了基础激励边界条件的影响，则有航天器基础界面激励给出式(48)，即航天器内部响应A's等于全箭振动时航天器内部响应As，再现了全箭振动时航天器内部加速度响应As与界面加速度条件Q。

3 总 结

本文以载荷分析为主要内容，概述动态子结构法在航天工程中的应用。

首先对于无阻尼系统采用约束子结构器箭界面综合方法，进行全箭级器箭耦合载荷分析、给出器箭界面加速度条件、运载器和航天器的内部加速度(载荷)解析解；同时介绍依据全箭级器箭耦合载荷分析给出的器箭界面加速度条件，采用单独航天器基础激励方法进行航天器级的载荷二次分析，给出航天器的内部加速度(载荷)解析解，并且证明了所得航天器内部加速度(载荷)解析解结果与全箭级器箭耦合载荷分析所得航天器内部加速度(载荷)解析解结果一样。说明全箭级器箭耦合载荷分析与航天器级的载荷二次分析循环流程的合理性与可靠性。

然后，对于阻尼系统采用超单元法进行全箭级器箭耦合载荷分析，给出器箭界面加速度条件、运载器和航天器的内部加速度(载荷)解析解；同时介绍采用航天器基础激励超单元法，依据全箭级器箭耦合载荷分析给出的器箭界面加速度条件，进行航天器级的载荷二次分析，给出航天器内部加速度(载荷)解析解，也同样证明了载荷二次分析所得航天器内部加速度(载荷)解析解结果与全箭级器箭耦合载荷分析给出的航天器内部加速度(载荷)解析解结果一样。由此说明航天器级载荷二次分析获得结果是可信的，也就是说全箭级器箭耦合载荷分析与航天器级载荷二次分析流程是合理的、可靠的。

由此得到如下结论：

1)有了准确的器箭有限元分析模型和航天器有限元模型，通常由运载火箭组织根据器箭耦合载荷分析获得器箭界面的环境条件；而航天器组织则根据器箭界面的加速度条件对航天器模型采用基础激励方法进行二次分析获得航天器内部加速度(载荷)解。本文采用两种方法说明只要让基础激励航天器界面的输入加速度为全箭振动器箭界面加速度条件，航天器基础激励仿真就会再现了全箭振动过程中航天器内部加速度(载荷)解，不存在‘过设计'和‘欠设计'问题。这样，航天器级载荷二次分析获得结果是可信的，也就是说全箭级器箭耦合载荷分析与航天器级载荷二次分析的循环流程是合理的、可靠的。在设计航天器过程中，根据运载火箭组织在器箭耦合载荷分析中获得器箭界面的环境条件，航天器组织不断修改结构、进行载荷二次分析循环，加快了设计周期；

2)航天器的力学环境条件包括器箭界面环境条件和航天器上部件/分系统的环境条件，器箭界面的环境条件，通常由运载火箭组织根据器箭耦合载荷分析获得；而航天器上细化的环境条件则由航天器组织根据器箭界面的加速度条件对航天器模型采用基础激励方法进行二次分析获得。这里自然提出两个问题：一是由运载火箭组织给出的器箭界面的加速度环境条件是否正确；二是由航天器模型采用基础激励方法进行二次分析获得结果是否可信；上述介绍已经说明航天器级载荷二次分析获得结果是可信的，现在的问题归结为由运载火箭组织给出的器箭界面的加速度环境条件是否正确，如何得到正确的器箭界面加速度条件，是需要认真加以解决的重大问题。器箭界面加速度条件通常是根据多次实际测量的遥测数据或者动力学分析的响应数据，采用统计包络的方法制定的，这导致在共振频率处由包络制定的加速度条件通常远高于真实的加速度环境，产生器箭界面加速度条件的误差。从安全性与可靠性角度出发，传统工程型号研制过程中通常采用直接包络并增加一定安全余量的方法，使得星箭研制总体部门之间以及卫星总体和分系统研制部门之间出现层层加码的现象，导致力学环境条件过于保守。这种误差必须经过细化包络技术，必须认真加以解决的重大问题。

3)根据上面分析，必须进行多维振动分析，进行多维振动试验。运载火箭与航天器结构采用纵、横、扭耦合一体化建模技术，建立的有限元数学模型具有纵、横、扭耦合模态，结构中的每个点的响应都是多维向量。以最简化的运载火箭工程梁模型为例，在器箭界面处是一点连接，连接点处有三向位移加速度与3个转角加速度，界面响应是六维向量，可以简化分解为：纵向振动位移；扭转振动位移；俯仰横向振动位移与转角；偏航横向振动位移与转角。现在振动台振动试验都假定各方向振动互相独立，遥测数据仅测到3个位移加速度，没有遥测3个转角加速度，界面响应遥测数据不全。仅依据三个位移响应数据，应用动力学方程计算出航天器与运载火箭内部的响应与内力，它的误差很大。因而，界面响应数据不全是造成误差很大的一个主要原因。按3个正交方向的振动响应分别包络给出3个正交试验条件，以3个正交轴依次进行的单轴振动试验近似等效飞行过程中的多维振动环境，这样试验和飞行环境的差异很大，需要通过加大试验量级和时间予以适当补偿。尽管这种振动环境考核方式在航天工程中得到了广泛应用，但在应用过程中也暴露出一些严重的缺陷，可以说明现有器箭界面环境条件局限性。仅用3个位移响应数据作为控制条件进行振动试验，是造成“过试验”与“欠试验”的主要原因。对于横向振动问题朱礼文［12］做过研究，指出：在星箭界面横向振动相同的条件下，比较升空过程横向振动与振动台横向振动(仿真计算是已知卫星基础界面的加速度-时间历程，求结构的动响应，即本文介绍的基础激励。)的两种振动状态卫星顶点的动响应，结果毫无共同点。这是由于升空过程星箭界面有角运动，而地面试验却限制界面角运动。在仿升空状态的计算中，确定了与星箭界面线运动相关的角运动，并以此作为基础激励补充条件，再进行地面振动试验仿真计算，此时卫星顶点动响应与升空状态一致。

［1］胡海昌.加快从静态设计到动态设计的过渡［J］.宇航学报，1980，1(2)：103—106.Hu Haichang.Accelerate the transition from a static to a dynamic design design［J］.Journal of Astronautics，1980，1(2)：103—106.

［2］Kabe M，Kim MC，Spiekermann C E. Loads analysis for national security space missions［J］.Rocket Science，2004，5(1)：(10.3.Winter 2004)

［3］Flanigan C C.先进的耦合载荷分析——MSC/NASTRAN分析［M］.MSC/NASTRAN World Users Conference，1991.

［4］马兴瑞，韩增尧，邹元杰，等.航天器力学环境分析与条件设计研究进展［J］.宇航学报，2012，33(1)：1-12.MAXing-rui，HAN Zeng-yao，ZOU Yuan-jie，et al.Review and assessment of spacecraft mechanical environments analysis and specification determination［J］.Journal of Astronautics，2012，33(1).1—12.

［5］Hurty W C.Vibration of structure systems by component mode synthesis［J］.Jour.Engr.Div.，ASCE，1960，86：51—59.

［6］Gladwell ML.Branch mode analysis of vibrating systems［J］.J.Sound Vibration，1960，1：41—59.

［7］Craig R R，Bampton MC.Coupling of substructures for dynamic analysis［J］.AIAAJournal，1968，6：1 313—1 319.

［8］邱吉宝，张正平，李海波.航天器与运载火箭耦合分析相关技术研究进展［J］.力学进展，2012，42(4)：416—436.Qiu Jibao，Zhang Zhengping，Li Haibo，Rogresses on research into coupled analysis technology for space vehicle launch vehicles［J］.Advances in Mechanics，2012，42(4)：416—436.

［9］邱吉宝，张正平，李海波，等.星箭耦合动态响应分析新方法研究［J］.强度与环境，2011，38(3)：1—9.Qiu Jibao，Zhang Zhengping，Li Haibo，et al.Astudy of dynamic response analysis new method for coupled satellite/launch vehicle［J］.Structure&Environment Engineering，2011，38(3)：1—9.

［10］邱吉宝，张正平，黄波，等.基础激励结构动力学问题求解新方法［A］.结构动力学专业委员会2007年研讨会［C］.2007：46—60.Qiu Jibao，Zhang Zhengping，Huang Bo，et al.The new method solving the structure dynamics problem on excited by base［A］.Structural Dynamics Professional Committee 2007 Symposium［C］.2007：46—60.

［11］邱吉宝，向树红，张正平.计算结构动力学［M］.合肥：中国科学技术大学出版社，2009.Qiu Jibao，Xiang Shuhong，Zhang Zhengping，Computational Structural Dynamics［M］.Hefei：University Press of Science and Technology of China，2009.

［12］朱斯岩，朱礼文.航天器升空过程振动环境的地面试验条件［J］.中国科学E辑：技术科学，2012，42(10)：1 103—1 242.Zhu S Y，Zhu L W.Vibration test condition for spacecraft lift-off environment［J］.Sci.China Tech.Sci.，2012，42(10)：1 103—1 242.

Applications of the dynamic substructure method for aerospace engineering

QIU Ji-bao，ZHANG Zheng-ping，LI Hai-bo，ZHANG Zhong，HAN Li，REN Fang
(Science and Technology on Reliability and Environment Engineering Laboratory，Beijing Institute of Structure and Environment Engineering，Beijing 100076，China)

This paper demonstrates the application of the dynamic substructure method in the aerospace engineering.Our main focus is on the load analysis.First，the restraint modal synthesis method and the ultra-element method are applied to perform coupled loads analysis of a complete launch vehicle that is coupled with a spacecraft.As a result，the internal loads for a launch vehicle and its spacecraft，as well as the acceleration conditions of the interface between the spacecraft and the launch vehicle，are obtained.Second，based excitation approach and the ultra-element method for spacecraft，using the derived internal loads by the acceleration conditions of the interface between the spacecraft and the launch vehicle，to perform a secondary load analysis.It is proved that the internal load of the spacecraft that obtained from the secondary load analysis is consistent with the load obtained from the complete launch vehicle.Therefore，the two steps load analysis approach demonstrated in the paper can be considered as a reliable and robust approach for coupled load analysis.

structural dynamics；modal synthesis method；substructure method；coupled load analysis

V414.1

A

1004-4523(2015)04-0510-08

10.16385/j.cnki.issn.1004-4523.2015.04.002

邱吉宝(1938—)，男，研究员。电话：(010)68384534；E-mail：qiujb1@163.com

2013-02-25

：2015-03-10

国家重大基础研究项目(613133)和国家自然科学基金资助项目(11172046)