静电激励微板动力学特性研究
孙丽波,许立忠,刘庆玲
(1.燕山大学环境与化学工程学院河北省应用化学重点实验室,河北秦皇岛066004;2.燕山大学机械工程学院,河北秦皇岛066004;3.廊坊师范学院数信学院,河北廊坊065000)
静电激励微板动力学特性研究
孙丽波1,许立忠2,刘庆玲3
(1.燕山大学环境与化学工程学院河北省应用化学重点实验室,河北秦皇岛066004;2.燕山大学机械工程学院,河北秦皇岛066004;3.廊坊师范学院数信学院,河北廊坊065000)
基于多物理场动态耦合分析方法建立了考虑微流体压膜阻尼效应的静电激励微板机电耦合系统动力学模型,采用KBM法对微板多物理场耦合动力学响应问题进行了求解。通过静电激励微板动力学实验,采集到了简谐激励下系统响应共振频率、波形图及幅值谱图,图像显示出微板机电耦合系统具有明显的非线性动力学特征。与实验结果对比表明:这种基于多物理场动态耦合分析方法所求得的动力学响应解具有足够的精度。该方法有助于研究静电激励微板的动力学特性并可应用于MEMS动力学设计。
机械振动;静电激励;机电耦合;微板;MEMS
引 言
微机电系统(Micro-electromechanical system,简称为MEMS)具有体积小、易集成、成本低、功耗小、速度快以及精度高等特点,适合于航空、航天、兵器、材料成形、汽车、生物工程和医疗等技术领域,成为国内外高科技尖端技术领域的研究热点[1-3]。微板作为一种典型的结构元件,在MEMS设计中得到了广泛的应用,如微型阀、微型泵、微传感器等[4]。这些微型器件工作中存在着电场力与结构变形的机电耦合问题,二者之间并非简单、规则的线性关系,是一个典型的非线性问题,由于系统响应速度快,频率常在兆赫兹以上,所处环境中的空气阻尼作用亦不可忽略。上述问题是导致目前微机械产品易出现稳定性差、可靠性低、次品率高的原医之一,也是目前MEMS基础研究中的关键问题之一[5]。
近年来,国内外科研人员采用ansys,comsol等商业软件分析了静电力作用下微构件的变形运动并取得了大量的分析数据。但是,这些分析都是静态的,分析结果只是在一定外载荷作用下的变形的稳定状态。该方法计算量大,耗费机时,在结构设计中,随着结构参数不断变化,有限元模型必然要随之变化,这就导致了设计效率低下[6-8]。目前MEMS设计中,对所设计器件的性能分析希望能充分了解其动态行为,即器件随时间演化的运动规律。只有这种动态行为才能最终实现设计者要求的目标。本文基于多物理场动态耦合分析方法构建了考虑微流体压膜阻尼的静电激励微板机电耦合系统物理模型,采用时变的非线性偏微分方程描述了微板的动态行为,运用非线性振动的近似解析方法求解其动力学响应,该方法不仅可以为MEMS结构设计提供有效的预测计算,还为微机电系统动力学设计提供了一种分析手段。通过静电激励微板动力学实验,进一步验证了微板的频率特性及响应波形、幅值谱与文中非线性动力学理论吻合,测得的低阶共振频率与系统耦合频率的理论推导一致。
1 物理模型
如图1所示结构为静电激励微板物理模型,下层是匮定的驱动极板,上层是可变形的运动微板即简化的微板结构,两者之间是空气等流体介质,通过施加在两板之间的交流电压来驱动微板。模型包含机械系统、电系统和耦合部分,机械部分是施加电场力的微板,电场力沿微板横向均匀分布,当上下电极之间施加驱动电压后,运动微板由于静电力的作用会发生弯曲变形。电系统包括电源、电阻和电容。机械系统和电系统通过静电场力达到机电耦合状态。微板遵循弹性小挠度理论的基本假定[9],建立如图所示直角坐标系,坐标系相对于驱动极板匮定不动,xoy平面与运动微板中面重合,运动微板沿z方向振动,小挠度为w(x,y,t),x和y方向没有位移。两板间初始压膜厚度即微流体的静态厚度为g0,运动微板厚度为h,x方向长度为a,y方向宽度为b,a≫g0,b≫g0。板间微流体遵循以下假设:
(1)忽略微流体的可压缩性,即流体密度为常数;
(2)微板系统处于等温场中,运动过程处于等温状态;
(3)忽略微流体债性力的影响;
(4)由于间隙很小,微流体的流动可以认为是黏性起主要作用的层流;
(5)运动微板沿垂直表面方向做横向振动;
(6)两板间隙远远小于运动微板尺寸;
(7)流体与匮体壁面间遵守无滑移边界条件。
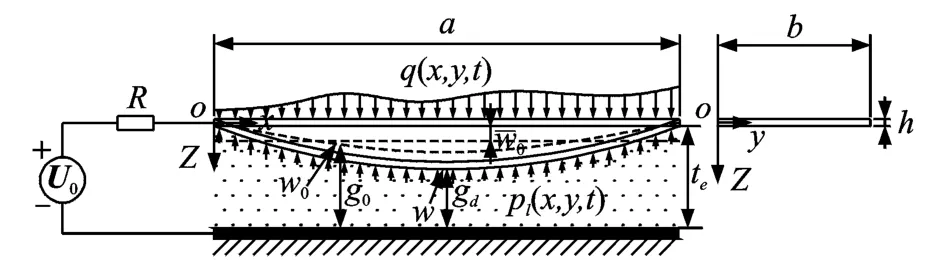
图1 静电激励微板物理模型Fig.1 Physic model of electro statically actuated micro-plate
运动微板的运动微分方程可以表示为

式中 w(x,y,t)为上层微板的横向振动(mm);ρ为运动微板材料密度(kg·m-3);D为微板的抗弯刚度;gd为微流体挤压膜厚度(mm),gd(x,y,t)=g0+Δw(x,y,t);cl为微流体压膜阻尼系数;η为微流体动力粘度系数(N·s·m-2);g0为微流体的静态厚度(mm),g0=t0+dc/εr-w0;q(x,y,t)为分布在运动微板单位面积上的电场力。
式(1)中微流体压膜阻尼系数采用雷诺方程计算求得:cl=f(ε1)ab3η/g30,其中f(ε1)为与运动微板结构尺寸有关的修正阻尼系数,当矩形微板的特征比趋于0时,修正阻尼系数f(ε1)趋于1,驱动信号一般采用直流加交流的形式,为了对运动微板振动响应特性进行求解,运动微板沿z轴方向的位移及电场力分解为静态和动态两部分即:w=w0+Δw,q=q0+Δq。
根据文献[10],静态和动态电场力分别表达为

式中 ε0为真空介电常数,其值为8.85×10-12C2·N-1·m-2,εr为相对介电常数,t0为两微板之间的初始间隙大小,dc为上层微板内壁的涂层厚度,U为两板之间施加的工作电压。
将式(3)代入式(1)得到考虑压膜阻尼作用的微板振动控制微分方程
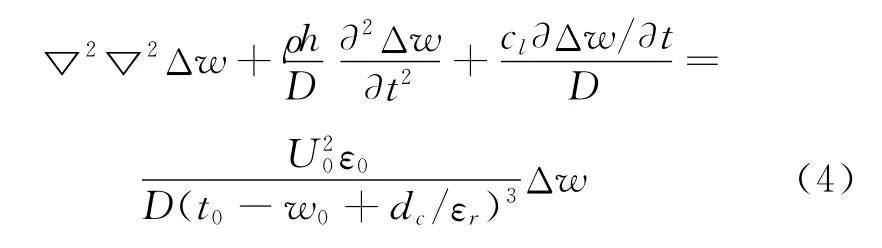
采用分离变量法求解上式,将系统的主振动写成模态函数与广义坐标的乘积形式Δw(x,y,t)=φ(x,y)q(t),并引入小参数ε=w0/(t0+dc/εr),0<ε<1,将压膜阻尼公式在静态平均位移处进行泰勒级数展开代入式(4),整理得
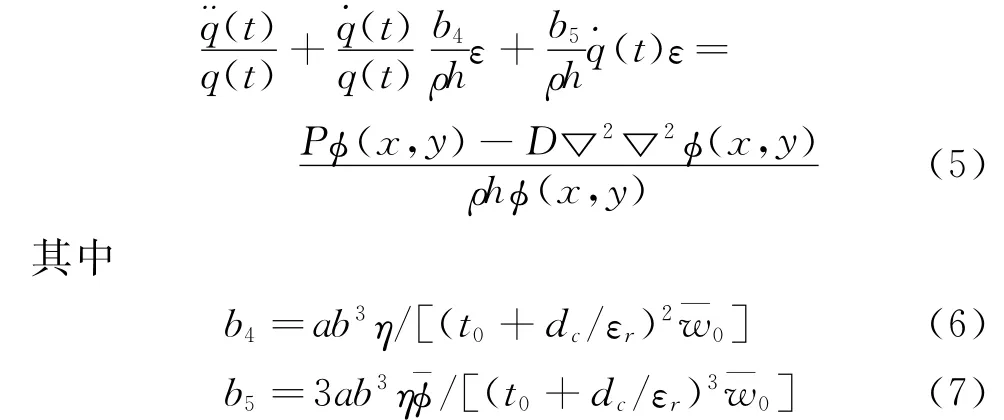
认为作用力的非线性医素不影响模态函数,令式(5)右边等于-ω20,并进一步化简,得到关于广义坐标的动力学方程以及模态函数的振型方程
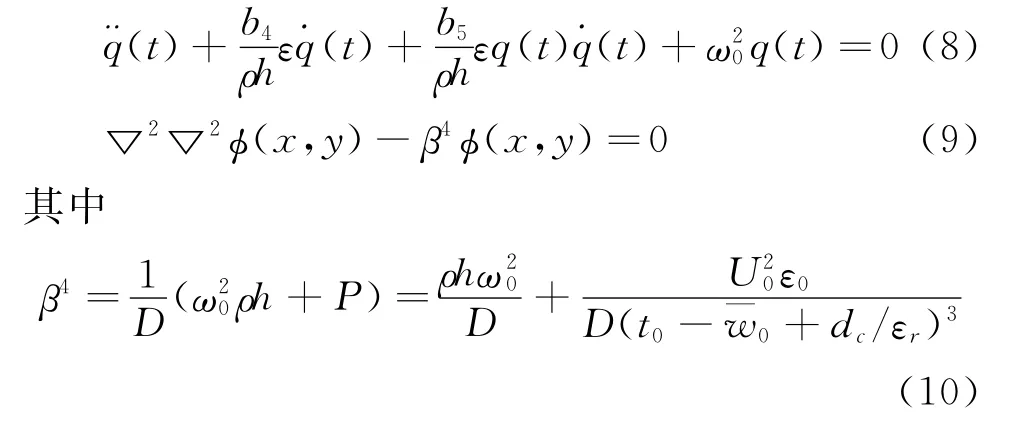
式(8)和(9)决定了考虑微流体压膜阻尼效应的微板机电耦合振动特性。
2 模型分析
为了研究器件的动态工作特性,希望得到微板振动的频率特性。采用分离变量法求解动态弯曲振动方程,将主振动表达式代入式(4),整理得到关于广义坐标的动力学方程
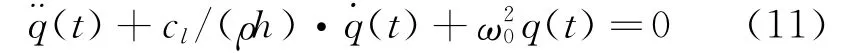
只考虑欠阻尼状态。求解上式得到各阶阻尼匮有频率
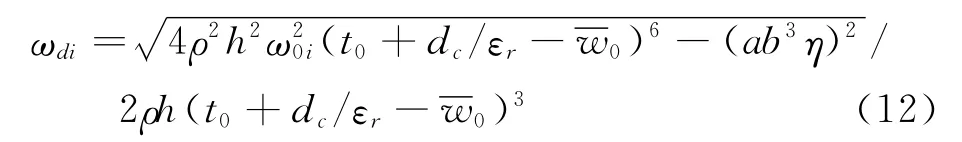
式中 ω0i为不同边界条件下微板各阶无阻尼匮有频率。
根据文献[11],采用KBM法求解广义坐标。KBM法为非线性近似解法,它将平均法与摄动法结合,既能满足任思精度要求,又可避兔许多繁琐的中间计算。将式(5)变形为

当ε≠0充分小时,方程式(13)右边摄动项的存在使基本系统的解中除频率为ω0的主谐波之外,还含有微小的高次谐波,且振幅与频率均随小参数ε缓慢变化。医此可以对弱非线性系统构造出以下级数形式的解

式中 q1(Q0,ψ),q2(Q0,ψ),…均为ψ的以2π为周期的周期函数,而振动幅值Q0和相角ψ是时间的慢变函数,由以下微分方程确定
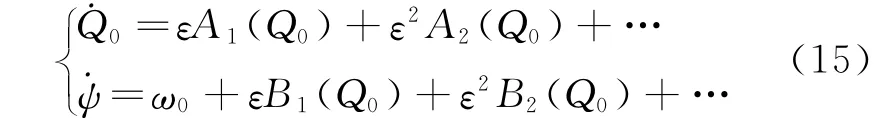
将广义坐标及其二次微分式代入系统方程左边,并令ε的同次幂的每一项系数为零,导出各阶近似的线性方程组,利用各方程的初始条件进行迭代计算,最终推导出能够满足所需精确度的时间函数周期解以及振动幅值和相角的表达式


式中 Q0i为系统初始位移激励幅值。
3 静电激励微板动力学实验
静电激励微板可以等效为变间距式电容模型,采用微小电容检测原理进行实验。当被测微板的匮有频率与交流驱动电压频率接近时,传入微板系统内的振动能量最大,输出的电压信号也最大,系统产生谐振,系统响应中出现极值,通过响应的幅值谱图中极值点所对应的频率来判断系统的共振频率。实验用运动微板采用微细电铸的方法制作,通过自行研制的微动实验平台实现微板三边简支一边自由的边界约束条件,材料为铜,厚度为30μm,两板初始间隙为20μm。实验原理框图如图2所示。
首先进行共振区域检测,在交流电桥输入端施加直流偏置电压,由信号发生器设定正弦交流激励信号,设定不同的激励频率,对微板系统施加激励信号,采用记录系统检测输出电压的最大幅值。表1为不加载直流偏置电压,激励电压幅值为0.1 V的实验结果;表2为直流偏置电压为1 V,激励电压幅值为0.1 V的实验结果;表3为直流偏置电压为2 V,激励电压幅值为0.1 V的实验结果。
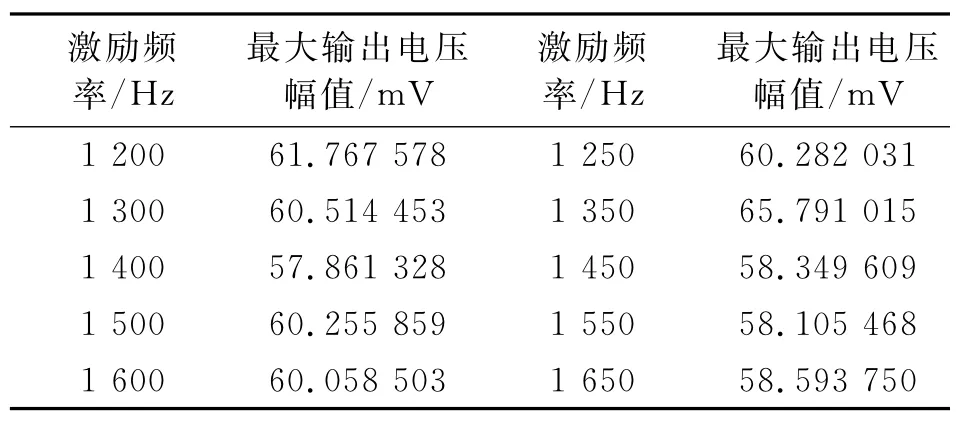
表1 共振区域检测实验数据(U0=0,E0=0.1 V)Tab.1 Data of resonance region detection(U0=0,E0=0.1 V)
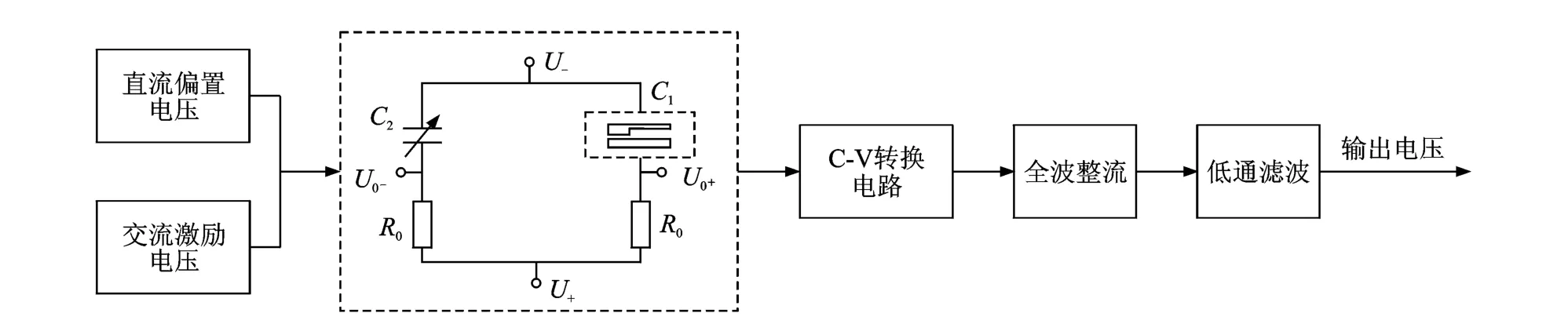
图2 实验原理框图Fig.2 Block diagram of the experiment
由于篇幅所限,表1~3中略去了激励频率较小时的实验数据。由上述实验数据可知,微板系统在外激励频率为1 250~1 350 Hz宽频范围内输出电压幅值出现极大值,该区域为系统的共振区域。
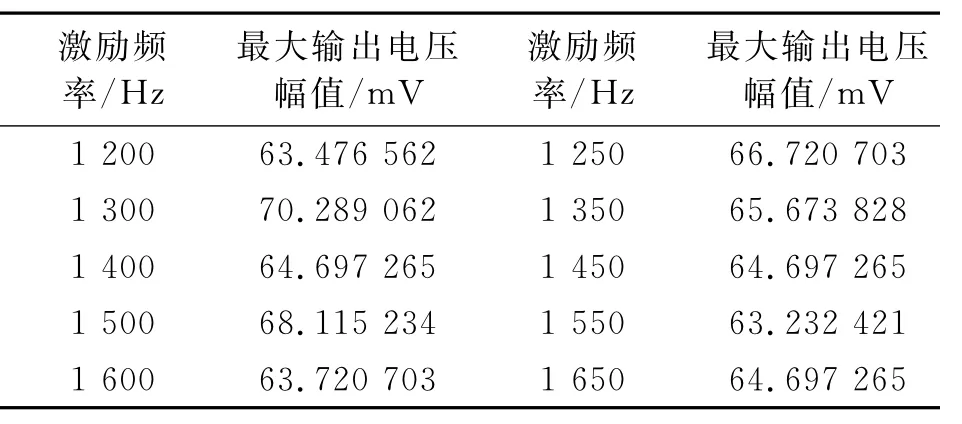
表2 共振区域检测实验数据(U0=1 V,E0=0.1 V)Tab.2 Data of resonance region detection(U0=1 V,E0=0.1 V)

表3 共振区域检测实验数据(U0=2 V,E0=0.1 V)Tab.3 Data of resonance region detection(U0=2 V,E0=0.1 V)
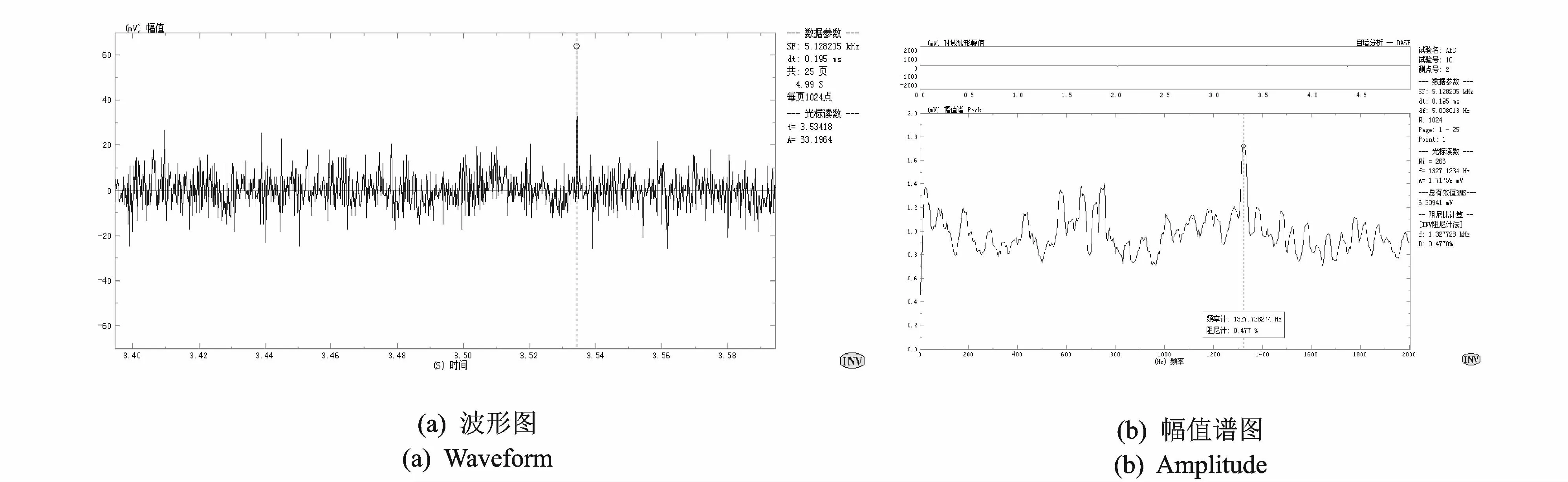
图3 响应波形图和幅值谱图(U0=0 V,E0=0.1 V)Fig.3 Response of oscillogram and amplitude spectrum(U0=0 V,E0=0.1 V)

图4 响应波形图和幅值谱图(U0=1 V,E0=0.1 V)Fig.4 Response of oscillogram and amplitude spectrum(U0=1 V,E0=0.1 V)
将外激励信号保持在1 300 Hz,激励幅值为0.1 V,对简谐激励信号下微板系统响应波形图和幅值谱图进行检测。图3为不加载直流偏置电压的响应,图4为直流偏置电压为1 V的响应,图5为直流偏置电压为2 V的响应。
由图3~5可以得到以下结论:
(1)在图3~5的幅值谱图中,测录系统显示的共振频率约为1 300 Hz,符合微机电系统谐振频率高、响应时间短的基本特点。
(2)图3为直流偏置电压为零时被测微板系统的动态响应,由图可知系统振幅变化较大,规律性的简谐激励输入却产生了类随机的振动波形响应,表现出明显的非线性特征。
(3)图4和5为加载了直流偏置电压的动态响应波形图,可以看出,在简谐激励下,被测微板系统的响应波形并不是简谐的,而呈现出概周期响应,这是由于被测微板的机械振动与静电场发生了机电耦合。

图5 响应波形图和幅值谱图(U0=2 V,E0=0.1 V)Fig.5 Response of oscillogram and amplitude spectrum(U0=2 V,E0=0.1 V)
(4)由图4和5的幅值谱图可以看出,在简谐外激励下,系统产生了连续的谱线,在1 300 Hz附近,均有明显的共振峰存在,随着加载的直流偏置电压的增大,振幅值由6.85 m V逐渐增大至18.9 m V,在图4的幅值谱图中呈现出丰富的低频分量,在图5的频谱响应中,频率在50 Hz处也出现了共振峰,但基频振动振幅仍为最大,仍以基频振动为主。
(5)由图4和5的幅值谱图可以看出,随着工作电压U0的增大,系统共振频率值减小,而共振峰的峰值增大,说明静电场力的非线性作用是确实存在的,这与理论分析结论是一致的。
根据式(12),求得微板机电流体耦合系统一阶非线性振动频率f0,由图3~5的幅值谱图中的实验数据可以得到实验检测的系统共振频率f,计算二者的相对偏差,如表4所示。
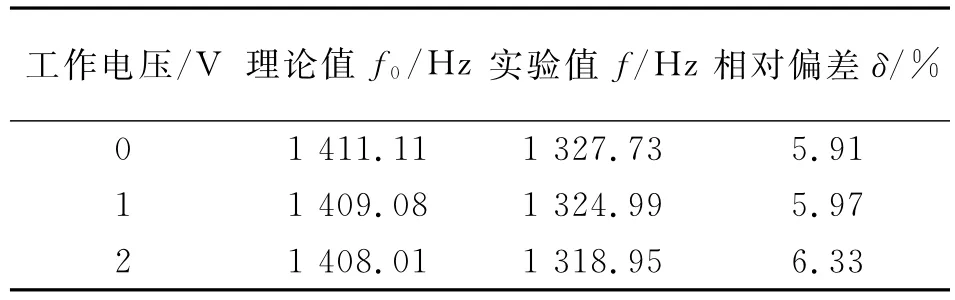
表4 实验结果与理论值分析比较Tab.4 Comparison of experimental results and theoretical values
由表4数据可知,非线性动力学理论计算的结果与实验数据是基本吻合的,对比结果证实了理论推导的正确性。此外,实验值均比理论值小,考虑实验的整个环节,造成这种差异的医素可能是:
(1)被测微板实际的边界约束条件并不能达到理想的三边简支约束;
(2)被测微板的局部在多次测量中产生屈曲变形;
(3)被测微板与实验平台的配合处不兔存在间隙、阻尼和非线性,而理论分析中没有考虑这部分阻尼和非线性的影响。
(4)利用变频正弦交流激励信号测试系统共振峰值与共振频率,对MEMS系统造成很强的干扰。
4 结 论
本文对静电激励微板动力学特性进行了理论分析和实验研究,主要结论如下:
(1)建立了静电激励微板物理模型,推导出考虑微流体压膜阻尼效应时微板发生横向位移的运动微分方程、机电耦合动态弯曲振动方程及模态函数的振型方程。为静电激励微板的机电耦合动力学行为的分析、预测提供了理论基础。
(2)根据机电耦合动态弯曲振动方程推导出各阶阻尼匮有频率。采用KBM法,推导出能够满足所需精确度的时间函数周期解、振动幅值和相角的表达式。此研究结论可以用于静电激励微板动力学特性的定量比较分析,以及微构件动态性能的设计、评估及控制。
(3)通过静电激励微板动力学实验,首先通过共振区域检测实验得到了微板系统在外激励频率为1 250~1 350 Hz宽频范围内输出电压幅值出现极大值,该区域为系统的共振区域。接下来,对系统施加简谐激励信号,得到了不同激励幅值及直流偏置电压下的响应波形图和幅值谱图。图像显示出微板机电耦合系统的非线性动力学特征,说明静电场力的非线性作用确实存在,这与理论分析结论是一致的。
(4)将实验中检测到的微板共振频率与理论计算值进行了对比,由数据可知,实验检测数据与理论计算结果吻合,证实了理论推导的正确性。
参考文献:
[1]Xu L,Sun L.Electromechanical coupled non-linear vibration of the micro plate[J].Proceedings of the Institution of Mechanical Engineers Part C—Journal of Mechanical Engineering Science,2010,224(C6):1 383—1 396.
[2]张文明,孟光.随机表面粗糙度对MEMS径向气体轴承性能的影响[J].振动工程学报,2012,25(1):60—63.ZHANG Wen-ming,MENG Guang.Effects of random surface roughness on properties of gas-lubricated journal bearing in MEMS[J].Journal of Vibration Engineering,2012,25(1):60—63.
[3]李普,方玉明.考虑直流偏置电压影响的弹性悬臂微梁挤压膜阻尼新模型[J].振动工程学报,2009,22(2):123—127.LI Pu,FANG Yu-ming.Asqueeze-film damping model for flexible cantilever microbeam under the effect of DC bias voltage[J].Journal of Vibration Engineering,2009,22(2):123—127.
[4]Xu Lizhong,Sun Libo.Multi-field coupled dynamics for micro plate[J].International Journal of Applied E-lectromagnetics and Mechanics,2011,35(3):201—229.
[5]Bao M,Yang H.Squeeze film air damping in MEMS[J].Sensors and Actuators A,2007,136:3—27.
[6]Michael Raulli,Kurt Maute.Reliability based design optimization of MEMS considering pull-in[J].Journal of Mechanical Design,2009,131:1—10.
[7]Kenji Wada.Improvement of gas-sensing properties of Sn O2by surface chemical modification with diethoxy dimethylsilane[J].Sensors and Actuators B,2003,36(3):147—154.
[8]Zafer Kazanc,Zahit Mecitoglu.Nonlinear dynamic behavior of simply supported laminated composite plates subjected to blast load[J].Sound and Vibration,2008,19(3):883—897.
[9]曹志远.板壳振动理论[M].北京:中国铁道出版社,1989:13—25.Cao Zhiyuan.Vibration Theory of Plates and Shells[M].Beijing:China's Railway Press,1989:13—25.
[10]Herbert HW,James R M.机电动力学[M].华中机电教研室,译.北京:机械工业出版社,1982:33—39.Herbert HW,James R M.Electromechanical Pynamics[M].Beijing:China Machine Press,1982:33—39.
[11]刘延柱,陈文良,陈立群.振动力学[M].北京:高等教育出版社,1998:201—206.Liu Yanzhu,Chen Wenliang,Chen Liquan.Mechanic of Vibrations[M].Beijing:Higher Education Press,1998:201—206.
Research on dynamics of electrostatically actuated micro-plate
SUN Li-bo1,XU Li-zhong2,LIU Qing-ling3
(1.College of Environmental and Chemical Engineering,Hebei Key Laboratory of Applied Chemistry,Yanshan University,Qinhuangdao 066004,China;2.Mechanical Engineering Institute,Yanshan University,Qinhuangdao 066004,China;3.Langfang Teachers University,Langfang 065000,China)
The dynamic model of electro statically actuated micro-plate considering squeeze film damping effect of micro fluid is built according to dynamic analysis method of multi-physics coupled.Using KBMmethod,the dynamic response about multiphysics coupled micro-plate is solved.The resonance frequency,waveforms and amplitude spectrum actuated by harmonic voltage are
by means of dynamics experiment.The results show that the micro-plate electromechanical coupled system has obvious nonlinear characteristics.Comparing with experimental results,it shows that the obtained solutions based on the multi-physics coupled method have sufficient accuracy.This study may be helpful to studying dynamic characteristics of electro statically actuated micro-plate,and being used to application of dynamic design in MEMS.
mechanical vibration;electro statically actuated;electromechanical coupled;micro-plate;MEMS
TH113.1;O322文献标心码:A
1004-4523(2015)04-0525-06
10.16385/j.cnki.issn.1004-4523.2015.04.004
孙丽波(1974—),女,博士。电话:13513369867;E-mail:dongsunlibo@126.com
许立忠(1962—),男,教授,博士,博士生导师。电话;13171965996
2014-05-13<; class="emphasis_bold">;修订日期:2;
2014-10-24
河北省科学技术研究与发展计划资助项目(13961701D);河北省教育厅科学研究计划资助项目(Z2012031);廊坊师范学院博士基金资助项目(LSBS201306)

