基于MRF与纹理特征的图像深度信息估计

陈婷婷，张立志，赵志杰，孙华东，金雪松

(哈尔滨商业大学计算机与信息工程学院，哈尔滨150028)

三维视频能够给观众带来身临其境的感觉，受到越来越多的关注和青睐，自2010年以来，三维显示设备迅速普及[1].三维显示离不开三维显示内容的制作，传统的二维片源不适用于三维显示，需要制作满足三维显示的内容.三维显示内容的制作主要有21种方法:一种是利用专用的视频采集设备来获取[2]，但是这种方法价格昂贵.另一种方法是通过深度信息的获取把二维片源转换成适合三维显示的内容，由于大量传统的二维片源的存在，使得二维图像深度信息提取的研究具有重大意义.

研究者在分析人类生理和心理视觉的基础上，寻找许多深度线索.深度线索的获取方法大体可分为两类，即多目视觉线索和单目视觉线索.多目深度线索取自用多路相机拍摄的多幅场景图像或用单路相机拍摄的动态多幅场景图像，而单目深度线索取自单幅图像.场景深度是指在空间上场景对象与图像物理成像焦平面的实际距离[3].二维场景图像的纹理变化、纹理梯度能给人们提供良好的深度感知线索，通过比较一纹理区域在不同尺度下的位置、大小、方向，估算出纹理区域的相对位置关系，进而可得到相应纹理区域的场景深度.Knorr等提出了利用图像纹理梯度线索提取深度的方法[4]，该方法采用了KLT和E－矩阵对图像进行跟踪与分割，通过自校准、稀疏映射、密集映射等方法实现深度估计.由于线索单一，虽然室外场景的转换得到了较好的重建质量，但是对室内场景图像效果较差.Malik[5]，Saxena[6－7]等人，根据景物对象在不同深度上存在着纹理及阴影差异，通过建立马尔科夫随机场(markov random field－MRF)模型，监督学习方法训练参数，进而估计场景图像深度.该方法有相对理想的效果，但建模时需要大量的训练样本，训练过程较复杂.

基于对纹理渐变特征及优化算法的研究，提出了一种基于MRF的多尺度纹理特征深度估计方法.该方法利用MRF局部区域之间的依赖约束关系，以及Laws滤波器所获取的二维场景图像多尺度纹理能量信息，来描述二维场景图像深度信息.

1 纹理特征提取

纹理一般指人们所观察到图像中像素的灰度变化规律，习惯上把图像中这种局部不规则的，而在宏观上有规律的特性称之为纹理.在数字图像分析中将描述这种灰度变化规律的数字特征称为图像的纹理特征[8].

Laws滤波器作为一种典型的纹理分析手段，在图像纹理能量测度方面有着广泛的应用.它能够从图像边缘、梯度、点等方面有效的分析二维场景图像的纹理特征.

1.1 Laws滤波器

对于Laws滤波模板的选择，Laws进行了深入的研究.他定义了一维滤波模板后，通过卷积形成一系列一维、二维滤波模板，用于检测和度量纹理的结构信息[9].本方法通过一维基础滤波模板卷积成5阶Laws模板，5阶Laws模版向量如下:

模板中，L1表示边缘特征，L2表示灰度特征，L3表示点特征，L4表示涟漪特征，L5表示波特征.把这5个模板分别作为行向量与列向量互相卷积，可以合成25个阶二维的Laws滤波器模板1≤p≤5，1≤q≤5，下例是L1与L4卷积合成的滤波器模版:

其中:将图像分成固定大小的宏块B，(x，y)∈B表示块内的像素点的位置，I(x，y)表示该位置像素值，用Laws滤波器对每一宏块进行卷积，可获得任一宏块B的纹理能量特征E.

该纹理能量特征值反映了宏块在边缘、梯度、点方面的特征，由于宏块在不同尺度下呈现不同的纹理能量值，可以根据纹理能量值的变化，来估计宏块的深度信息.

1.2 多尺度纹理特征

二维场景图像是三维场景在二维平面上的投影.因此，在二维成像过程中会丢失三维信息.局部纹理特征并不能够完全正确估计场景对象某一宏块的深度值，有必要引入其他的局部特征或全局特征.不同对象在不同尺度表现出的分辨率不同，如蓝天在不同尺度表现出的分辨率相同，而具有纹理的草地就表现出不同的分辨率.同一对象在不同尺度的相对大小不同，邻域关系也不同.同一景物对象，在近处就表现的尺度大些，在远处就表现的尺度小些，如图1所示.

图1 多尺度图像的能量测度

尺度空间的思想最早于1962年提出，到20世纪80年代，尺度空间方法逐渐得到关注并进入快速发展阶段[3].把多尺度空间思想应用到图像的纹理能量分析中，可以用来估计二维场景图像的深度信息.如图2所示，每一宏块的上、下、左、右四个相邻的宏块纹理能量均作为该宏块的纹理能量信息特征，用来约束相邻宏块之间深度的依赖关系.

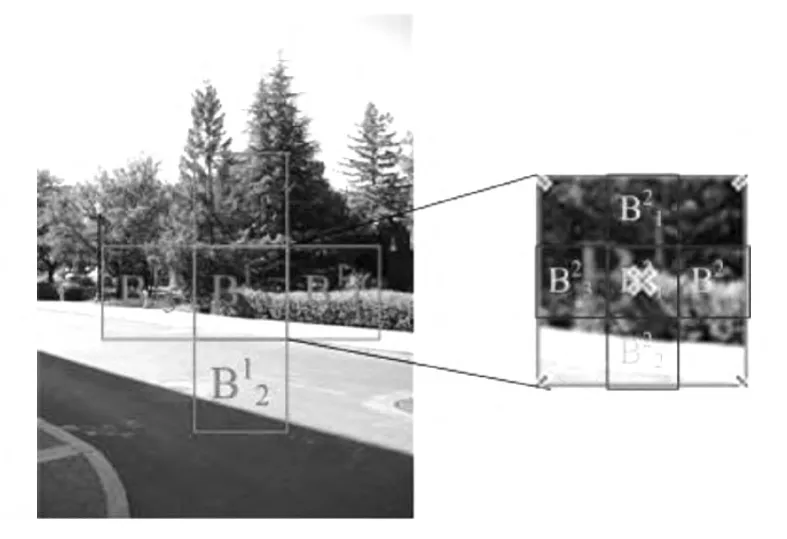
图2 宏块多尺度特征

2 MRF算法模型

MRF理论提供了直接的方法以概率来描述图像像素具有的空间相关特性，MRF与Gibbs分布等价性的提出极大地推广了其在数字图像处理中的应用.随机场X的Gibbs分布可描述为式(2)所示[3].

其中:Z是归一化常数，U(x)是能量函数，是基团的能量的总和.

Vc(x)的取值取决于基团c的势函数.T是温度常量，较高的温度将使得所有配置的概率趋向于相等，使吉布斯分布趋近均匀分布.相反，较低的温度将使吉布斯分布函数向峰值收缩，因而温度常量可以用来控制曲线的形状.

二维MRF能够很好的表现图像中像素之间的空间关系.我们可以把二维场景图像看成一个二维MRF.对于任一宏块，都有相邻或间接相联系的宏块与之依赖约束.这样，每一个独立的宏块都可以用一组与之相关联的邻域系统来表示.表示的过程即是建立MRF模型的过程.

2.1 邻域系统与基团

对于任意二维场景图像，我们把它分成M×N大小的宏块B.

B={(i，j)|1≤i≤M，1≤j≤N}

邻域系统可分为一阶、二阶、多阶邻域系统.本实验主要采用一阶、二阶邻域系统，如图3所示.其中符号1表示当前宏块，符号0则为当前宏块的邻域系统.

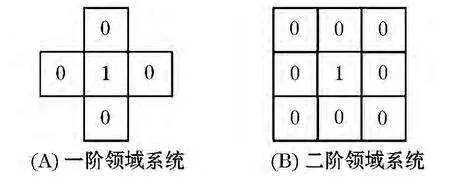
图3 一、二阶邻域系统

基团是宏块B的子集，它可以表示成单点基团、双点基团等，其数量是由邻域系统的阶数所决定的，一阶邻域系统的基团如图4所示.

图4 一阶邻域系统的基团

2.2 纹理能量

二维场景图像中，每一宏块的纹理能量值都与纹理基元有关.实验表明，纹理能量统计特性与尺度的关系如图5所示[10].当所选尺度较小时，即在a、b尺度范围内，远处所能捕捉到的纹理能量信息多于近处所能捕捉到的纹理能量信息.随着尺度的增加，远、近处所能捕捉到的纹理能量都在增加，但是，近处的纹理能量信息增加速度较快，而远处纹理信息逐渐达到最大值状态.在b、c尺度范围内，远、近处的纹理能量均达到了最大值.随着尺度的进一步增大，在c、d尺度范围内，远、近处的纹理能量信息均处于减少状态，逐渐趋近于零.

2.3 算法模型

2.3.1 深度更新开关函数

为了更好的描述多尺度纹理能量与深度信息之间的关系，本文定义了一个开关函数，称为深度更新开关函数，用此开关函数来描述不同尺度纹理能量对深度值的影响.Es表示任一宏块B在第s个尺度的纹理能量值，E*s表示该宏块在第s个尺度邻域纹理能量值的均值.本算法中对每个宏块提取了5个尺度的纹理能量，按远、近处纹理能量统计特性，如图5所示，可将开关函数分为以下三种情况:

1)若 Es≤Es+1，1≤s≤4

且E*s≤Es+1，1≤s≤4，则说明该块在 a、b 尺度区间，则:

2)若max(E*s)和max(Es)各自所在的尺度分别为s*和sE，则:

3)若 Es≥Es+1，1≤s≤4

且 Es≥Es+1，1≤s≤4，则说明该块在 c、d 尺度区间，则:

2.3.2 深度更新准则

为有效地估计深度信息，在纹理能量的基础上，不仅设计了深度更新开关函数，还设计了如式(3)所示的深度更新准则.

深度更新准则对图像深度按宏块进行更新，式中d*是该宏块的邻域深度值的均值，λ为深度更新调整幅度因子，f控制是否对深度值进行更新，图像每个宏块的深度信息从初始值d(0)开始迭代，d(n+1)是宏块经过迭代后更新的深度值.

2.3.3 深度估算迭代步骤

1)深度值初始化

每个图像宏块深度初始值d(0)的选取，影响迭代算法的收敛速度，深度初始值采用本课题前期阶段的研究结果，即将最小二乘方法得到的实验结果作为深度初始值[11－12].该最小二乘方法根据纹理特征矢量Ω与宏块真实深度d之间的关系训练参数矢量θ，参数矢量θ表示图像每一纹理对深度影响的不同权值的组合.

深度信息可由参数矢量θ与纹理特征矢量Ω按公式(5)运算获得，把公式(5)运算的结果作为本迭代算法的宏块深度初始值d(0).

2)深度更新

任一宏块深度值按照深度更新准则公式(3)来调整宏块深度值d(n)，所得d(n+1)的值作为d(n)的深度更新值.

3)迭代终止判决

迭代过程中每一宏块的深度值不断更新，整幅图像所有宏块深度信息更新结果构成整幅图像更新的深度信息.整幅图像深度信息经过更新所得到的深度图像表示为是深度更新第次所得到的深度图像中第行第列宏块的深度值.整幅图像经过每次迭代后，判断是否满足式(6)的收敛判决条件.如不满足返回步骤2继续迭代，如满足式(6)，则迭代终止.迭代终止后，获得的整幅图像深度信息，即为深度信息最终估计结果.

式(6)中的为判断深度信息调整是否达到稳定状态的阈值.

3 实验结果

为验证方法的有效性，本文选取康奈尔大学的二维场景图像及真实深度图像作为样本训练集.样本中二维场景图像包括人造环境(楼房，街道等)，自然环境(森林，灌木丛等).其中以400幅二维场景图像为训练样本集，像素是1 704×2 272，另133幅1 704×2 272的二维场景图像作为测试样本集.本实验以Matlab.2011b作为实验平台.见图6.

图6 实验结果

实验中，宏块的大小会影响实验结果，宏块过小，不仅会失去深度值的统计特性，而且会延长训练时间.宏块过大，虽然会提高训练速度，但是深度值的统计特性不明显.因此，我们把每幅图像分成像素的固定宏块.实验中，公式(3)中λ选取0.05，公式(6)中ε设定为1，实验结果如图6所示，原始图像(A)包括楼房，树木，天空等.(B)组图像是激光扫描设备得到的二维场景图像的真实深度图像.(C)组图像是本实验二维场景图像深度图.实验中的深度范围是在0～81 m，对于深度远于81 m的深度都记为81 m.

4 结语

在本方法中，提出了一种基于MRF模型与多尺度纹理特征的单幅图像深度信息估计方法.采用Laws滤波器对二维场景图像提取多尺度纹理能量信息，根据纹理能量信息的统计特性构建MRF，通过迭代算法获得二维场景图像的深度信息.

实验结果证明，本方法对于纹理轮廓明显或者图像中深度差异较大的二维场景图像，能够得到较好的实验结果.但是，对于纹理轮廓不明显或者图像中深度差异较小的二维场景图像，效果并不理想.在未来的研究中，可以针对这个问题，在提取深度特征方面，尝试提取其他特征，或者针对不同的特征按不同权值采用融合策略进行分配，以提高深度信息估计效果.

[1]KARSCH K，LIU C，KAN S B.Depth Extraction from Video U-sing Non－parametric Sampling[C]//European Conference on Computer Vision，2012.

[2]CHAOCHUNG C，CHENGTE L，POSUN H.A block－based 2D－to－3D conversion system with bilateral Filte[C]//International Consumer Electronics，Las Vegas，NV，USE，2009:1－4.

[3]张蓓蕾，孙韶媛.基于马尔科夫场理论的单目图像深度估计[D].上海:东华大学，2010.

[4]KNORR S，IMRE E.OZKALAYCI B，et al.A modular scheme for 2D/3D conversion of TV broadcast[C]//3D Data Processing，Visualizati，and Transmission，Third International Symposium，2006:703－710.

[5]MALIK J，ROSENHOLTZ R.Computing local surface orientation and shape from texture for curved surface[J].Intermation Journal of Computer Vision，1997，23(2):149－168.

[6]SAXENA A，SCHULTE J，ANDREW Y N.Learning 3－D scene structure from a single still image[C]//IEEE Tractions on PAMI，2009:824 －840.

[7]SAXENA A，SCHULTE J，ANDREW Y N.－MRF:capturing spatial and semantic structure in the parameters for scene understanding[C]//Neural Information Processing Systems Conference 2011.

[8]谢世明，胡茂林.纹理的特征提取与分类研究[D].合肥:安徽大学，2006.

[9]葛 亮，朱庆生，傅思思.Laws纹理模板在立体匹配中的应用[J].光学学报，2009，29(9):2507－2508.

[10]蓝建梁，丁友东，黄东晋.基于多尺度纹理能量测度的单幅图像深度估计[J].计算机工程与设计，2011，32(1):224－227，231.

[11]ZHANG L Z，CHEN T T.The image depth estimation based on multi－scale texture features and least－square method[C]//International Conference on Signal Processing，2012.

[12]周庆欣，吴玉东，范红霞，等.加权Markov链权重计算及应用[J].哈尔滨商业大学学报:自然科学版，2014，30(6):740－743.