聚类算法在数据挖掘领域的研究
蔡程宇,娄渊胜
(河海大学,南京210000)
聚类分析[1-5]的重要性及涉及各个领域的研究已经深入人心.而聚类算法的研究在各个领域已经被广泛应用并且不断的提高,它也是数据挖掘[6]技术的最重要组成部分,能将隐藏在底层的未知的数据得以被发现,目前已经广泛应用于模式识别中的一些图像处理[7-8],数据分析等其他领域的许多方面.因此它的重要特征是在某一类中,所有的对象在一定程度上有相似点,同类数据之间的相似性越小越好,不同类数据之间的相似性越大越好.
1 聚类
1.1 聚类概念
这里给出关于聚类所下的定义:一个簇内的实体应该是尽可能的相似,而不同簇内的实体应该是尽可能的不相似;在同一个类内,空间中的数据对象的汇集是通过距离测量得到的,在同一类内的任意两个点间的距离必须要小于不同类簇的任意两个点间的距离;类是一个密度较高的点的集合的多维空间而形成的一个连通区域[9-11],通过相对密度较低的点集来区分不同的类.
设给定一个输入模式的集合Z={X1,X2,X3…,Xn},Xi表示集合 Z 中的第i个模式 i={1,2,3…,n};因此我们要把n个模式硬划分为K类,即C={C1,C2…,Ck}(K≤N),这 K 个划分满足一下几个条件:
1)Ci≠φ,i=1,2,…K
2)∪ki=1Ci=Z 且对∀ci,cj⊆z ci∩cj= φ,ci≠cj,i,j=1,2…K 且 i≠j
1.2 聚类准则
1.2.1 离差平方和准则(最小方差分割)
假设n个样本分成了K类,Xj∈Z对i=1,2,…k和 j=1,2,…n,定义如下;mij=1,表示第i类中含有第j个样本则mij标注为1
令ni表示第i类中所包含的样本个数,
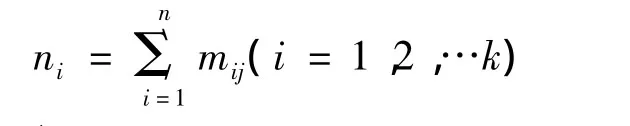
设Pi∈z表示第i类的中心,则


1.2.2 离散度准则
第1类内离散度矩阵,首先得到第i类的离散度矩阵,假设mi是第i类的中心,则第i类中所有样本相对该类中心的离散程度为:
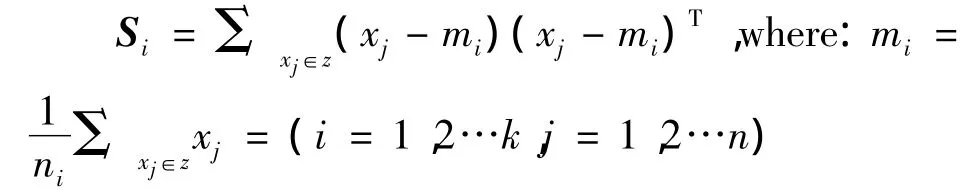
则总的内离散度矩阵的和为:
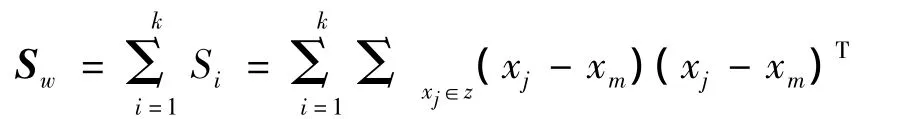
第2类间离散度矩阵,每一类的中心相对总的中心的离散程度和为:
SB,m 是所有样本中心第3总离散度矩阵,所有样本相对总的中心的离散程度:-m)]T=↑SB+SW.ST在这里面是不变量,即为常数,SB,SW随样本划分的改变而改变,因此与样本划分有关,而SB,SW,都是矩阵,通过定准则比大小.
若k=n,则一个点成一个类,那么这样的聚类显然是没有意义的,且离差平方和准则达到最大,所以系数k的确立是对整个离差平方和准则有着重大影响并对J的影响也不容忽视.
2 传统聚类算法分类图
见图1.

图1 聚类算法分类
3 聚类算法比较分析
3.1 基于划分的聚类算法
3.1.1 k-means算法
k-means是聚类算法中最简单的一种了,但是它的算法思想却非比寻常,在聚类问题中,我们可以假设样本{x(1),x(2),x(3),…x(n)}∈Z,k -means算法是将n个样本聚类成k个簇,具体算法描述:
1)随机选取 k 个聚类质点为 v1,v2,v3…,vk∈Z.
2)Repeat{
对于每一个样例i,计算其应该属于的类
c(i):=argmin‖x(i)-vj‖2
对于每一个类j,重新计算类的质心

}直到收敛为止,算法结束
k是一个常量,c(i)代表第i个数据对象与k个类中质点距离最近的值,质心vj代表同一个类的样本中心.
3.1.2 PAM、CLARANS 算法
在PAM算法中假设非代表对象Oh替换当前代表对象Oi的总代价为Uih,非代表对象Oh替换当前代表对象Oi所产生的对于非代表对象Oj的代价为Ujih.则对每个非代表对象Oi,计算Ujih有以下四种情况:
1)Oj∈Oi,对任意代表数据对象 Om,若 Oi被Oh替换,d(Oj,Om)min,则 Oj∈Om,Ujih=d(Oj,Om)- d(Oj,Oi).
2)Oj∈Oi,对任意代表数据对象 Om,若 Oi被Oh替换,d(Oj,Oh)min,则 Oj∈Oh,Ujih=d(Oj,Oh)- d(Oj,Oi).
3)Oj∈Om,对任意代表数据对象 Om,若 Oi被Oh替换,d(Oj,Om)min,则,Oj∈Om,Ujih=0.
4)Oj∈Om,对任意代表数据对象Om,若Oi被Oh替换,d(Oj,Oh)min,则 Oj∈Oh,Ujih=d(Oj,Oh)- d(Oj,Om).
因此Uth=Σijih为Oi替换对所有的非代表对象Oj的总代价.如果Uih<0则Oh替换Oi,进入循环迭代操作,否则质心不变.
在CLARANS算法中首先假设几个参数:numlocal和maxneighbor分别表示抽样次数和任意一个节点与邻居节点比较数目,i用来表示已选样的次数,mincost为最小代价,current为当前节点,j表示已经与当前节点进行比较的邻居个数.PAM和CLARANS的算法流程图见图2、3.
3.2 基于层次的聚类算法
BIRCH在层次聚类算法中属于至关重要的算法之一,即平衡迭代削减聚类.其中涉及到聚类特征(CF)和聚类特征树(CF Tree)两个概念,主要思想是通过扫描数据库,建立一个初始存放于内存中的聚类特征树,然后对聚类特征树的叶结点进行聚类.它的核心是聚CF和CF Tree.CF是指三元组CF=(N,LS,SS),用来概括子簇信息.其中:N为簇中d维点的数目;LS为N个点的线性和;SS为N个点的平方和.CF树是一棵具有两个参数的高度平衡树,用来存储层次聚类的聚类特征.它涉及到两个参数分支因子和阈值.CF树的构造过程实际上是一个数据点的插入过程,其步骤见图4.
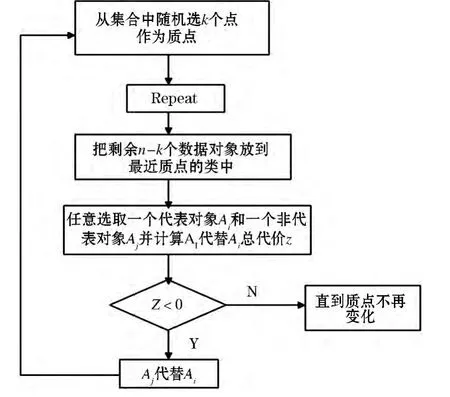
图2 PAM算法流程
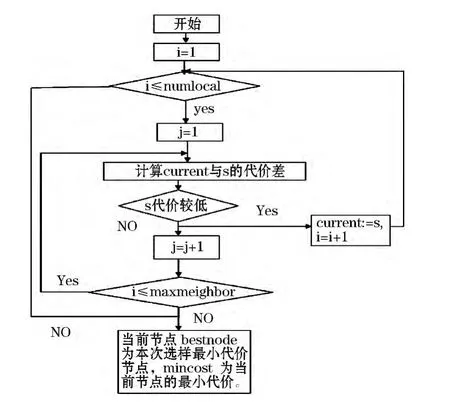
图3 CLARANS算法流程

图4 BIRCH算法流程
3.3 基于密度的聚类算法
DBSCAN算法是基于密度的聚类算法,它有着显著的不同,它是将高密度的点相互连接起来的一个最大集合并能快速找到不规则形状的聚类.
DBSCAN算法描述:
在DBSCAN算法中要设法找到一个类,首先要假设两个参数,eps及MinPts分别代表半径和最小数目,然后从数据库中随机取得一个数据对象Z,并计算与该对象Z以半径eps为阈值范围的所有对象的个数,如果个数大于等于MinPts,则对象Z为核心对象,即可找到关于这两个参数的一个类.如果对象Z为一个临界点,即不满足MinPts,因此Z对象被标记为噪声点,依次循环处理下一个未被标记的数据对象来对聚类进行拓扑.见图5.
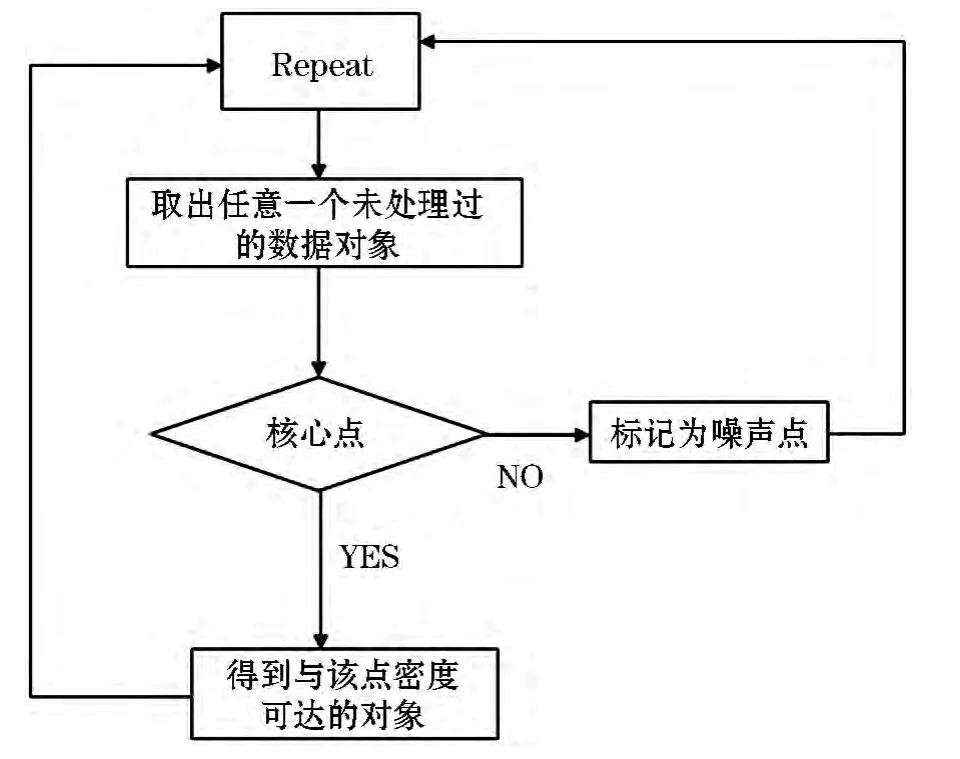
图5 DBSCAN算法算法描述
上述DBSCAN流程图中所定义到的eps及MinPts参数对整个结果影响是非常大的,而对于用户的选择来说是随机不定的,因此这也是我们应该要解决的问题.
计算与对象Z以半径eps为阈值范围的所有对象个数的过程需要不断执行区域查询来实现,并把查询的结果反馈回来,这种有效的查询是通过使用空间查询R-树结构,首先,必须建立R*树,第二步,对于参数的选择,在这里又引入了k-dist图,是计算所有对象与它的第k个最近的对象之间的距离,对计算的结果进行从小到大的排序并绘k-dist图.横坐标表示任意对象与第k个最近数据对象之间的距离,而纵坐标表示相同距离值的数据对象的个数.虽然工序复杂,但是k-dist图可以为eps取值带来很好的效果.
3.4 基于密度和网格的聚类算法
CLIQUE算法是基于密度同时基于网格的聚类算法.主要用于找出在高维数据空间中存在的低维聚类,采用了子空间的概念来进行聚类,因此它适合处理解决高维数据.CLIQUE聚类算法空间划分和密集单元:
设 A={C1,C2,C3,……,Cn}是个有界的定义子空间,则S=C1×C2×C3×……×Cn就是一个n维的数据空间,将 C1,C2,C3,……,Cn看作 S 的属性或者字段.
clique算法的输入对象是一个n维空间中的数据对象点集,设为 u={u1,u2,u3,……,un},其中 ui={ui1,ui2,ui3,……,uin},ui的第个 j分量 uij∈Cj.
算法中,输入一个参数a,可以将空间S的每一维分成相同的a个区间,从而将整个空间分成有限(an)个互不相交的矩形单元格,每一个这样的矩形单元格可以描述为{v1,v2,……,vn},其中vi=[li,hi),均为一个前闭后开的区间.
通常说一个数据对象 u={u1,u2,u3,……,un}落入一个单元格v={v1,v2,……,vn}当且仅当对于每一个vi都有li≤ ui<hi成立.
一个单元的选择率s(v)为s(v)=单元格中的点数/总的点数,设定一个密度阈值w,称数据单元u是稠密的,当s(v)>w.
Clique利用的一个性质:如果一个k维单元是密集的,那么他在k-1维空间上的投影也是密集的.也就是说,给定一个k维的候选密集单元,如果检查它的k-1维投影单元,发现任何一个不是密集的,那么就知道第k维的单元也不可能是密集的.因此可以从k-1维空间中发现的密集单元来推测k维空间中潜在的或候选的密集单元.(类似于Aprior性质)
4 聚类算法性能比较
见表1.
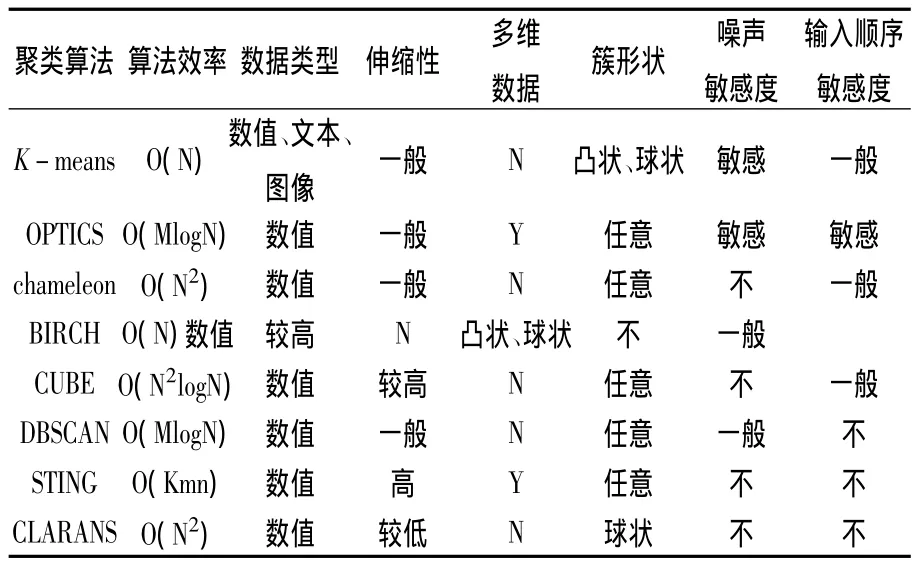
表1 多种算法的性能比较
5 结语
聚类算法目前仍然是数据挖掘领域的一个热点,并且在好多领域得到广泛的应用,如:机器学习,模式识别,天文物理等各个研究领域,在本文中也例出了几个经典的聚类算法,并对其思想,性能和优缺点进行了深度分析,因此聚类不仅是过去,现在,乃至将来都是一个具有不可取代地位的一门学科.
[1]JAIN A K,DUIN R P W,MAO J C.Statistical pattern recogni-tion:A review.Pattern Analysis and Machine Intelligence,IEEE Transactions on,2000,22(1):4-37.
[2]李明华.数据挖掘中聚类算法的新发展[D].苏州:苏州大学计算机科学与技术学院,2008.
[3]朱 强.粒度计算在聚类分析中的应用[D].合肥:安徽大学,2007.
[4]张建华,江 贺,张宪超.蚁群聚类算法综述[D].阜阳:大连理工大学软件学院,2006.
[5]HAN J,KAMBER M.Data Mining:Concepts and Techniques[M].San Francisco:Morgan Kaufmann,2006.
[6]韩彦芳,施鹏飞.基于蚁群算法的图像分割方法[J].计算机工程与用,2004,40(18):5-7.
[7]HAN J W,KAMBER M.数据挖掘概念与技术[M].北京:机械工业出版社,2001.
[8]郭 里.并行层次聚类技术研究[D].长沙:湖南大学,2007.
[9]杨彦侃.并行的聚类算法研究[D].包头:内蒙古科技大学,2010.
[10]钱彦江.大规模数据聚类技术与实现[D].成都:成都电子科技大学,2009.
[11]周庆欣,吴玉东,范红霞,等.加权Markov链权重计算及其应用[J].哈尔滨商业大学学报:自然科学版,2014,30(6):740-743.

