“数据的收集、整理和描述”典例解读

钟雁平

《数据的收集、整理、描述》这一章整个初中数学统计知识的基础，所以各地中考关于这章内容的命题基本都依托日常生活背景，利用统计图表呈现数据，来考查同学们的读图作图能力、数据处理能力.下面根据本章的知识点列举了一些典型的中考题.

一、简单的读图和计算

例1（2014年江苏扬州）如图，某校根据学生上学方式的一次抽样调查结果，绘制出一个未完成的扇形统计图，若该校共有学生700人，则根据此估计步行的人有________人.

【考点】用样本估计总体；扇形统计图.

【分析】先求出步行的学生所占的百分比，再用学生总数乘以步行学生所占的百分比即可估计全校步行上学的学生人数.

【点评】本题考查了扇形统计图及用样本估计总数的知识，解题的关键是从统计图中得出步行上学学生所占的百分比.

例2 （2014年江苏无锡）为了解“数学思想作文对学习数学帮助有多大？”一研究员随机抽取一定数量的高校大一学生进行了问卷调查，并将调查得到的数据用下面的扇形图和表来表示（图、表都没制作完成）.根据图、表提供的信息.

【点评】本题考查的是扇形统计图的综合运用.读懂统计图，从统计图中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.

例3（2014年江苏苏州）某学校计划开设A，B，C，D四门校本课程供全体学生选修，规定每人必须并且只能选修其中一门.为了了解各门课程的选修人数，现从全体学牛中随机抽取了部分学生进行调查，并把调查结果绘制成如图所示的条形统计图.已知该校全体学生人数为1200名，由此可以估计选修C课程的学生有 人.

【考点】1.条形统计图；2.频数、频率和总量的关系；3.用样本估计总体.

【分析】根据样本的数据，可得样本C占样本的比例，根据样本的比例，可C占总体的比例，根据总人数乘以C占得比例，可得答案.

【点评】本题考查了用样本估计总体，先求出样本所占的比例，估计总体中所占的比例.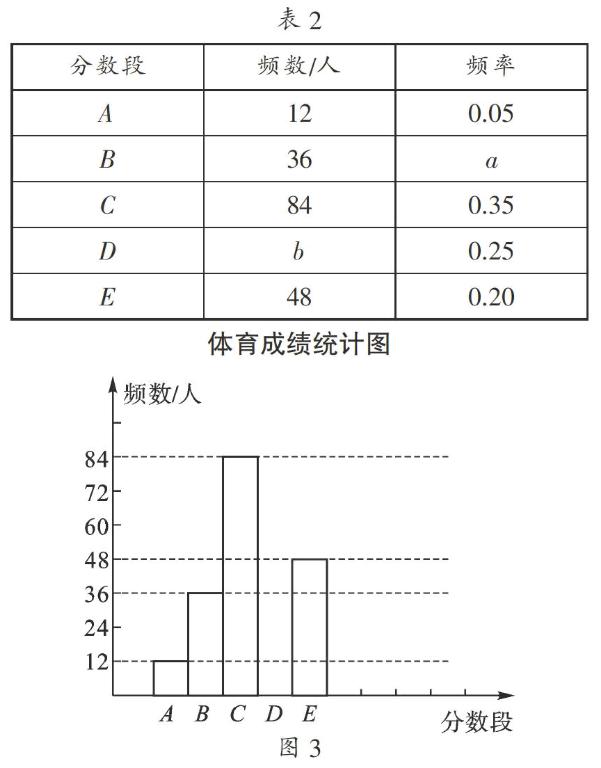

例3 （2014年江苏无锡）为了解“数学思想作文对学习数学帮助有多大？”一研究员随机抽取一定数量的高校大一学生进行了问卷调查，并将调查得到的数据用下面的扇形图和表来表示（图、表都没制作完成）.根据图、表提供的信息.

【考点】频数（率）分布直方图；用样本估计总体；频数（率）分布表；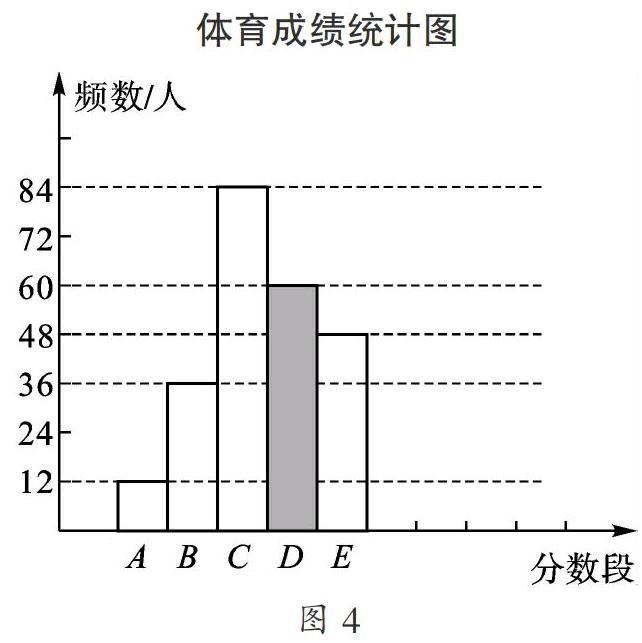

【分析】（1）首先用12÷0.05即可得到抽取的部分学生的总人数，然后用36除以总人数得到a，用总人数乘以0.25即可求出b；根据表格的信息就可以补全频数分布直方图；（2）利用48000乘以抽查人数中优秀的学生人数所占的频率即可.

即该市今年48000名初三年级学生中体育成绩为优秀的学生人数约有21600人.

【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题.同时考查了用样本估计总体的思想.

【考点】频数（率）分布表；用样本估计总体；扇形统计图.

【分析】根据B类频数和频率求出总数，再进行计算即可.

【解答】 解：（1）问卷调查的总人数是： =100（名）a= =0.3，b=100×0.06=6（名），

（2）类别为B的学生数所对应的扇形圆心角的度数是：360°×0.4=144°；

（3）根据题意得：1000×0.24=240（名）.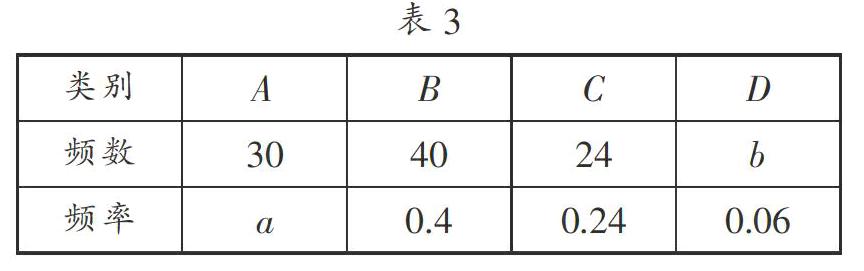

【点评】此题考查了扇形统计图和频数（率）分布表，关键是正确从扇形统计图和表中得到所用的信息.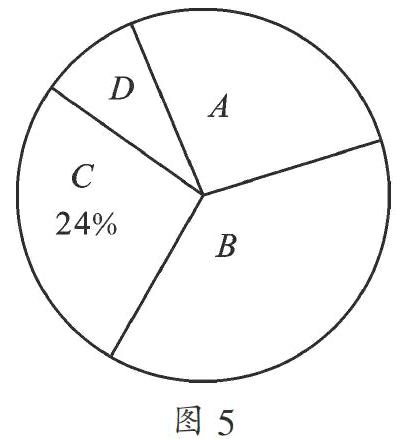

统计图表是整理、呈现数据的重要工具，所以很多考题都涉及到一种或两种统计图表，尤其以扇形统计图、条形统计图、频数分布直方图居多，另外很多还会综合考查平均数、概率等后续相关内容.本文列举的只是中考题的一部分，但做这类题目最重要的还是要把概念理解透彻、学会读懂图表，利用好图表工具.