粘性双调和Camassa－Holm方程整体弱解的存在性与唯一性

甘在会

(天津大学 应用数学中心，天津 300072)

0 引 言

1993年，Camassa 等［1］在浅水波方程的研究中导出了一类粘性Camassa－Holm 方程，

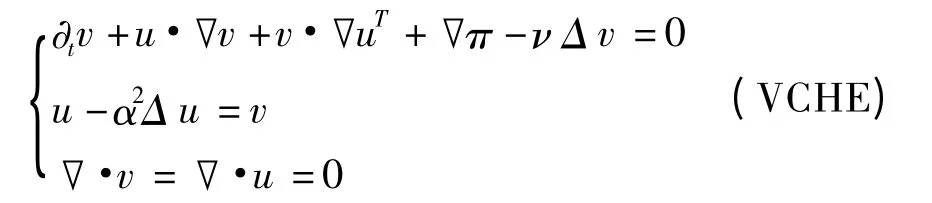
其中，α 是一个非零实常数，ν ＞0 为粘性系数，π 是压力.方程组(VCHE)也可通过变分原理和拉格朗日平均来导出［2－10］，且(VCHE)也可称为Navier－Stokes－α方程组［6］.本研究将在系统(VCHE)的基础上，考虑n维空间中的一类粘性双调和Camassa－Holm 方程(Navier－Stokes－α－β 方程组)，

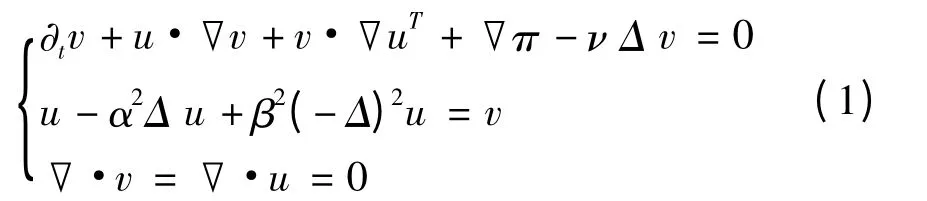
关于粘性Camassa－Holm 方程(VCHE)，科研人员已经取得一些成果［2－5，8，10］.在此基础上，本研究将讨论n 维粘性双调和Camassa－Holm 方程(1)整体弱解的存在性与唯一性，其中，n = 2，3.

先给出一些记号:Lp表示标准勒贝格空间，其范数表示为，，＜u，v ＞=uvdx，表示在Hilbert 空间L2上的标准内积.令，，则表示∑在范数‖·‖p下的完备化空间，Wm，p表示标准的Sobolev 空间，且Hm= Wm，2表示∑在Hm范数下的完备化空间，)' 表示的对偶空间，或表示函数ø 的Fourier 变换，ø或(ø)表示函数ø 的Fourier 逆变换.

1 预备知识

赋予粘性双调和Camassa－Holm 方程(1)如下初值，

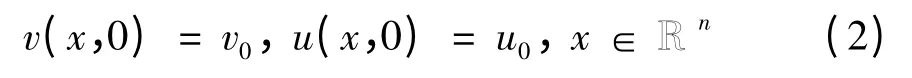
于是可得，

引理1 令u 和v 是具有紧支集的光滑函数，n= 2，3，且·u =·v = 0，则如下式子成立，

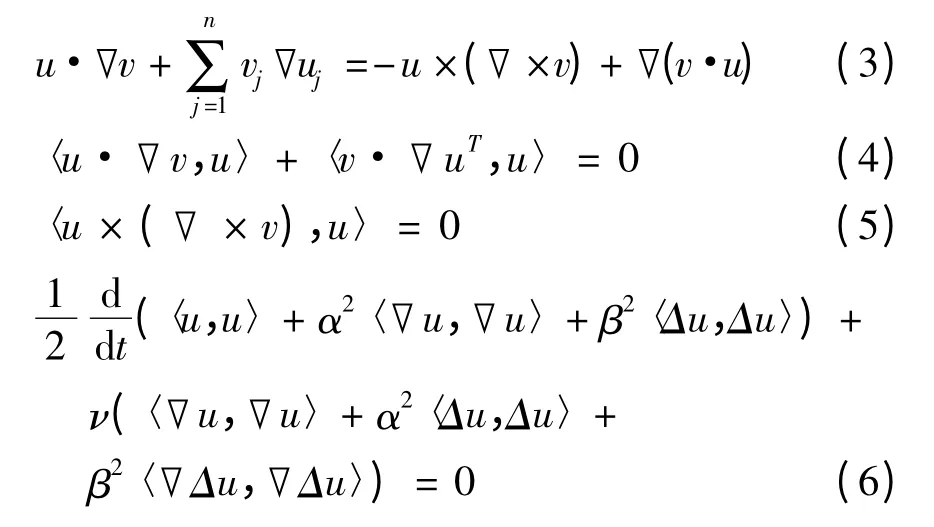
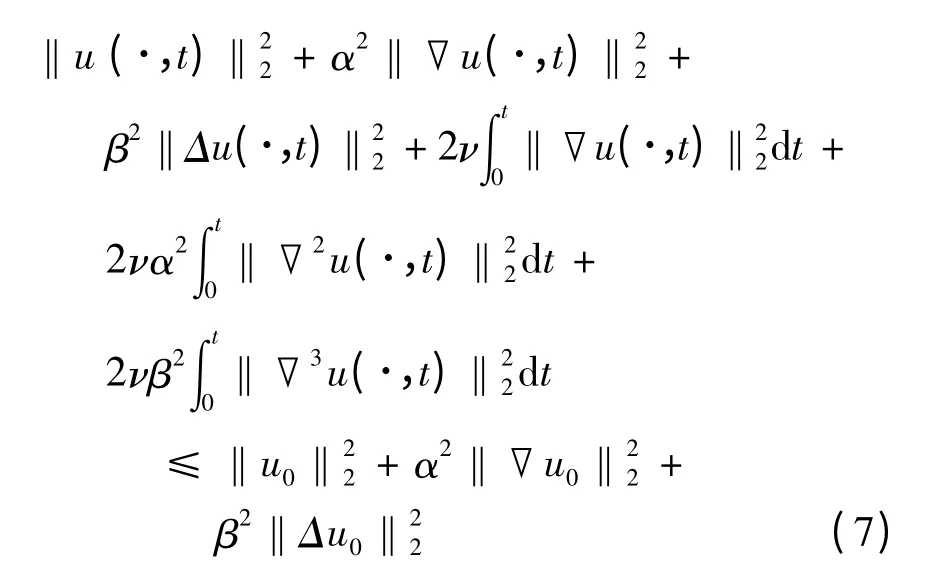
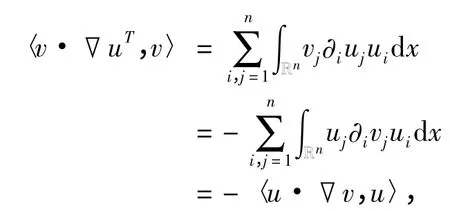
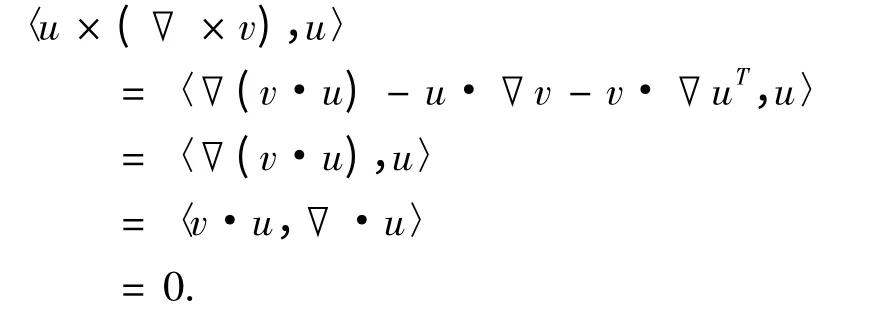
在式(1)中第一式两端与u 作内积得，

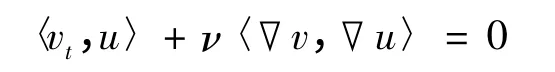
再利用式(1)中第二式可得，

即式(6)成立.关于t 积分式(6)两端知，式(7)成立.

对于粘性双调和Camassa－Holm 方程(1)，给出如下2 个关于弱解的定义.

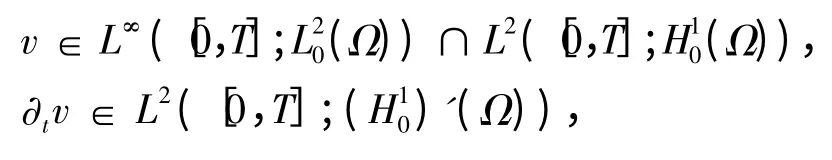
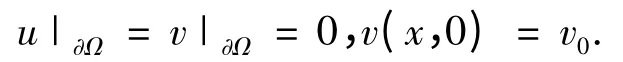
此外，对任意ø ∈L2(［0，T］;(Ω))，且ø(T)= 0，如下等式成立，

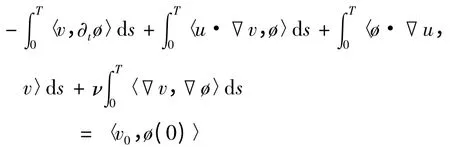
且关于t 几乎处处成立，

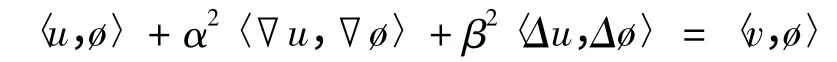
此外，对任意ø ∈L2(［0，T］;，且ø(T)= 0，如下等式成立，

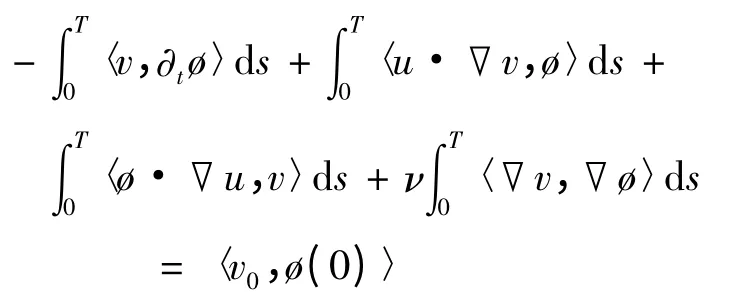
且关于t 几乎处处成立，

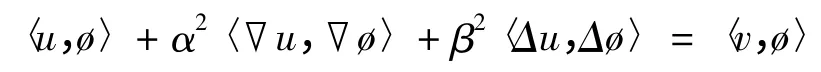
2 主要结果及先验估计式

本研究的主要结果即粘性双调和Camassa－Holm 方程(1)在定义1 及定义2 意义下整体弱解的存在性与唯一性.

定理1 给定初值v0∈(Ω)，其中，Ω ⊂n是具有光滑边界的开有界集，且v0|=0，或者Ω =n，n = 2，3，M ≥0=.则 粘 性 双 调 和Camassa－Holm 方程(1)在定义1 或者定义2 意义下存在唯一的整体弱解.此外，这个弱解满足估计式(7)，且对所有m +2k ≤M 时，如下估计式成立，

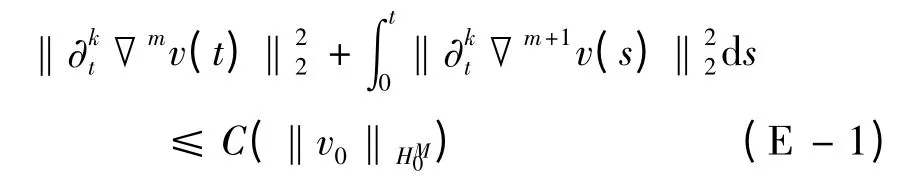
为了证明定理1，首先给出几个重要的引理.

引理2 给定v ∈Lp(n)，p ∈(1，∞)，n = 2，3，双调和Helmholtz 方程，

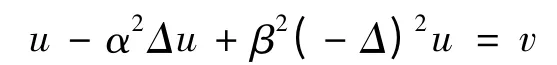
存在一个弱解，u ∈W2，p(n).此外，函数u 和v 满足如下估计式，

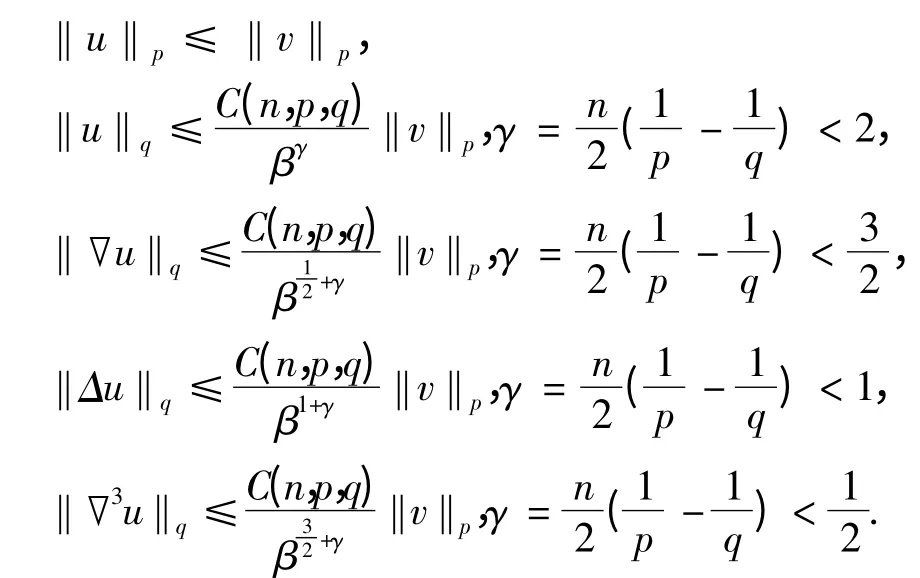
证明 利用椭圆估计、Sobolev 嵌入定理及插值估计，可得到引理2 的结论.

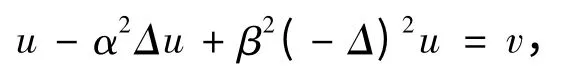
则，

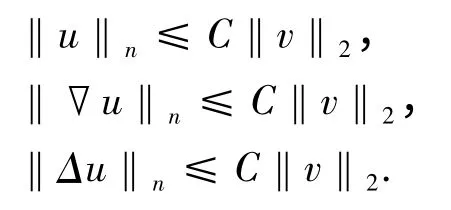
其中，常数C 仅依赖于α，β，Ω 及n.

证明 利用Poincaré 不等式及Gagliardo－Nirenberg－Sobolev 不等式可推得该引理中的估计式.

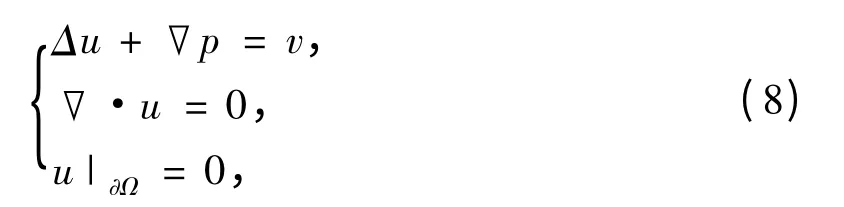
及，

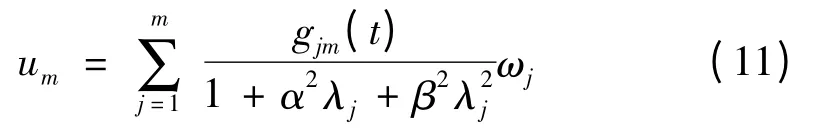
此外，近似解式(10)、(11)满足如下关系式，

证明 将式(10)、(11)代入方程(1)，并与ωi作内积得，

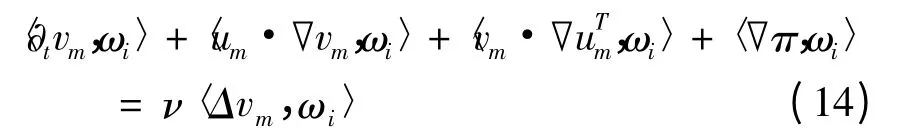
此式代入式(14)可推知，近似解式(10)、(11)满足关系式(12).注意到Pm∶L20(Ω)→Hm，由式(10)知vm(0)= Pmv0，即式(13)成立.

将式(10)、(11)代入式(12)可得，

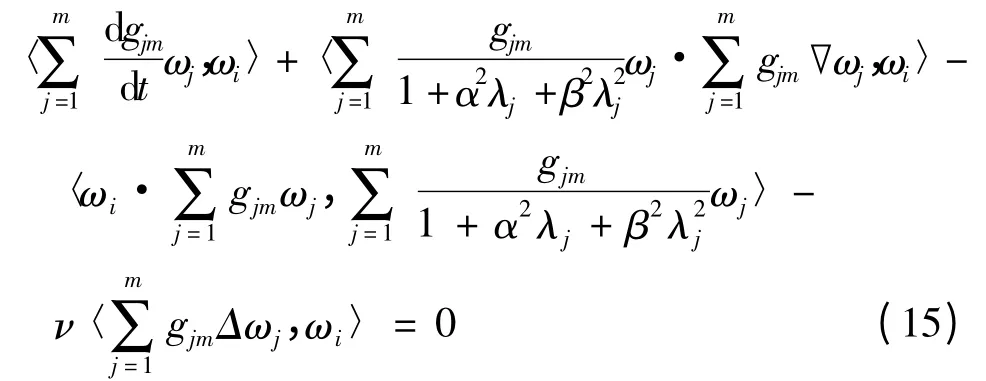
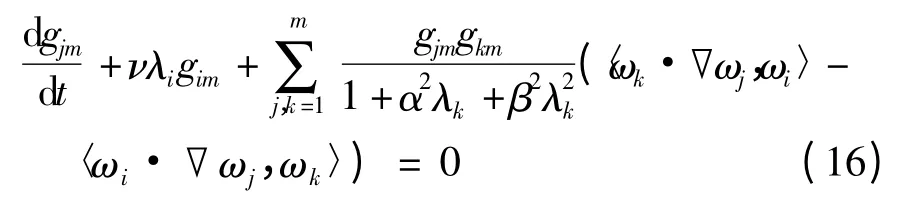
方程(16)是关于gim的一个m 阶常微分方程系统.由常微分方程解的局部存在性理论知，在某一时间区间［0，Tm］上，方程(16)的解gim有定义且存在.

下面的引理5 给出了Tm一致有界(不依赖于m)，即对任意m，Tm= ∞.

引理5 令n = 2，3，由引理4 构造的近似解满足如下估计式，

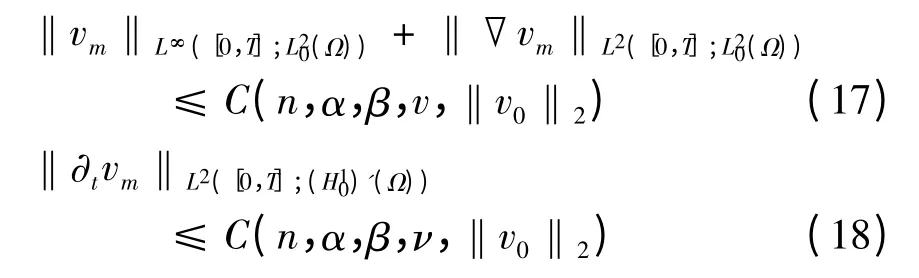
其中，C = C(n，α，β，ν，‖v0‖2)不依赖于T，Ω及m.

证明 在式(12)两端同乘，

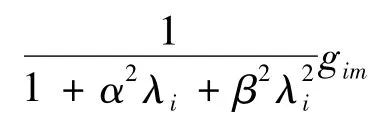
并求和知，

利用式(11)，及um－ α2Δum+ β2(－ Δ)2um=vm，式(19)蕴含着，

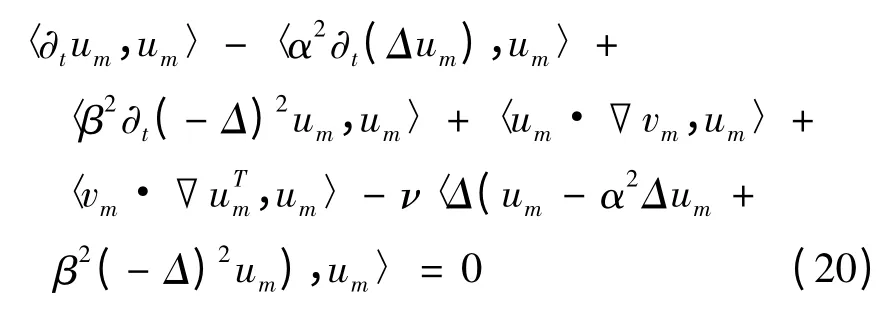
由引理1 知，〈um·vm，um〉+〈vm·，um〉= 0.于是，由式(20)可推导出，

即，

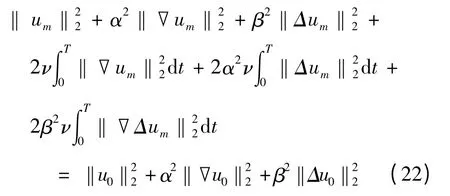
于是，式(17)成立.此外，由，

可知，

根据式(17)，将引理3 应用到近似解vm，um知如下估计式成立，

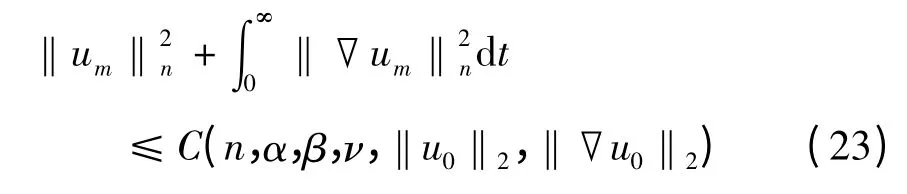
因对任意ø ∈H20(Ω)可用ωi求和来表示，故由式(12)知每个近似解满足，

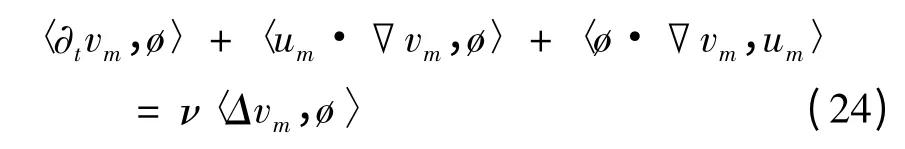
利用分部积分，Hölder 不等式及Gagliardo－Nirenberg－Sobolev 不等式可推得，

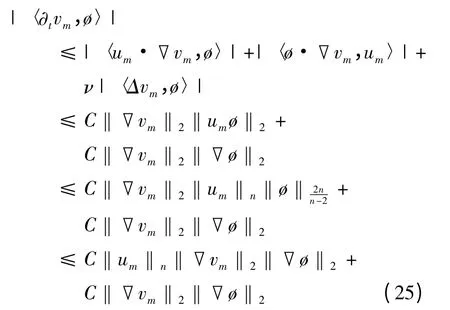
由此可得，

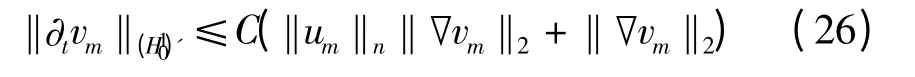
结合式(13)、(22)、(23)与(26)知，

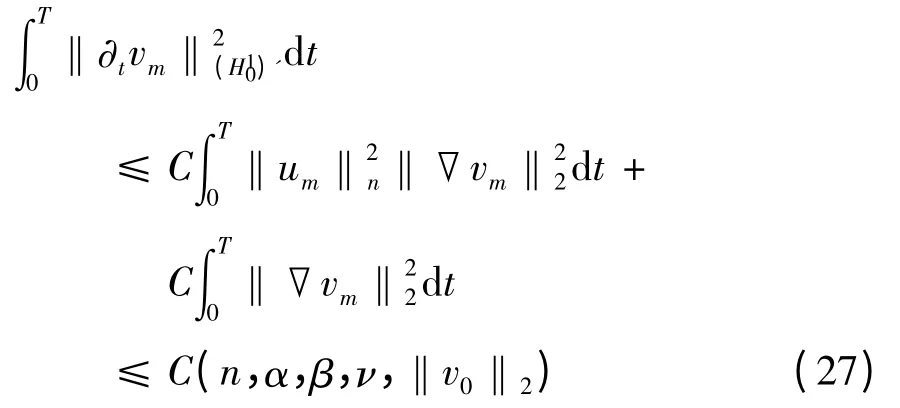
即式(18)成立.

3 主要结果证明(定理1 的证明)

定理1 的证明

1)证明在定义1 意义下Camassa－Holm 方程(1)弱解的存在性，即如下结论成立.

证明 注意到引理4 及引理5，这里仅需证明近似解的收敛性.引理5 蕴含着序列vm有界，根据Banach－Alaoglu 定理，可抽取vm的一个子序列(为了方便，仍用vm表示)满足存在一个函数v，

使得，

在L∞(［0，T］(Ω))中，vm弱*收敛于v (28)

在L2(［0，T］;(Ω))中，vm弱收敛于v.(29)

下面证明，v 是方程(1)的一个弱解，根据引理4中近似解的构造，对任意基矢量ωj∈L20(Ω)及任意光滑标量关于时间的函数øj(t)使得，øj(T)= 0，利用分部积分知，

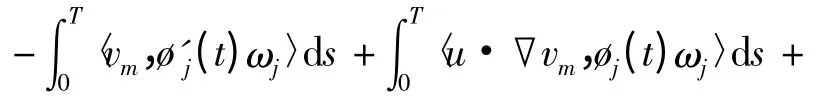
收敛性式(28)、(29)蕴含着，

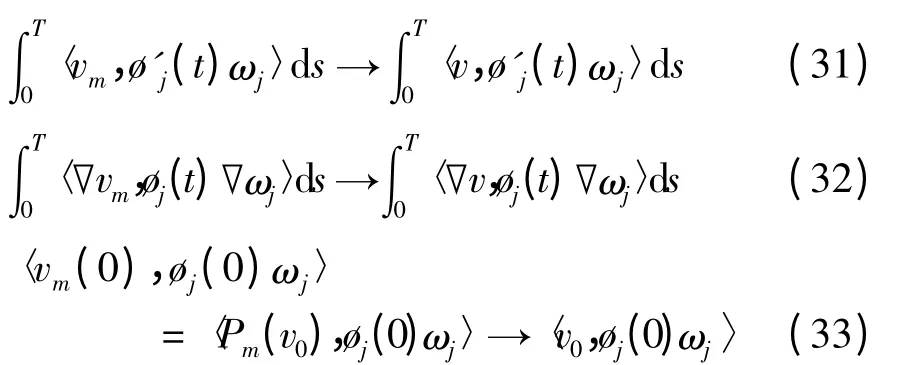
由式(17)及(18)知，存在一个子序列vm使得，

在L2(［0，T］;L20(Ω))中，vm强收敛于v (34)

注意到引理2，存在一个函数u 满足，u－α2Δu +β2(－ Δ)2u = v.于是，由引理4 可以推导出，

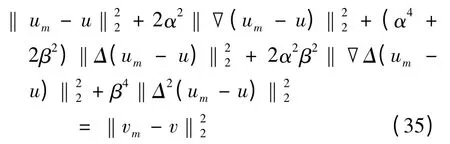
利用Gagliardo－Nirenberg－Sobolev 不等式知，

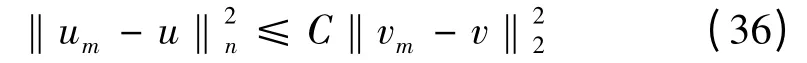
联合式(34)、(35)及(36)，利用Hölder 不等式及Gagliardo－Nirenberg－Sobolev 不等式得到收敛性估计，

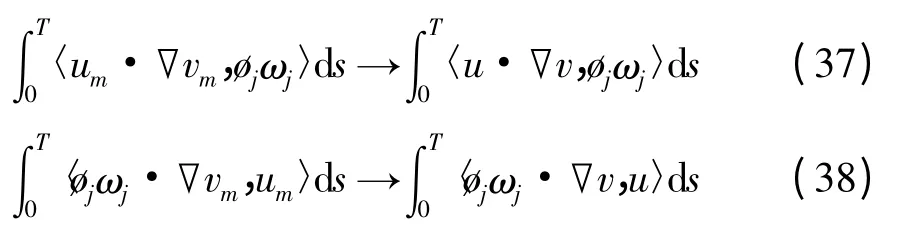
因ωj在中稠密，且øj是任意光滑函数，故由式(30)、(31)、(32)、(33)、(37)及(38)可得v 是式(1)的一个弱解.命题1 得证.

注记2 命题1 的结论在v0∈(Ω)时也成立.

2)证明在定义2 意义下Camassa－Holm 方程(1)弱解的存在性，即如下命题2 成立.

命题2 令v0∈n)(n = 2，3)，则Camassa－Holm 方程(1)在定义2 意义下存在一个弱解.

证明 设Ri是一个趋于∞的序列，在半径为Ri－ ε 的球内，χRi= 1;在半径为Ri的球的边界上，χRi= 0.由注记2 知，在半径为Ri的球上，式(1)存在一个弱解vRi，且初值为v0χRi.令vRi在半径为Ri的球外为0，可将vRi延拓到整个空间n.因式(17)、(18)不依赖于Ω，故式(17)、(18)不依赖于Ri.由Banach－Alaoglu 定理知，存在函数v，

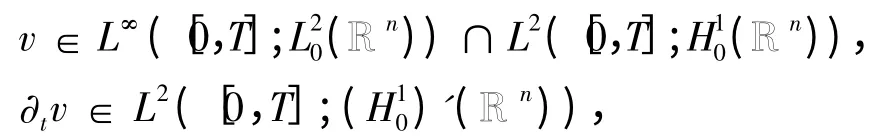
使得，

在L∞(［0，T］，vRi弱*收敛于v.(39)

在L2(［0，T］中，vRi弱收敛于v.(40)

注意到空间L2(［0，T］;H10(Rn))中存在一组正交基{øi}，其中øi光滑且关于空间具有紧支集.由命题1 及注记2，对充分大的Ri成立，

于是，可对线性项取极限Ri→∞.此外，在每个基函数øi的支集内，由强收敛性，可对非线性项取极限.最后，通过对角化讨论可证，当Ri→∞时式(41)的收敛性.于是可知，v 是粘性双调和Camassa－Holm 方程(1)在定义2 意义下的一个弱解.

3)证明正则性估计式(E－1)成立.

命题3 对于命题1，命题2 中构造的Camassa－Holm 方程(1)的弱解v，且v0∈HK0，当M +2P ≤K 时，如下正则性估计式成立，

证明 运用归纳法，由牛顿莱布尼兹公式及Gagliardo－Nirenberg－Sobolev 不等式可得到此命题中的正则性估计式成立.

4)证明在命题1、命题2 中构造的粘性双调和Camassa－Holm 方程(1)的弱解的唯一性，即如下结论成立.

命题4 在命题1、命题2 中构造的粘性双调和方程(1)的弱解是唯一的.

证明 令(v，u)和(w，q)是粘性双调和Camassa－Holm 方程(1)具有相同初值的2 个解.于是，(v－ w，u－ q)满足，

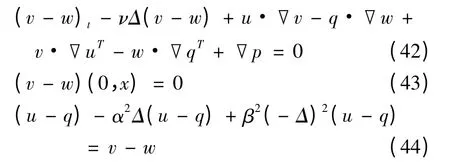
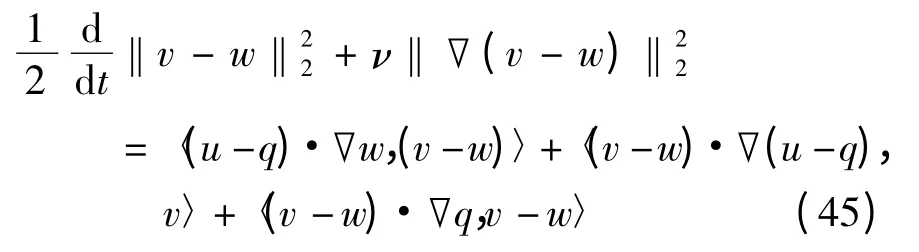
利用Hölder 不等式、Gagliardo－Nirenberg－Sobolev不等式、柯西不等式及引理3，式(45)右端项满足如下估计式，

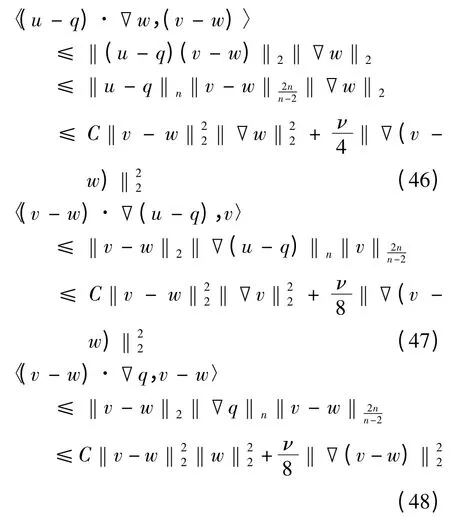
于是，由引理5 可得，

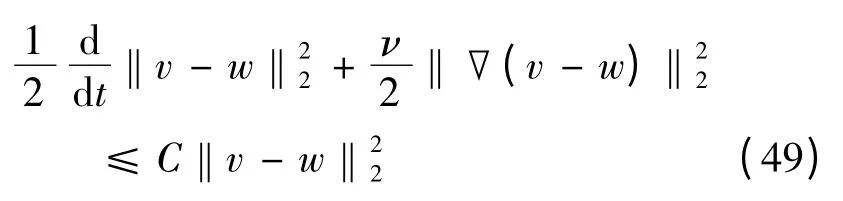
由Gronwall 不等式及‖v0－w0‖2= 0 可推知，对任意t ∈［0，T］，‖v－ w‖2= 0.

由命题1、注记2、命题2、命题3 及命题4 知，定理1 得证.

［1］Camassa R，Holm D D.An integrable shallow water equation with peaked solitons［J］.Phys Rev Lett，1993，71(11):1661－1664.

［2］Chen S，Foias C，Holm D D，et al.Camassa－Holm equations as a closure model for turbulent channel and pipe flow［J］.Phys Rev Lett，1998，81(24):5338－5341.

［3］Chen S，Foias D，Holm D D，et al.The Camassa－Holm equations and turbulence［J］.Phys D，1999，133(1－4):49－65.

［4］Chen S，Foias C，Holm D D，et al.A connection between the Camassa－Holm equations and turbulent flows in channels and pipes［J］.Phys Fluids，1999，11(8):2343－2353.

［5］Domaradzki J A，Holm D D.Navier－Stokes－alpha models:Les equations with nonlinear dispersion［EB/OL］.［2001－03－23］.http://arxiv.org/abs/nlin/013036.

［6］Foias C，Holm D D，Titi E S.The Navier－Stokes－alpha model of fluid turbulence［J］.Phys D，2001，152/153(1):505－519.

［7］Foias C，Holm D D，Titi E S.The three dimensional viscous Camassa－Holm equations，and their relation to the Navier－Stokes equations and turbulence theory［J］.J Dynam Differential Equations，2002，14(1):1－35.

［8］Ilyin A A，Titi E S.Attractors for the two－dimensional Navier－Stokes－α model:an α－dependence study［J］.J Dynam Differential Equations，2003，15(4):751－778.

［9］Holm D D，Marsden J E，Ratiu T S.The Euler－Poincar'e equations and semidirect products with applications to continuum theories［J］.Adv Math，1998，137(1):1－81.

［10］Marsden J E，Shkoller S.Global well－posedness for the agrangian averaged Navier－Stokes(LANS－α)euqations on bounded domains［J］.R Soc Lond Philos Trans Ser A Math Phys Eng Sci，2001，359(1784):1449－1468.