关于分数阶扩散方程的系数反问题
张 维,严春梅,文 进
(成都理工大学 管理科学学院,四川 成都 610059)
0 引 言
Ω 是Rn上的一个有界域,n ≥1,并且具有光滑的边界Ω.考虑如下初边值问题,


其中,Γ 为Gamma 函数,满足,


如果α >0,则满足ℓ-1 <α <ℓ,ℓ ∈N.当α= 1,2 时,此算子相当于抛物线和双曲线方程.
式(1)是非均匀介质中的反常扩散模型,可以由连续时间随机游动得到.有研究认为,分数阶扩散方程是不常用的,它包括了分数阶扩散方程的一个参数阶α.显然,它违反了高斯在实验中的普遍情况,不遵循高斯预测[1].文献[2- 5]对初边值问题(1)~(3)也有所研究,例如,在p ∈C(Ω—)和p ≤0 在Ω 上的条件下,有如下结论:
1)当0 <α <1 时,如果a ∈H2(Ω)∩(Ω),方 程 存 在 唯 一 解,u ∈ C([0,∞);H2(Ω) ∩(Ω)).此外u ∈C([0,∞);L2(Ω)).
2)当1 <α <2 时,如果a ∈H2(Ω)∩(Ω),方程存在唯一解,u ∈C([0,∞);H2(Ω)∩(Ω)∩C1([0,∞);L2(Ω)).此 外,u ∈C([0,∞);L2(Ω)).
固定a ∈H2(Ω)∩(Ω),由u(p,α)= u(p,α)(x,t)表示为式(1)~(3)的解.所给系数p 的初边值问题称为正问题.实践中,系数p 和分数阶导数的阶α 经常是未知的,必须通过解的可用数据来确定.这就是一个系数反问题.
对于当α = 1,2 时的系数反问题,即双曲线和抛物线类型的偏微分方程,可利用由Bukhgeim 和Klibanov 创建的方法[6],其方法是求解偏微分方程反问题的常用方法,其基于Carleman 估计的加权L2-估计.然而,对于分数导数,αN 并不适合分部积分法的一般步骤,所以对于分数阶扩散方程(1),不能直接证明Carleman 估计.当α = 1/2,1/3时,在一维的情况下,可以减少偏微分方程(1)中导数x,t 是自然数的阶数,建立Carleman 估计.Cheng[7]证明了在一般情况下,当α = 1/2 时的Carleman 估计,但是对于一般的α,Carleman 估计的证明仍然是很难的.因此,除α = 1/2 时或其他特殊的α 值以外,即使在一维情况下,系数反问题都没有结果.
本研究的目的是通过数据u |w×(0,T)(T >0,w⊂Ω 是恰当的子域)来证明式(1)中系数反问题,p(x),x ∈Ω 和α ∈(0,1)∪(1,2),的唯一性.所提供的数据,u|w×(0,T)不仅能够确定p(x),还能确定阶数α.
1 符号与引理

对于任意给的常数M >0,光滑函数η,有,

引理1 如果A 随着增长阶,‖Cos(s)‖ℓ(x)≤Meθs,s ≥0,生成一个余弦算子函数Cos,对于分数阶扩散问题,α
t φ(t)= Aφ(t),t >0,φ(0)= a,α∈(0,2),是适定的,其解算子满足增长阶‖Sα(t)‖ℓ(X)≤Mαeθ2/αt,t ≥0,表达式为,
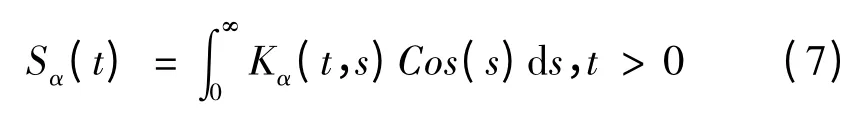
这里的内核Kα定义是依赖以下的Wright 函数Φγ,

引理2 α ∈(0,2),f(t),t ≥0 是在Banach 空间X 中的函数且满足,‖f(t)‖≤Meθt,t ≥0.f 随着式(8)定义的核Kα转换,定义为,

引理3[9]如果0 <α <2,β 是任意的常数,μ是任意的实数,满足则对于任意的p ≥1,有以下展开式,

2 定理与证明
定理1 α,β ∈(0,1)∪(1,2),假定式(5)、(6)成立,且p,q ∈UM.
1)如果在w ×(0,T)中,u(p,α)= u(q,α),则在Ω 中,p = q.
2)假设a ≤0,或者a ≥0,或者a ≠0.如果在w ×(0,T)中,有u(p,α)= u(q,β),则在Ω 中,有α= β 且p = q.
证明 令w = w(p)是以下方程的解:

由式(5)和p ∈W1,∞(Ω),可以得到,

由引理1,当x ∈Ω 且t >0 时得,

和

假设,

由解t 的解析性[10],可得,

因此,

对任意的x ∈w,由引理2 得,

由式(13)和p,q ∈W1,∞(Ω),在Ω 中可以得到p = q.因此定理1 的第一部分得到证明.
假设在w × (0,T)中,u(p,α)= u(q,β).由解t 的解析性可得,

因 为,p ∈ W1,∞(Ω), 通 过(Apu)(x) =-△u(x)- p(x)u(x)和D(Ap)= H2(Ω)∩(Ω),定义一个算子,Ap∈L2(Ω).设{λk}k∈N和{μk}k∈N是算子Ap和Aq所有特征值的集.注意λk,μk>0,且从L2(Ω)到 它 自 身 是 有 界 的.则,{φkj}1≤j≤mk和{Ψkj}1≤j≤nk,k ∈N 是Ker(Ap- λk)和Ker(Aq- μk)的标准正交基,每一个{φkj}k∈N,1≤j≤mk和{Ψkj}1≤j≤nk在L2(Ω)中都是标准正交基.(·,·)是L2(Ω)中的内积.则有,
u(p,α)(x,t)

和,

由式(5)知级数在C([0,∞);H2(Ω)∩(Ω))中是收敛的.
由引理3,当t →∞时可得,

和,

其中,Γ(1-α)≠0,且-1 <1-α <1,1-α ≠0.
此外,在Ω 中易得,

和,

由式(14),当t →∞时有,

| (A-1pa)(x)| =| b(x)| >0,x ∈Ω.
同理,对于x ∈Ω,有| (A-1qa)(x)| >0.固定,和且cp≠0,cq≠0.由式(15),当t →∞时得,

若α ≠β,不失一般性,假设α <β,等式两边同乘以tα得,

当t →∞时,由tα-β,tα-2β→0 可得cp= 0,矛盾.因此,α = β.由此,定理1 第二部分的证明简化为第一部分的证明,即定理得证.
3 结 论
本研究考虑分数阶扩散方程系数反问题,讨论了空间系数p(x),x ∈Ω 的反问题并通过数据u|ω×(0,T)确定分数阶导数的阶数α,并证明了p(x),x∈Ω 和α ∈(0,1)∪(1,2)的唯一性.
[1]Metzler R,Klafter J.The random walk's guide to anomalous diffusion:a fractional dynamics approach[J].Phys Rep,2000,339(1):1-77.
[2]Li Z.Non-symmetric linear diffusion equation with multiple time-fractional derivatives[D].Tokyo:The University of Tokyo,2013.
[3]Luchko Y.Maximum principle for the generalized time-fractional diffusion equation[J].Math Anal Appl,2009,351(1):218-223.
[4]Luchko Y.Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation[J].Comput Math Appl,2010,59(5):1766-1772.
[5]Sakamoto K,Yamamoto M.Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems[J].Math Anal Appl,2011,382(1):426-447.
[6]Bukhgeim A L,Klibanov M V.Global uniqueness of a class of multidimensional inverse problems[J].Sov Math Dokl,1981,24(2):244-247.
[7]Cheng J,Lin C,Nakamura G.Unique continuation property for the anomalous diffusion and itsapplication[J].Differ Eqns,2013,254(9):3715-3728.
[8]Bazhlekova E.Fractional evolution equations in Banach space[D].Enghoven:Technische Universiteit Eindhoven,2001.
[9]Podlubny I.Fractional differential equations[M].San Diego,CA:Academic Press,1999.
[10]Sakamoto K,Yamamoto M.Initial vale/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems[J].Math Anal Appl,2011,382(1):426-447.

