改进生物地理学优化算法的无线传感器节点定位

马世欢，张亚楠

改进生物地理学优化算法的无线传感器节点定位

马世欢，张亚楠

节点定位是无线传感器网络的应用基础，针对DV-Hop算法定位误差的缺陷和提高节点的定位精度，提出一种生物地理学优化算法的无线传感器节点定位方法。首先，对标准生物地理学优化算法进行改进，提高其全局搜索能力，然后，利用改进生物地理学代替DV-Hop算法第三阶段的最小二乘算法，对节点定位结果进行优化，最后，在Matlab 2012平台上对算法的定位性能进行仿真分析。仿真结果表明，相对于DV-Hop算法，其算法提高了节点的定位精度，大幅度降低了节点的定位误差，具有更高的实际应用价值。

无线传感器网络；节点定位；生物地理学优化算法；平均跳距

0 引言

随着无线技术和通信技术的发展，无线传感器网络（wireless sensor network，WSN）应运而生，其广泛应用于国防军事、抢险救灾、环境监测、预防控制、仓库管理、维护秩序等领域[1]。在实际应用中，没有位置消息的数据没有什么任何价值，因此对节点进行高精度的定位已经成为当前无线传感器网络研究中的重点[2]。

针对无线传感器网络节点定位问题，国内外许多研究团队和研究机构进行了广泛、深入研究，提出了许多有效的传感器节点定位算法。现阶段节点定位算法主要分为两类：基于测距（Range-based）[3]和基于非测距（Range-free）[4]。测距算法主要包括：接收信号强度、到达时间和到达角度等[5-7]，它们受环境因素影响较大，定位结果不稳定，而且定位结果与测距设备直接相关，定位成本高，鲁棒性差，定位精度低[8]。非测距算法主要通过少量锚节点对未知节点实现定位，定位成本低，其中DV-Hop算法作为最具代表的非测距算法，在无线传感器定位中得到了广泛应用[9]。但是基本DV-Hop算法存在受网络拓扑结构影响大，定位误差大，精度低等不足，为此，许多学者对DV-Hop算法的工作原理进行了分析，对其不足进行了相应改进，如文献[10]对锚节点每一跳距的计算方式进行了改进，减小了平均跳距的计算误差，提高了节点的定位精度；文献[11]将未知节点看作虚拟锚节点，提高了锚节点的密度，但其存在累计误差比较大的缺陷；文献[12]在计算平均每跳距的基础上，采用如粒子群、遗传算法等对未知节点的定位结果进行了优化，定位结果得到了改善。生物地理学优化（biogeography-based optimization，BBO）算法是一种新的群智能算法，相对于其它群智能算法，BBO算法具有简单、调节参数少等优点，成功应用于优化问题求解中[13]。

为了改善无线传感器节点的定位效果，针对DV-Hop算法的不足，提出一种BBO算法优化DV-Hop的无线传感器网络节点定位算法（BBO-DVHop），并通过仿真实验对算法的性能进行测试和分析。

1 生物地理学优化算法

1.1 标准BBO算法

2008年，Simon等提出了生物地理学（BBO）算法，其模拟自然界的种群相邻个体迁移和特别个体的突变过程对信息进行更新，从而找到问题的全局最优解[14]。

1.1.1 迁移率

设第s个栖息地物种数量为s，那么物种迁入和迁出率计算公式（1）：

式中，λ和μ分别为迁入率和迁出率；I和E分别表示最大迁入率和迁出率。

1.1.2 突变率

根据物种数量s、概率Ps对特征变量进行突变，突变概率函数的计算公式（2）：

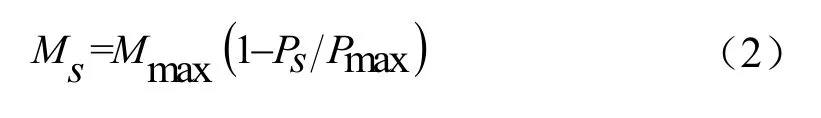
式中，Mmax为最大突变率；Pmax=arg(max(Ps))，s=1,2,…,n，Ps计算化式为公式（3）：

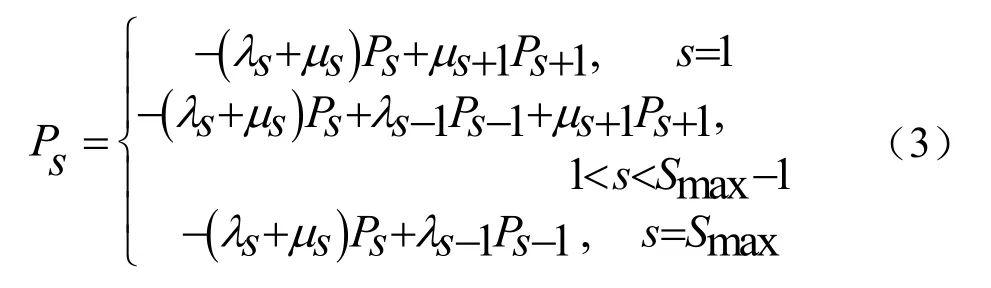
1.2 生物地理学优化算法的改进

BBO算法存后期收敛速度慢、易陷入局部最优等不足，为此，本文对BBO算法进行相应的改进，以提高其全局搜索能力。

（1） BBO算法采用线性迁移模型计算迁入率λ和迁出率 μ，导致算法的收敛速度比较慢，为此，采用余弦迁移模型替代线性迁移模型，具体如公式（4）：

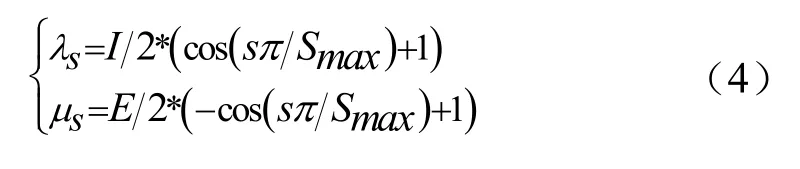
（2）首先根据λi选择需要迁入的栖息地Xi，确定Xi后，根据μj选择需要迁出的栖息地Xj；然后从Xj中随机地选择SIV替代Xi中相应的SIV，最后对迁移算子进行加权，那么迁移算子变为公式（5）：

式中，α是随机数。

2 BBO-DVHop算法

2.1 DV-Hop算法

（1）计算未知节点与锚节点的最小跳数。在无线传感器网络，每个锚节点广播自身分组信息：{(ID,(x,y),hop)给邻居节点，且hop=0；当未知节点接收到一个锚节点的分组信息后就保存该锚节点的最小跳数，并将 hop=hop+1转发给邻居节点，若该分组信息来自同一锚节点，则忽略，这样全部节点可以保存任一锚节点间的最小跳数。

（2）估算未知节点的平均每跳距离。设锚节点i,j的坐标分别为(xi,yi)，(xj,yj)，i与j之间的最小跳段数为hopj，任一锚节点的平均跳距计算公式为公式（6）：

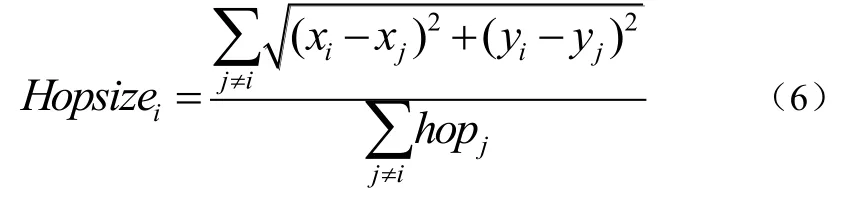
未知节点接收、保存锚节点在网络中广播的自身平均每跳距离，且仅保存其接收到的第1个数值，继续转发该跳距，以保证尽可能多的未知节点保存平均跳距是从离其最近的锚节点处获得[15]。

（3）计算未知节点位置。设与未知节点 D(x,y)可以直接通信的锚节点为：并假设步骤（2）中计算未知节点 D(x,y)与相应锚节点距离分别为d1,d2,···dn，那么如公式（7）：

可表示为线性方程组AL+ε=b，ε为机误差向量，

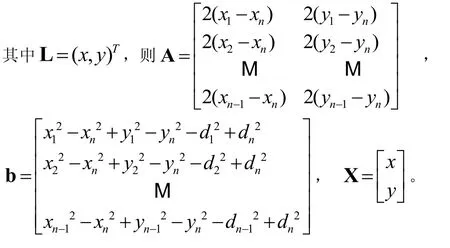
采用最小二乘算法求得方程的解为公式（8）：

2.2 DV-Hop算法存在的不足

在DV-Hop定位算法中，选择具有最小折点的几个跳段为未知节点与锚节点之间的直线段，那么该折线段中各点越接近共线，误差越小。由于网络中节点随机分布，共线概率较低，误差必然存在。dn是由未知节点到锚节点的估算平均跳距与最小跳数乘积等效替代，包含很大的误差，向量b的每个元素均包含测量距离dn，而dn却包含很大的误差，因此根据式(8)求得的未知节点坐标精度相对较低，为提高定位精度，将问题转化为优化估算距离dn的问题。

设未知节点 D(x,y)到锚节点 A1,A2,L ,An的实际距离为 r1,r2,L,rn，相应的测距误差为 ε1,ε2,L ,εn，应满足式(7)可转换为公式（9）：

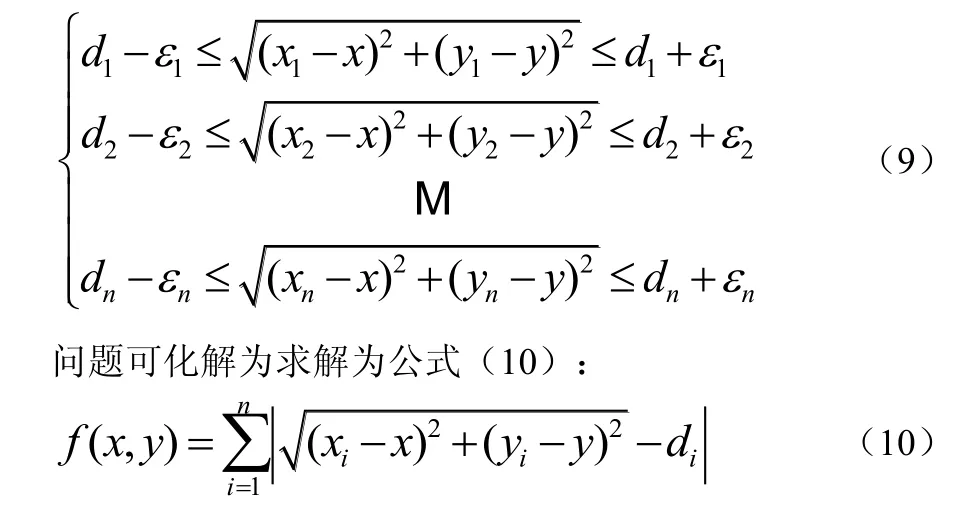
当式（10）取得最小值时，未知节点的估计坐标最接近真实坐标，定位误差最小，本文采用生物地理学优化算法对式（10）进行求解，以提高节点定位精度。

2.3 BBO对定位结果的优化步骤

为了进一步提高无线传感器节点定位精度，利用 BBO算法的全局搜索能力，对DV-Hop算法定位结果进行优化，具体步骤如下：

（1）设未知节点D(x,y)与其相邻的锚节点数为num。

（2）根据式（7）计算 num个相邻锚节点的坐标值以及与未知节点D(x,y)的距离，建立式（9）的约束条件。

（3）初始化BBO算法的相关参数，并随机初始化适宜度向量xi，i=1,2,…,NP，每个向量对应未知节点D(x,y)位置的可行解。

（4）根据适应度函数计算栖息地i的适应度值，并计算栖息地i对应的物种数量si、迁入率λ和迁出率μi，i=1,2,…,NP，适应度函数定义如公式（11）：

（5）对栖息地的SIV进行调整，并重新计算栖息地的适应度值。

（6）更新概率 Ps和突变率，并重新计算栖息地的适应度值。

（7）如果满足终止束条件，保存最优的适宜度向量，反之，则返回步骤(4)继续优化。

（8）根据最优适宜度向量得到未知节点D(x,y)的位置。

3 仿真实验

3.1 仿真参数

为了验证BBO-DVHop算法的有效性，在Matlab 2012平台选择DV-Hop算法进行对比仿真实验。采用平均定位误差(error)作为定位结果评价标准，error计算公式为公式（12）：

表1 仿真实验参数

3.2 结果与分析

3.2.1 测距误差对定位结果影响

当在节点的测距误差发生变化的情况下，DV-Hop、BBO-DVHop算法的平均定位误差变化曲线如图1所示：

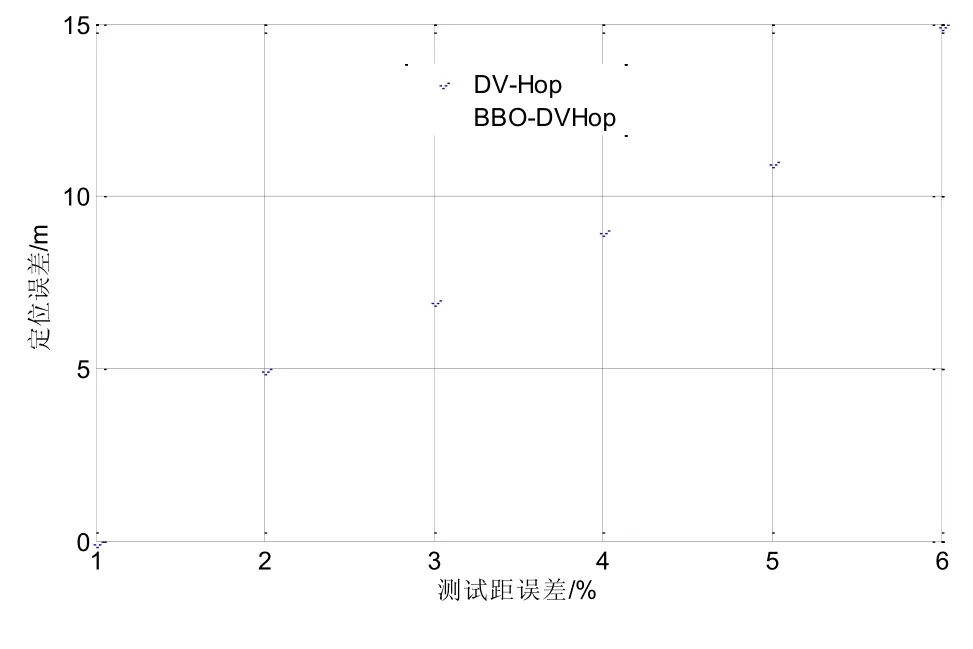
图1 测距误差对定位结果的影响

从图 1可以看出，随着测距误差的增加，DV-Hop、BBO-DVHop的平均定位误差随之增加，这主要由于定位误差不断的累计影响了未知节点的定位精度。BBO-DVHop算法由于采用BBO算法对DVHop算法的定位结果进行优化，可以较好地抑制节点测距误差累计的干扰，因此，在相同测距误差条件下，BBO-DVHop算法的定位精度要高于PSO-DVHop算法，从而对测距误差具有更好的鲁棒性。

3.2.2 锚节点数对定位结果影响

锚节点数量为5～40的情况下，DV-Hop、BBO-DVHop的平均定位误差仿真结果如图2所示：

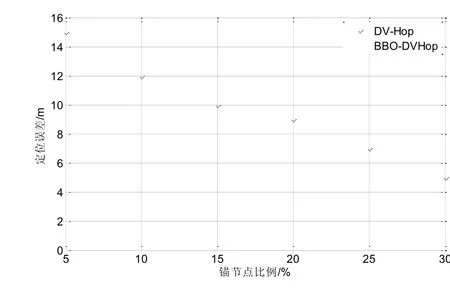
图2 不同数量锚节点的平均定位误差比较

从图2可知，随着锚节点的增加，DV-Hop、BBO-DVHop的平均定位误差下降，这主要是由于锚节点数的增加，节点的平均定位精度相应提高。当锚节点数量相同时，BBO-DVHop算法的平均定位误差小于DV-Hop算法，当锚节点数量大于20后，BBO-DVHop算法的优势更加明显，对比结果表明，BBO-DVHop提高了节点的定位精度，在相同定位精度要求，可以大幅度减少锚节点的数量，有效降低了节点的定位成本。

3.2.3 通信半径对定位结果影响

不同通信半径条件，可以选择邻居节点数是不相同的，当节点的通信半径发生变化时，DV-Hop、BBO-DVHop的平均定位误差仿真结果如图3：

图3 不同通信半径的平均定位误差对比

从图3可以明显看出，随着通信半径的增大，DV-Hop，BBO-DVHop算法的定位误差不断减小，这主要是由于随着通信半径的增加，节点获得邻居锚节点的概率增加，定位的精度得以提高，同时，在相同通信半径条件下，BBO-DVHop的定位误差小于DV-Hop算法，具有一定的优势。

4 总结

针对传感器节点定位问题，在分析DV-Hop算法存在的不足基础上，提出一种BBO算法优化DV-Hop定位结果的感器节点定位算法，并针对标准BBO算法存在的不足进行了改进，最后采用仿真对比实验对算法的定位精度、平均定位速度进行了分析，仿真实验结果表明，相比于DV-Hop算法以及其它改进DV-Hop算法，BBO-DVHop提高了传感器节点的定位精度，降低了定位计算过程中的复杂度，是一种简单、实用的无线传感器节点定位方法。

[1]王汝传,孙丽娟.无线传感器网络技术及其应用[M]. 北京:人民邮电出版社,2011.

[2]孙利民,李建中,陈瑜,等.无线传感器网络[M].北京:清华大学出版社,2005: 135-155.

[3]Garg V, Jhamb M. A Review of wireless sensor network on localization techniques [J]. International Journal of Engineering Trends and Technology,2013, 4(4): 1049-1053.

[4]王福豹,史龙,任丰原.无线传感器网络中的自身定位系统和算法[J]. 软件学报, 2005,16(5):857-858.

[5]Bulusu N, Heidemann J, Estrin D. GPS-less low cost out door localization for very small devices [J]. IEEE Personal Communication, 2000, 7(5):28-34.

[6]安文秀, 赵菊敏, 李灯熬. 基于Amorphous的无线传感器网络定位算法研究[J].传感器与微系统 2013, 32(2): 33-35.

[7]王珊珊,殷建平.求解无线传感器网络定位问题的线性规划算法[J].计算机研究与发展2009,46(5): 705-712.

[8]毛科技,赵小敏,何文秀等.WSN中基于区域划分的半自动DV-Hop定位算法[J].计算机科学,2012,39(3): 39-42.

[9]衣晓,王梓有,薛兴亮.一种基于次锚节点的无线传感器网络质心定位算法[J].计算机应用与软件,2013, 30(6):116–120.

[10]陈星舟,廖明宏,林建华.基于粒子群优化的无线传感器网络节点定位改进[J].计算机应用,2010, 30(7): 1736-1739.

[11]赵仕俊,孙美玲,唐懿芳.基于遗传模拟退火算法的无线传感器网络定位算法[J].计算机应用与软件,2009, 26(10):189-192.

[12]Zhao Yan Huang, Qian Zhi Hong, Shang Xiao Hang. PSO localization algorithm for WSN nodes based on modifying average hop distances [J].Journal on Communications, 2013, 34(9):105-114.

[13]赵吉,付毅,梅娟.基于粒子群算法的改进 DV-Hop定位算法[J].计算应用与软件, 2012,29(12):69-72.

[14]高凯歌, 郑向伟. 基于中值迁移和柯西变异的生物地理学优化算法[J].计算机工程与设计,2013,34(4): 1292-1295.

[15]李辉,熊盛武,刘毅,等.无线传感器网络 DV-Hop定位算法的改进[J].传感技术学报,2011,24(12): 1782-1786.

Node Localization Based on DV-Hop Optimizing by Improved Biogeography-based Optimization Algorithm

Ma Shihuan, Zhang Yanan
(Department of Computer Engineering, Henan Polytechnic Institute, NanYang 473000, China)

Node localization is a basic application of wireless sensor network. Aiming at the defects of DV-Hop algorithm of positioning error and the improvements of node positioning accuracy, this paper proposes a node localization algorithm of wireless sensor with biogeography-based optimization. Firstly, the standard biogeography-based optimization algorithm is improved to obtain a better ability to do global search, and then replace the less squares algorithm in the third step of DV-Hop with the improved biogeography-based optimization to improve the results of node localization. Finally, simulate and analyze the localization performance of this algorithm on the Matlab 2012 platform. The simulation results show that, compared with DV-Hop algorithm, the proposed algorithm improves the localization accuracy of nodes and reduces the positioning error greatly. It has higher value for practical application.

Wireless Sensor Networks; Node Localization; Biogeography-based Optimization Algorithm; Average Hop Distance

TP311

A

2014.04.23）

1007-757X(2015)05-0050-04

马世欢（1976-），男，河南南阳人，河南工业职业技术学院，计算机工程系，讲师，硕士，研究方向：软件技术，南阳，473000张亚楠（1985-），女，河南南阳人，河南工业职业技术学院，计算机工程系，讲师，硕士，研究方向：计算机应用，南阳，473000