基于平衡理论的P2P信任模型的设计

周晓燕

基于平衡理论的P2P信任模型的设计

周晓燕

当前P2P网络中存在着大量的恶意节点攻击和共谋团体欺骗等问题，已存在的信任模型一定程度上完善了P2P网络环境，但模型的侧重点不同，无法全面解决大规模的恶意攻击和欺骗。为此，提出了基于平衡理论的 P2P信任模型。该模型由信任结构的构建、恶意节点检测和信任推测等3部分完成。首先，根据平衡理论构建信任网络；针对恶意节点的攻击，利用平衡理论定义节点的平衡因子，通过计算恶意行为对网络平衡性的影响来检测恶意节点；最后，利用信任推测算法来推测信任节点，防止网络加入不信任的节点，降低网络的安全性。实验结果表明，该模型可靠完善，算法有效和健壮。

P2P；信任模型；平衡理论；恶意攻击

0 引言

随着互联网技术的不断发展，P2P技术在日常网络应用中起着不可或缺的作用。P2P网络与传统C/S模式网络相比具有对等性、开放性等特点。为各个领域的应用发展带来了极大的便利，但相对的开放和对等使得 P2P网络面临着一些前所未有的安全问题，例如节点恶意攻击、共谋团体欺骗、恶意病毒的传播以及知识产权保护等问题[1]。

近几年来，国内外许多学者对建模 P2P网络环境中的信任模型展开了广泛的研究，并在一定程度上取得了显著的成果。目前，用于构建P2P网络的信任模型主要分为4类，分别是：基于局部历史信息的信任模型、基于全局历史信息的信任模型、基于信任证据链传递的信任模和基于历史信息相关性的信任模型。

基于局部历史信息的信任模型是通过网络中一个节点与另一个节点的历史通讯信息计算该节点对其他节点的信任。该模型依赖于其他节点的一些历史数据信息，无法避免恶意节点或恶意团体对信任值计算的影响，虽然模型中存在检测恶意团体的方法，但从整体看，这种方法存在着较大的局限性，很难避免一些恶意行为[2-3]。

基于全局历史信息的信任模型使用全网络的通讯历史信息来计算节点的信任值。虽然信任值计算可靠但对全网的通信带宽有较高要求且算法的效率也较低[4]。

在基于信任证据链传递的信任模型中，每个节点都维护着一个与自身有交互的其他节点的评价信息，算法在节点之间找到所有的路径，并添加权重来进行信任值计算。这种方法在直接信任和间接信任不明确时无法满足建模要求，并且方法在计算权重时通信开销和查询效率也存在一定的不足[5]。

基于历史信息相关性的信任模型是利用节点之间的相关程度与全局模型进行结合，对节点团队恶意行为有一定的抵制能力，其相关性因子只考虑了通讯成功、失败参数，并没有其他优先级别、延时级别、可靠性级别、峰值吞吐量级别、平均吞吐量级别等参数[6]。

针对上述模型中的不足，本文提出了基于平衡理论的P2P信任模型。模型由3部分构成：信任结构的构建、恶意节点检测和信任推测。此信任模型一方面，使 P2P网络抵御恶意节点和恶意团体的共谋等行为的攻击；另一方面，可以在新节点加入网络时进行信任推测，已禁止不信任节点的加入，提高了信任网络的准确性、健壮性。

1 基于信任结构的P2P网络建模

1.1 信任结构的构建过程

在信任结构的构建过程中，需要根据平衡理论提取出网络中的节点，并根据节点之间原有的关系对它们进行组合，最终形成一个信任网络。根据海德平衡理论，将 P2P网络中的节点作为构造三角形的顶点，每个节点与其他两个相邻节点之间有“信任”或“不信任”的关系，节点之间的“信任”关系用“+1”表示，而“不信任”关系使用“-1”表示，这样可以构成3个节点的三角形结构。

根据所构造的三角形是否处于平衡状态，来判断三个节点之间是否可信。由平衡关系的判断方法，我们可以得出T1和T3两种类型的平衡状态，如图1所示：

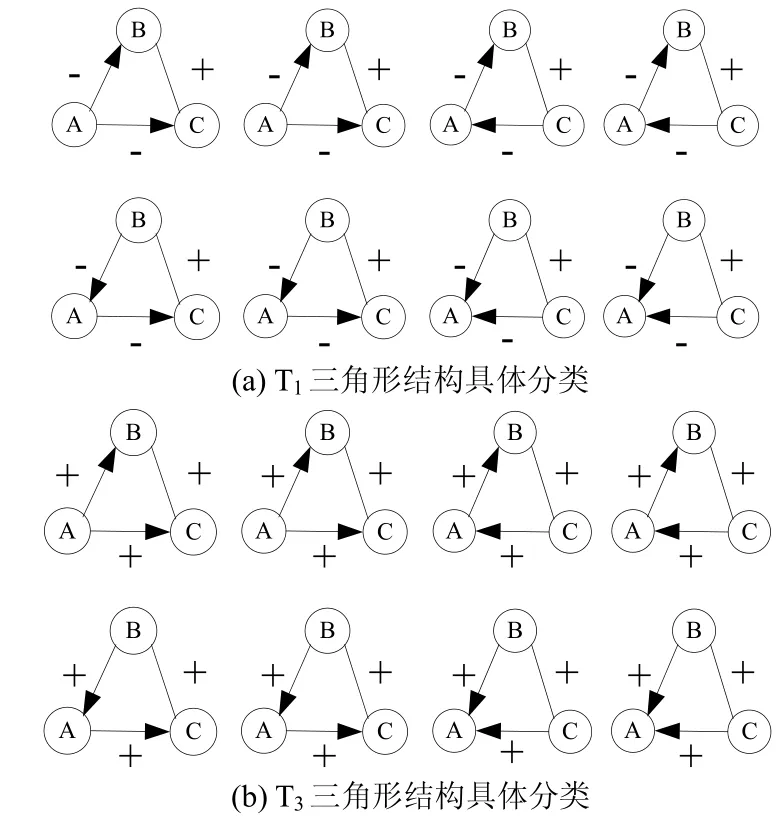
图1 处于平衡状态的三角形结构

然后，提取图1中16种情况的三角结构节点，再将其组合进而形成信任网络。下面对基于 T3平衡状态构建信任结构的过程进行说明，基于 T1平衡状态构建信任结构的方法以此类推。

将图1(b)中的三角形结构进行进一步地整合，可以得到的分类结果如图2所示：

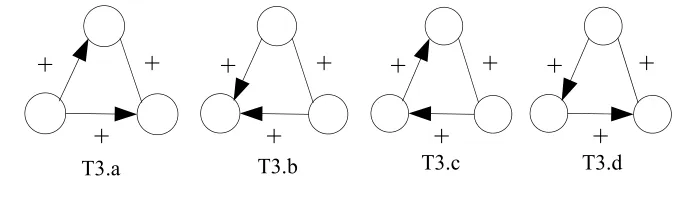
图2 T3三角形结构整合结果

网络中节点与节点之间的关系利用邻接矩阵 E进行表示，E中记录了数据集中符号为“+”的链接集合。矩阵E中的元素用ex,y表示，其中x和y表示元素所在的行和列。若两个节点x、y之间存在符号为“+”的链接，则该ex,y的值为1，否则值为0。

为了在P2P网络中找到满足T3a或T3b结构的节点，定义满足T3结构的三角形集合S3。首先在邻接矩阵E中挑选两个位于同一行或列，且ex,y值为1的元素，进而得到两个节点分别记为（x，y1）、（x，y2）或（x1，y）（x2，y）。然后，在矩阵E中确认的值是否为1，若为1则将节点x1,y1,y2或y2,x1,x2之间的链接信息加入到S3中，S3的集合表示如公式（1）：

重复上述两个步骤，使每一行或列中所有可能的取值一一验证，最终得到满足T3a或T3b平衡结构的节点集合S3。

而对于T3.c和T3.d两种结构，从矩阵的第x行选取值为1的一个元素 ex,y1，第x列选取值为1的一个元素ex1,x，其下标记为(x,y1)和(x1,x)。然后，根据E中的数据检验元素 ex1,y1或 ey1,x1的值是否为 1，若为 1则将节点x,x1,y1之间的链接信息加入到集合S3中。

重复上述步骤，直到每一行及每一列所对应的可取元素全被检验后，就得到了包含完整节点链接信息的集合S3。

以此类推得到集合S1。最后将集合S1和S3进行合并。将数据信息以网络的形式展现出来，即得到了一张信任网络。

1.2 基于信任结构的恶意节点检测

1.2.1 单个恶意节点检测

在 P2P网络中，恶意节点最常见的攻击是针对目标节点发布伪造的评价信息，进而提高或降低目标节点的信任值。因此，如果仅使用节点的局部信任值来计算目标节点的信任值，就会使目标节点的信任值受到较大的影响[7]。

针对恶意节点攻击的特点，文中提出了一种基于平衡理论的恶意节点检测方法，首先，利用平衡理论定义节点的平衡因子，进而通过恶意行为对网络平衡性的影响来检测节点，具体的检测方法如下所述：

（1）获得待检测的目标网络 T，针对网络中有直接链接的两节点i和j，检测节点j对节点i的评价行为的异常情况。

（2）对于网络中的节点i，收集信任网络T中节点i所处的三角形结构的信息，根据式（2）计算节点i的平衡因子 βi，该平衡因子反映了该节点i在网络T中的全局性的平衡情况如公式（2）：

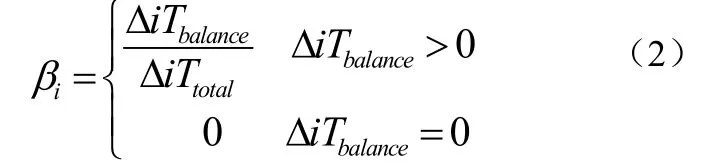
其中， Δi Ttotal为包含节点i的三角形结构的总个数, Δi Tbalance为三角形结构中处于平衡状态的三角形的个数。

（3）针对节点 j到节点i的链接，收集该链接Eji所处的三角形结构，并利用式（3）计算该链接Eji的平衡因子 βji，βji反映了链接 βji在整个信任网络T中的全局性平衡度如公式（3）：

其中，ΔjiTbalance表示三角形结构中处于平衡状态的三角形的个数，ΔjiTtotal节点 j到节点i的链接所处的三角形结构的总个数。

（4）最后利用节点i的平衡因子iβ与链接Eji的平衡因子jiβ，根据式（4）计算节点 j的评价行为如公式（4）：

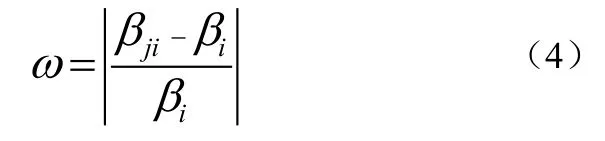
如果ω的值大于或等于选定的阈值，则认为节点 j对节点i的评价属于恶意评价。因此，认为节点 j属于恶意节点；否则属于正常的评价行为。

1.2.2 共谋团体检测

共谋团体被认为是一些具有相似恶意行为的恶意节点的组合，团体的恶意行为会对整个网络造成极大的危害，这不仅降低了网络的可信性，还对 P2P网络的发展造成极大的阻碍[8]。共谋团体的恶意行为的示意图如图3所示：

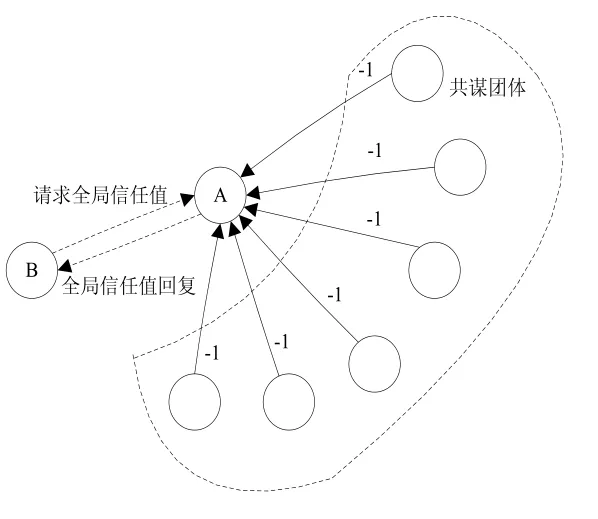
图3 共谋团体的恶意行为

当网络中存在恶意共谋团体时，单个恶意节点的检测方法不在实用。所以本文在单个恶意节点检测的基础上，进一步提出了检测恶意共谋团体的方法。

要检测与节点i相关的恶意团体，首先，在网络中找到与节点i存在历史评价信息的节点集合iL，并定义集合Si为对节点i有恶意行为的节点集合。

（1）检测集合Li中与节点i有恶意行为的信息，若有这样的节点，将其加入到Si中。重复上面的过程，直到集合iL中的所有节点均检测完毕后，即可得到对节点i有恶意行为的节点集合Si。

（2）在集合Si中任取两个节点x,y，得到其共同历史通信节点集合Nxy，然后计算这两个节点间的相关性sim(x,y)如公式（5）：

（3） 若sim(x,y)大于0.8，则将两节点加入共谋团体集合 iC中。待集合Si中所有两两节点组合的相关性值经过计算后，得到了针对节点i的恶意共谋团体iC。

1.3 基于信任结构的信任推测算法

在一般情况下，一个节点认为有价值的评论对另一个节点有一定有参考。例如所有与该节点有直接关系的节点都认为此节点信任可靠，那么此前与此节点毫无关系的新节点也有理由相信此节点信任可靠，如图4所示：

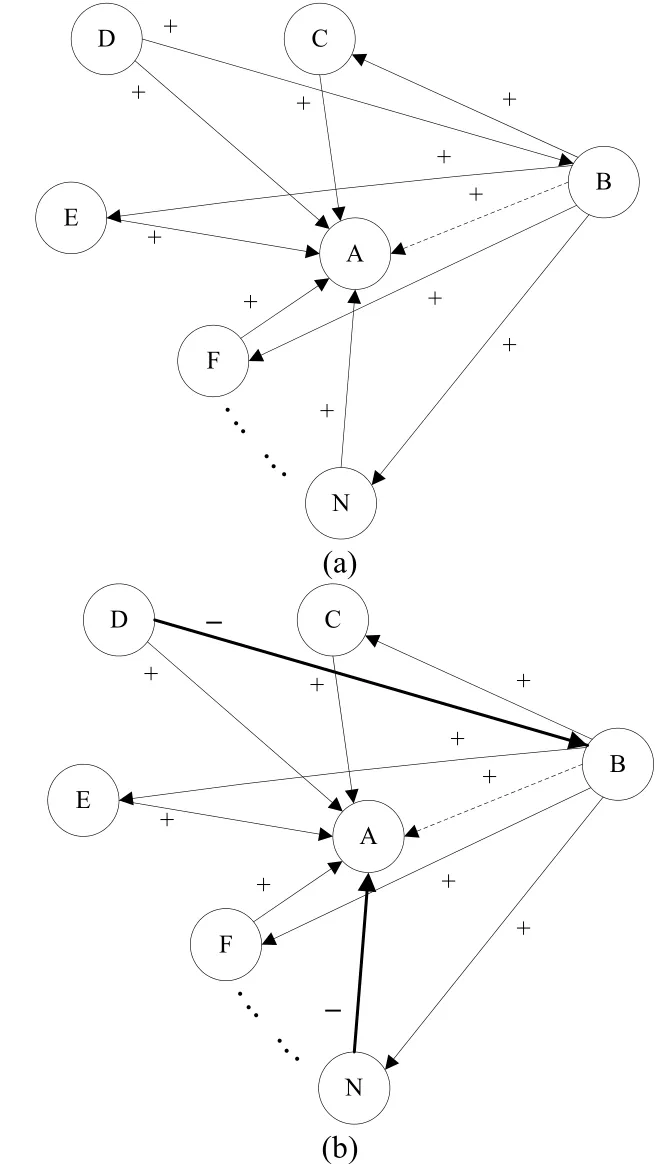
图4 基于全局信息的信任推测

由图4(a)所示可知：与节点B有直接信任关系的节点均与节点A有信任关系，可以推测出节点B对节点A也具有信任关系。在这种情况下，通过一个全局的评价得出了信任推测的结果，从而一个新的节点就可以通过这种信任推测方式来。

在实际的网络环境下，一个目标节点收到的评价既有“信任”也有“不信任”。由图4(b)可知，与节点B具有直接信任关系的节点，对节点 A既有信任关系也有不信任关系，那么在情况下，一个新的节点继续已经不能通过传统的推测方式推测目标节点的可信性。

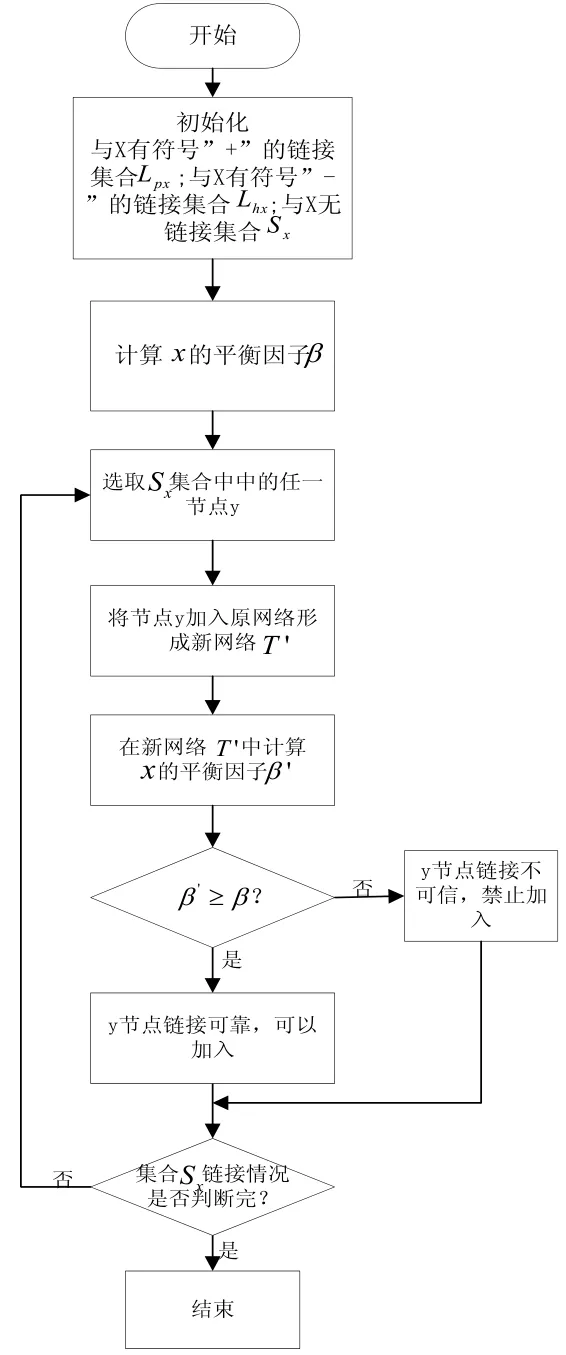
图5 信任推测算法流程图

为了解决上述问题，文中在 P2P信任网络的架构中利用一种基于平衡理论的信任推测算法来推测信任节点。该算法不再依赖用户的全局历史评价、同时对用户的历史通讯也没有了较多限制。算法的核心思想是对原有信任网络的平衡因子β值与加入新节点后所得到的新网络的β值进行比较，得出该新节点是否为可加入信任网络以及与其他节点之间关系。将原始信任网络中源节点的平衡因子记为β，加入新链接后的网络针对源节点的平衡因子记为 'β。根据式（2）计算β与 'β的值，根据比较结果判断新节点是否满足信任推测条件。信任推测算法的流程图如图5所示：由图x5可知：使用基于平衡理论的信任推测算法对网络中节点 进行信任预测，首先，需要进行一系列的初始化操作：初始化与源节点x有符号为“+”的链接集合Lpx，符号为“-”的链接的集合Lhx，以及与节点x没有直接链接的节点集合Sx，根据现有原始网络T的信息，按照公式（2）计算出初始网络中源节点x的平衡因子，进而初始化β。选取集合Sx中选取节点y，将其加入到信任网络T中，得到新的信任网络T'，根据T'的信息通过公式（2）计算出更新后的网络中源节点的平衡因子 β'。若 β'≥β，说明加入节点y的链接后，网络T'的平衡情况较原始网络好，因此，认为y较原始信任网络T相比，新的网络T'也是可信的，节点 的链接满足平衡条件，可以加入；否则若 β'＜β，则说明加入节点y的链接后，网络的平衡情况受到了影响，因此y节点的链接不可信不可加入。重复该过程，直到集合Sx中的所有节点的每种链接情况全部判断完毕。

2 实验结果与分析

2.1 信任网络的建构

本文采用 Epinions数据集对算法的可靠性和健壮性进行验证。在数据集中含有 130,000个节点，节点之间有840,000条链接，其中，链接符号为“+”的数量为710,000，而符号为“-”的链接的数量为130,000。针对Epinions数据集，根据算法的步骤首先建立了存储“+”、“-”链接信息的邻接矩阵E和E'，分别找到原始网络中T3与T1类型的三角形结构。在实验所获得的71,766个节点中，其中包含T3与T1两种平衡三角形结构的具体数量统计信息如表1所示：

表1 T3与T1三角形结构数量统计表

如表1所示，T3结构的三角形数量中第一种链接方向的数量较多，为9,634,044，占实验所得信任网络结果数据中三角形结构总数的比例高达81.28%。而T1三角形结构大部分为第一种链接方向，后两种链接方向形式的三角形总和只占T1类三角形结构总数的28.2%。

为了直观的展示信任建模后信任网络的状况，实验随机抽取 5,000多个节点组成信任网络，符号为“+”的链接用蓝色线条表示，符号为“-”的链接用红色线条表示，而绿色线条表示两节点间符号相反的双向链接。5000节点的信任网络图如图6所示：

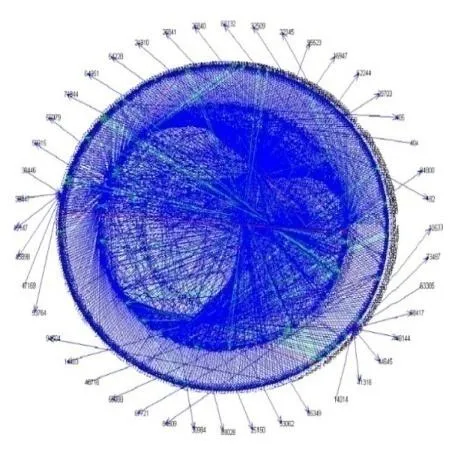
图65000节点的信任网络图

2.2 恶意节点检测结果分析

实验从基于平衡理论建模算法所得到的信任网络中提取出链接数量最多的100个节点，并从该100个节点中随机取出一部分节点，将该部分节点作为目标节点，针对其他节点对这些目标节点的评价进行检测[9]。

实验抽取不同的节点对目标节点行为的恶意性进行检测，从而获得了去除恶意节点前后，目标节点在信任网络中平衡情况的均值。实验统计了22个节点在去除恶意节点前后所在网络平衡性的变化，网络中平衡因子的变化情况如图7所示：

图7 删除恶意节点前、后节点的平衡性对比

图7中下方（曲线2）曲线代表1～22个节点在原始网络中平衡因子值的变化，上方（曲线1）曲线为统计去除恶意节点后节点平衡因子值的均值。从图中可以看到，目标节点的原始平衡因子在0.49～0.96之间，删除恶意链接后对网络的平衡性有一定的影响，但删除恶意节点后节点平衡因子曲线与原始曲线相比有所提高[10]。这说明恶意节点的检测并删除一定程度上增加了网络的可信任性。

2.3 信任推测算法验证

为了验证信任模型中信任推测算法的有效性，在上述实验的基础上，从结果中取出与其他节点链接数最多的 100个节点，并在该100个节点中选取23个节点，每一个节点要求与其余22个节点之间的链接数要大于5。在23个节点所组成的信任网络上进行信任推测实验。所选节点组成的信任网络如图8所示：

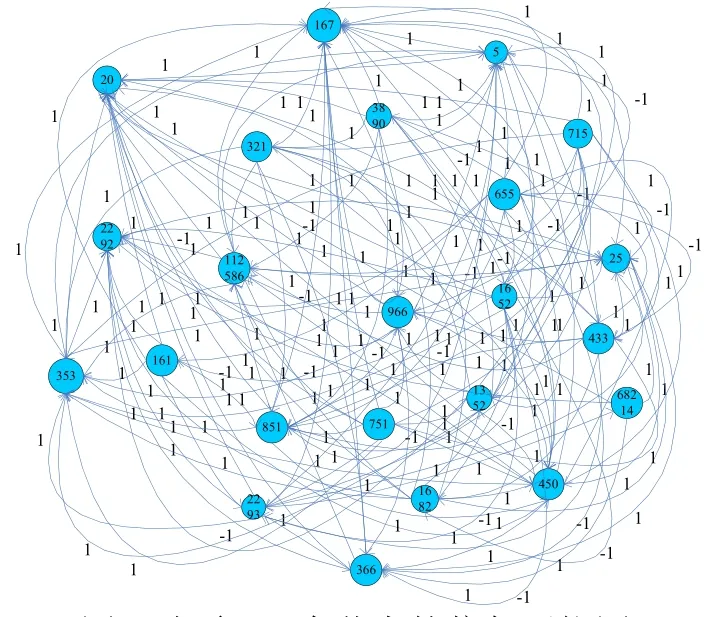
图8 包含23个节点的信任网络图

以图中节点20为例进行信任推测算法验证，首先初始化节点20的初始平衡因子值β20，经过计算得到节点20的初始平衡因子 β20= 0.8768。

从图8中可以看出与节点20没有直接链接的节点集合NS20= {167,321,655,2292}。然后向信任网络中分别添加链接 L20,167= {20,167,1/- 1}、 L20,321= {20,321,1/-1}、 L20,655= {20,655,1/-1 }和L20,2292= {20,2292,1/-1}，进而计算添加链接后新网络中节点20的平衡因子。与的对比信息如表2所示：

表2 节点20的信任推测结果

从表2数据比较可以看出：只有添加链接E20,167和E20,321时，所得的节点20的新平衡因子值＞β20，说明在添加新的符号为“+”的链接后，节点20在网络中的平衡性有所提高，从而推出该链接满足信任推测条件。实验结果表明信任模型中信任推测算法有效可行。

3 总结

本文提出了一种基于平衡理论的 P2P信任模型。模型首先根据平衡理论构建信任网络；然后根据所构建的信任网络进行恶意节点和共谋团体的检测，从而使信任模型能够抵御恶意节点与恶意团体的攻击；最后利用信任推测算法来推测信任节点，以防止网络加入不信任的节点，进一步增强信任网络的安全性。本文创新性地将平衡理论应用到 P2P信任网络的建模中，并利用Epinions数据集对模型的3部分进行数据测试。实验结果表明本文所提出的信任模型安全可靠。

[1]陈姝,方滨兴,周勇林. P2P技术的研究与应用[J].计算机工程与应用. 2002,38(12):20-23.

[2]Audun Jøsang, Touhid Bhuiyan. Optimal Trust Network Analysis with Subjective Logic[J]. Proc of the 2nd International Conference on Emerging SecurityInformation SECURWARE '08. 2008, 179-184.

[3]陈爱国, 徐国爱,杨义先. 评价离散度敏感的 P2P交易系统信任模型[J].电子科技大学学2010,39(3):425-426.

[4]孙知信, 唐益慰. 基于全局信任度的多层分组 P2P 信任模型[J]. 通信学报. 2007,28(9):134-140.

[5]秦志光,杨毅,杨磊. P2P 网络中利用推拉模式实现的信誉系统[J].计算机工程与应用.2013,49(5):88-90.

[6]谭振华,王兴伟,程维等.基于多维历史向量的P2P分布式信任评价模型[J].计算机学报.2010,33(9):1726-1727.

[7]汪胡青, 孙知信. P2P 网络中恶意节点控制算法的研究[J].计算机工程.2012,38(17):142-143.

[8]苗光胜,冯登国. P2P信任模型中基于行为相似度的共谋团体识别模型[J].通信学报.2009,30(8):9-11.

[9]谭振华,王贺等. 基于通信历史相关性的P2P网络分布式信任模型[J].东北大学学报(自然科版).2009,30(9): 1243-1248.

[10]姜守旭,李建中.一种 P2P电子商务系统中基于声誉的信任机制[J].软件学报.2007,34(10):56-57

Design of P2P Trust Model Based on Equilibrium Theory

Zhou Xiaoyan
(Information Engineering Department of Karamay Vocational and Technical College, Karamay833600, China)

There are a large number of malicious attack nodes and collusion groups in P2P network. The existing trust models have perfected the P2P network environment to some extent. But the emphases of the models are different, so they are unable to fully solve large-scale malicious attacks and deception. Therefore, this paper presents a P2P trust model based on equilibrium theory. The model is composedof construction of the trust structure, the malicious node detection and trust speculation. The model constructs trust network according to the equilibrium theory firstly. For malicious nodes attack, it uses the equilibrium theory to define the balance factor of nodes and detects malicious nodes by calculating the impact of malicious behavior on the network. Finally use trust inference algorithm to estimate trust nodes, and prevent network nodes form the involvement of distrust nodes which reduces network security. Experimental results show that the model is perfect and reliable and the algorithm is efficient and robust.

P2P ; Trust Model; Equilibrium Theory; Malicious Attacks

TP393

A

2015.02.02）

1007-757X(2015)05-0021-05

周晓燕（1979-），女，河北冀州，克拉玛依职业技术学院，信息工程系，讲师，硕士，研究方向：计算机网络安全，克拉玛依，833600