基于多维尺度向量的用户兴趣模型构建研究

王庆福

基于多维尺度向量的用户兴趣模型构建研究

王庆福

用户的兴趣模型构建在个性化平台上有着广泛的应用，针对用户的兴趣进行服务定制具有非常重要的意义。提出以多维尺度向量的方式来表征用户的兴趣，多维尺度向量可以较好的反映用户兴趣特征。同时，用户的兴趣随着时间的变化呈现非规则性变化，多维尺度向量可以通过各维度上坐标反映这种非规则变化。实验选取10名志愿者，以新浪网作为兴趣采集资源，实验结果表明，新的算法能够较为准确地反映用户的兴趣变化。

多维尺度向量；用户兴趣；动态非规则；兴趣模型

0 引言

用户兴趣的采集一直是诸多电商平台和社交平台研究热点，针对用户的兴趣进行定向资源推荐，提高用户体验具有非常重要的意义和价值[1]。

用户兴趣的表示一直是用户兴趣采集中的核心问题，如何对用户的兴趣进行定量表示从而根据兴趣特征进行资源定向推荐。传统的兴趣表示方式将用户的兴趣归为一主要兴趣，以此兴趣点来对用户进行定向推荐，显然这种方式不能很好的反映的兴趣特征和兴趣变化[2]；此后，尝试将用户的兴趣按照向量进行表示并定期更新，然而却忽略了用户的动态非规则变化特性[3]，因此，此种方式的兴趣表示方法无法适时的调整用户的兴趣特征。

本文通过分析用户兴趣的动态变化特性，提出采用多维尺度向量来表示用户的兴趣，多维尺度向量中每个维度对应用户的一个兴趣维度，定义兴趣衰减函数来对用户兴趣的动态非规则变化进行量化表示，当用户的某个兴趣维度衰减到临界阈值时，可对用户的多维尺度兴趣向量进行全局调整去掉该兴趣维度。实验以新浪网作为用户兴趣的资源采集，挑选10名志愿者进行兴趣变化测试，实验结果表明本文算法能够较为准确地反映用户兴趣的动态变化。

1 用户兴趣提取

用户在进行网页浏览时会留下用户的诸多信息，如果登录用户则会保留用户的个人信息以及对应的网页浏览记录，如果非登录用户则可以通过IP地址来标识该用户的浏览记录。在用户兴趣的提取时，我们可获得4类常用的信息（通称为浏览历史）：历史、书签、页面内容和访问日志。 浏览器通常会保持用户当前和以往会话中的请求记录。全局历史存储了访问页面的标题，URL，最初访问时间戳，最近访问时间戳，截止时间戳，URL访问的次数。通过浏览历史记录可以初步认定访问频率高的网页（即 URL）代表用户的较高兴趣。书签服务提供了用户对感兴趣的站点的快速访问，用户通常将自身经常需要访问或者感兴趣的网页内容以书签的形式加以存储，其中的 URL可认为是用户很感兴趣的内容站点。每个页面通常包含多个指向其他站点的链接，如果这个页面内容是用户感兴趣的，则他将很有可能会访问此页面所包含的链接，这一规则在搜索引擎领域也同样适用，经典页面排序算法则是参照此规则。因此，可认为访问页面包含的链接的可能性越大则用户对页面越感兴趣。对于索引页面，这点是非常重要的，因为，它包含了很多相关内容的链接，所以，相对于包含内容的页面，用户的浏览时间就很短。

本文通过搭建一个简易的页面浏览网站来提取用户的兴趣点，通过用户对网页的浏览历史，将浏览日志进行抽取分析，通过以上的4种指标对用户的页面停留时间来反映用户的每个网页具体的感兴趣程度。

2 用户兴趣表示

用户的兴趣呈现出多元化，用户可能同时对多个领域存在兴趣[4]，在细分到具体领域时，本文对用户的兴趣定义一个权值，称之为兴趣值，用兴趣值的高低来表示用户对各个领域的喜好程度。假设用户的兴趣维度以C表示，C={互联网、电影、音乐、美食、旅游}。各个领域对应的兴趣值如表1所示：

表1 兴趣值表示表

在表1中，用户的互联网兴趣值为0.32，电影兴趣值是0.14，可见用户对于互联网更具有兴趣。将用户的兴趣维度对应于向量中各个坐标系，各个兴趣维度的兴趣值对应于坐标系上坐标。则用户兴趣的表示如图1所示：

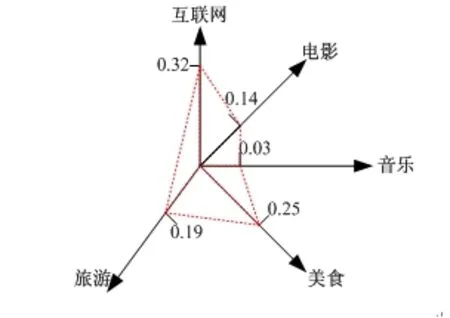
图1 用户兴趣表示

在图1中，将用户兴趣通过兴趣值加以量化，图中闭合红色部分表示用户的兴趣图谱。用户的兴趣非常抽象，用户兴趣值的量化也相对困难。本文以用户的浏览行为来表征用户兴趣值，通过用户在页面的停留时间在整个浏览时间的比重来表示兴趣值[5]。兴趣收集系统后台通过网页分类技术对网页进行分类，分类后的结果可以定义为各个兴趣领域，用户在固定时间段内的页面浏览会对应相应的兴趣领域。用户兴趣值的量化表示如公式（1）：

在公式（1）中，N表示网页分类后类别数目即兴趣领域的数目，表示用户在某个兴趣领域的页面停留时间之和，表示用户整个页面浏览时间总和。

3 用户兴趣动态变化

用户兴趣呈现一种动态的非规则变化，随着时间的推移用户的兴趣也会随之漂移，兴趣漂移呈现一定程度的不规则性，相对而言，用户新产生的兴趣领域应当相应地分配较高的兴趣值，因为用户可能受到当前环境和其他用户的影响。用户兴趣动态更新算法如表2所示：

表2 用户兴趣动态更新算法流程表

在表2中，用户的兴趣会随着时间的变化呈现非规则变化，对于每次捕获的用户兴趣列表，首先，需要判断用户的兴趣是否在当前的用户兴趣图谱中出现，如果出现则更新当前兴趣图谱中该兴趣的兴趣值，否则将新的兴趣加入兴趣图谱中。当完成用户兴趣列表的扫描后，则需要对用户的兴趣图谱进行全局更新，剔除用户历史兴趣中兴趣值低于阈值的兴趣[6]。

同时用户的兴趣也会随着时间的延展呈现一定程度的衰减，兴趣的衰减呈现逐渐递减的趋势，通过对大量用户行为日志的分析，用户的兴趣衰减近似呈现指数分布趋势，如图2所示：

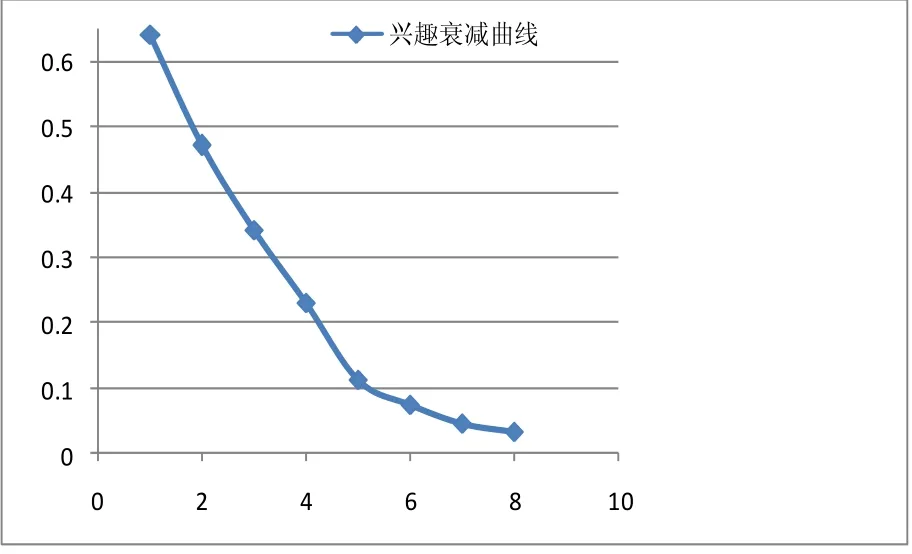
图2 兴趣衰减曲线图

将用户兴趣的衰减变化以公式加以量化，如公式（2）：

在公式（2）中，Δt为时间差，表示当前时间和历史时间之间的差值，v'表示经过衰减之后的兴趣值。

4 实验

实验选取10名志愿者对本文的算法进行验证。以新浪网作为兴趣采集资源点，采用Heritrix网络爬虫工具，以3天为周期，定期去爬取新浪门户网中网页，将爬取到的网页构建一个小型的本地浏览网站。挑选的10名志愿者根据自身兴趣选择从新浪门户网中爬取的内容网页进行浏览。分别采用基于单一兴趣的用户兴趣模型算法（算法 1）、基于多个兴趣的固定用户兴趣模型算法（算法2）和本文算法（算法 3），分别每种算法对用户兴趣变化之后的敏感度，通过比较3种算法在用户兴趣捕获上的准确率。

在表2中，α=0.01，将兴趣采集的资源采集周期定为10次，每次资源完成后，10名志愿者进行资源选择浏览。前 3周期的用户浏览行为定义为对用户兴趣图谱的补充和完整，随机挑选10名志愿者中一名，分别比较在3种算法下兴趣点的变化如表3所示：

表3 前三个周期下三种算法用户兴趣变化表

将后 7个周期采集的数据作为用户浏览行为的落地资源，用以对本文算法进行验证，分别比较3种算法对用户兴趣定为的准确率，如表4所示：

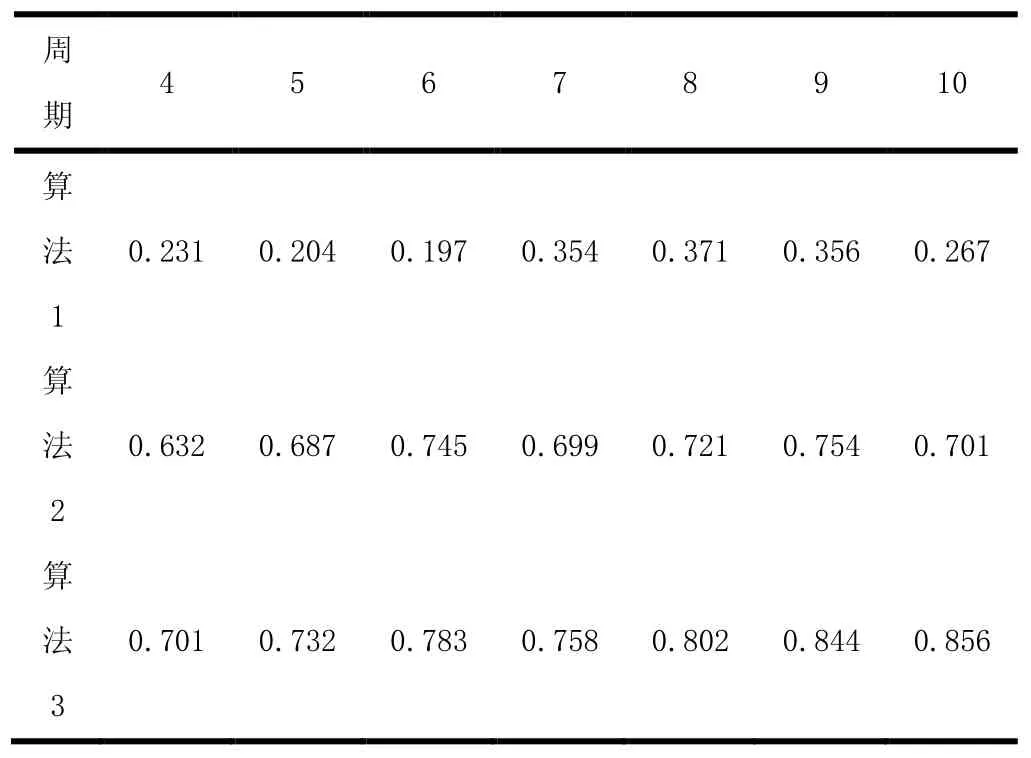
表4 三种算法在后七周期下用户兴趣捕获准确率表

3种算法在后7周期用户兴趣捕获准确率如图3所示：

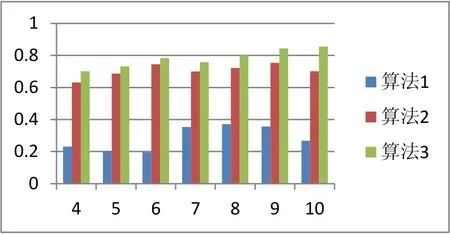
图3 三种算法在后7个周期用户兴趣捕获准确率图

在图3中可以看出，算法1（基于单一兴趣的用户兴趣模型）效果要低于算法2和算法3，并且算法2和算法3保持了相对较高的用户兴趣捕获准确率，算法2和算法3相比，算法3对用户兴趣变化的捕获更为敏感，由于是采用动态的对用户兴趣值进行调整并且实时的对用户兴趣图谱进行全局更新，因此能够保持较高的用户兴趣捕获准确率。同样在图3也可以看出，随着周期的延长，算法3的准确率性能也逐渐与算法2拉大，可见基于本文的算法能够较为准确并且敏感的判断用户兴趣的变化并能够实时反馈。

5 总结

本文以用户兴趣的表示为出发点，将用户的兴趣以多维尺度向量的方式加以表示，每个兴趣对应多维向量中一个坐标系，该兴趣的兴趣值对应坐标系中坐标值，通过这种方式来表示用户的兴趣图谱。用户的兴趣随着时间呈现出非规则变化，通过用户兴趣的变化动态的更新兴趣图谱，最后，挑选10名志愿者分别就本文算法和其它两种算法在兴趣表示准确度的对比，实验结果表明，本文算法能够比较准确地反映用户兴趣的变化。

[1]王永贵,张旭,任俊阳,等.结合微博关注特性UF_AT模型用户兴趣挖掘研究[J]. 计算机应用研究,2015,7.

[2]詹天晟,陈德华,乐嘉锦,等. 基于海量搜索历史数据的用户兴趣模型[J].计算机应用,2014,S2:126-129,139.

[3]史宝明,贺元香,张永. 个性化信息检索中用户兴趣建模与更新研究[J].计算机应用与软件,2014,03:7-10.

[4]于洪涛,崔瑞飞,董芹芹.基于遗忘曲线的微博用户兴趣模型[J].计算机工程与设计,2014,10:3367-3372,3379.

[5]任保宁,梁永全,赵建立,廉文娟,李玉军. 基于多维度权重动态更新的用户兴趣模型[J]. 计算机工程,2014,09:42-45.

[6]陶永才,何宗真,石磊,卫琳,曹仰杰. 基于加权动态兴趣度的微博个性化推荐[J]. 计算机应用,2014,12:3491-3496.

Research on User Interest Model Building Based on Multi-dimensional Vector

Wang Qingfu
(Liaoning School of Administration, Shenyang 110161, China)

The construction of user's interest model has been widely applied in personalized platform. Service customization according to users' interest has vital significance. A novel way of multi-dimensional vectoris proposed to reflect user’s interest, which could reflect the user’s interest feature better. At the same time, the user's interest will change irregularly with time; what’s more, the multi-dimensional vectorcould reflect this kind of irregular change through coordinate of each dimension. The experimental result on sina resource with ten volunteersshows that the proposed algorithm could reflect the change of user’s interest accurately.

Multi-dimensional Vector; User Interest; Dynamic-irregular; Interest Model

TP391

A

2015.03.09）

1007-757X(2015)05-0039-03

王庆福（1979-），男（汉族），辽宁盘锦人，辽宁行政学院，讲师，本科，研究方向：网络信息平台的设计，沈阳，110161