城市地下道路车速特征及运行车速模型

刘 硕，王俊骅，张兰芳，方守恩

（同济大学 道路与交通工程教育部重点实验室，上海201804）

随着我国城市化进程的加快，汽车保有量和出行量的增加，城市交通需求和供应之间的矛盾日益突出.地面空间资源的有限性和宝贵性促进了探索利用地下空间资源来解决城市交通的发展，增加城市交通的供给.面对国内愈发严重的城市交通拥堵问题，交通工作者在北京、上海、杭州等大城市进行了大量的地下道路规划及建设.地下道路是指地表以下供机动车通行为主的城市道路[1].目前，地下道路的规划设计大都参照城市地面道路或公路隧道相关规范标准，对运行车速的研究也大多集中在地面道路和公路隧道上.大量研究表明，平曲线半径是影响道路运行车速的最重要的指标，可以采用表征平曲线弯曲程度的特征指标（如曲线半径、曲率、曲线长度、偏角等）建立曲线路段各特征点（起点、中点和终点）的运行车速模型[2].也有研究将平、纵线形结合，通过在平面线形要素的基础上加上坡度、竖曲线等要素进行多元回归建模[3].而城市道路中影响运行车速的因素较多，道路线形、交叉口、用地类型、交通设施、路侧景观、限速[4]等均会对城市道路中车辆的行驶速度造成影响.此外，也有不少学者针对公路隧道的车速分布特性及运行车速模型[5－6]开展了研究.

近年来，随着城市地下道路的快速发展，虽然已有学者对地下道路中的车速分布[7]、影响因素[8]以及与地上道路的差异[1]进行了探索，但仍鲜有专门针对地下道路运行车速预测模型的研究.城市地下道路具有特定的使用功能和特殊的交通环境，不能简单地将现有的地上道路及公路隧道建设的规范和经验套用在城市地下道路上.本文通过实车实验采集地下道路中车辆的行驶速度，研究建立地下道路运行车速预测模型，为完善基于运行速度的地下道路设计与评价方法体系奠定基础.

1 实车测速实验

本文的测速方式采用实车测速.实验车辆为地下道路中最常见的普通5座小客车，车身长约4.6 m，宽度约1.8 m、高约1.5 m，加减速性能良好.考虑到地下道路中GPS信号受遮挡，在车身外侧装载非接触式五轮测速装置.车速测量范围为0～250 km·h－1，可以精确到0.1 km·h－1，测速误差范围为±0.5%.根据不同的设计标准和限速，选取了上海市8条城市地下道路进行实车实验，相关信息见表1.由于城市地下道路日间交通量较大，且具有明显的高峰小时，为保证车辆能够自由行驶，实车驾驶实验避开了交通高峰小时，多选在午后、傍晚或凌晨进行.实验过程中路段的交通流基本处于自由流状态，路面状况均良好，且不受大型货车、非机动车及行人的干扰.此外，由于天气对地下道路车辆运行特征的影响相对较小，本文暂不考虑天气的影响，实车实验均选择在晴朗或多云的天气下进行.

表1 实车实验隧道信息Tab.1 Basic information of test tunnel

为满足实验观测数据的精度，对理想条件下行车特征观测的最小样本量进行估算，按n＝（σK／E）2计算[9].其中，n为控制精度的最小样本量；σ为估计样本的标准偏差，城市道路通常取σ＝7.7；K为置信度水平系数，一般取95%的置信度水平，即K＝1.96；E为观测允许误差，根据研究需求和五轮仪的测量精度，E取2.5 km·h－1.计算得最小样本量为40个.实验招募了26名驾驶人进行实车驾驶实验，各路段样本量最大68个，最小42个，满足最小样本量要求.

2 地下道路车速特征

车速是多种因素共同作用的结果，统计学原理表明当随机变量受到大量偶然因素的影响并且各因素单独作用相对均匀且相互独立时，随机变量近似服从正态分布.根据车速分布柱状图显示，车速的分布具有中间集中，两边分散的特点，因此适合采用有峰值的分布形式进行拟合.研究表明，在农村公路或高速公路上，车速通常呈正态分布；在城市道路或高速公路匝道入口处，车速比较集中，一般呈偏态分布[10].城市地下道路的道路环境、车辆结构及组成有很大的特殊性.以外滩隧道（小型车专用隧道）为例，对比城市地下道路出入口、分合流段、直线段及曲线路段的车速分布.由车速频数直方图及累计频率曲线（图1），并通过 K－S（Kolmogorov－Smirnov）检验，表明城市地下道路各断面的车速数据基本服从正态分布.

图1 城市地下道路断面车速频数直方图及累计频率曲线Fig.1 Frequency histograms and cumulative frequency of speed in underground road

车速的不断变化是道路环境、车辆间相互作用、交通控制等因素共同作用的结果[11].

（1）线形.线形是影响驾驶人车速选择的重要因素.图2是车辆在地下道路中行驶的连续车速变化图.随着道路线形的不断变化，车辆会处于加速与减速的循环交替状态.通常情况下，上坡、小半径曲线路段的车速要低于下坡、直线路段的车速.另外，当平、纵线形相同时，车道宽度的改变对车速也有显著的影响.将车道宽度分别3.5 m和3.0 m的龙耀路隧道和外滩隧道进行比较，如图3所示，平、纵线形一致，车道宽度越窄，车速越低.

（2）洞口、分合流.通常在洞口及分合流路段，由于道路及交通运行环境的变化，驾驶人会对车速进行相应的调整.

（3）交通控制因素.限速、限行、减速带、快慢分流等控制方式，一方面会对车辆的速度产生一定程度的限制；另一方面，合理的交通控制技术、良好的交通秩序能显著提高路段整体交通安全和通行水平.

（4）交通量.随着交通流密度的增大，车速会降低.当流量较小时，车辆处于自由流中，驾驶人能自由选择行车速度，按期望车速行驶[7].本文主要研究在自由流状态下，地下道路中小型客车的运行车速模型.经统计，混合型的地下道路中小客车比例超过90%，小客车专用型的地下道路中小客车的比例更高，且很少受慢行交通的影响.因此，本文建模过程中，暂不考虑交通量、交通组成对车速的影响.

3 运行车速模型

运行车速是道路路线设计中重要的控制参数.基于运行车速的设计方法适应了路线设计的发展趋势，能够弥补基于计算车速作为设计车速进行线形设计所带来的不足，以车辆的实际行驶速度作为路线几何要素的“设计速度”.对地下道路运行车速的定义如下：自由流交通状态下，且路面状况良好时，小型车辆在特征断面上第85位百分点的车速作为该断面的运行车速.车速是连续型的随机变量，为了建模需要，本文将其进行离散化，以特征断面的车速作为研究对象.通常车辆进入直线会有一个持续加速的过程.若直线段长度够长，车辆在直线中点附近达到稳定车速，直至车辆接近下一平曲线处开始减速，通常在曲线中点附近的车速最低.车辆在要驶离曲线进入直线段时开始加速，进入下一个阶段的循环.因此本文选取了4个特征点位的车速，分别建立城市地下道路直线段稳定车速，直线段终点、曲线段中点及曲线段终点的运行车速预测模型.

3.1 数据处理

（1）根据线形设计资料找出直缓点、曲线中点、缓直点的桩号，将桩号与五轮仪记录的里程及车速相关联，并对应每组车速数据中直线段部分和平曲线段部分.

（2）经统计，地下道路中通常车辆需要的加减速距离不超过130 m，出于一般性的考虑，剔除了长度小于130 m的线形路段，以保证车辆有足够的加减速空间，在路段中达到稳定的车速.挑选了156个有效的典型线形路段，其中曲线路段91个，直线段65个.如前所述，各路段采集的车速样本量均满足最小样本量的要求.

（3）将挑选出的各特征点段的车速分别进行统计.直线段的稳定车速取每个驾驶人在直线段的最高车速.为避免试验过程中由于前方车辆行驶缓慢或者突然变道造成对试验车辆驾驶人的影响，需要剔除个别异常数据.本文用样本标准偏差的2倍来剔除异常数据，该点位有效样本的车速不应小于平均车速超过两个标准偏差，即v≥v－－2s（v－为平均车速，s为样本偏差）.

（4）通过统计分析得到每一个特征点段第85百分位的车速值.结合道路线形设计资料，建立地下道路运行车速数据库，将运行车速值与道路线形条件一一对应.

3.2 建模方法及自变量

现有的运行车速模型，大多数是根据道路平曲线半径或坡度建立与车速关系的一元回归模型[12].而城市地下道路中驾驶人车速决策行为的影响因素很多.地下道路作为城市道路的组成部分，不同的类型、等级及功能，道路条件也不尽相同.运行车速模型中若仅包含平曲线半径一个变量，则模型的离散度会较高，精度较差，实用性低.因此，对地下道路而言，建立单一线形指标与车速的关系模型已不再适用，需要建立包含多个指标的多元回归模型，才能使预测模型更为准确，适用性更加广泛.本文采用多元逐步线性回归进行地下道路运行车速预测模型的建立.车辆行驶时，驾驶人总是根据前方道路交通环境进行判断决策，从而进行车速的调整.尽管运行车速是按断面（点）进行划分的，但断面前后的道路线形均会对断面上的运行车速造成影响.因此，在构建运行车速预测模型时不仅需要包含断面所在路段的线形指标，同时还应包含断面前方路段的线形指标.研究表明，根据驾驶人视觉特性和跟踪捕捉道路信息的需求，道路线形在驾驶人的视窗罩中存在一个视觉敏感区域，通常也称为“注视范围”[13].一般取3 s行程作为驾驶人在行驶过程中前方线形影响范围的下限，取1.2倍停车视距作为前方线形影响范围的上限.

运行车速预测模型候选自变量包括平、纵、横线形，限制车速等，如表2所示.可以看出，地下道路运行车速预测模型的建模过程属于多元回归分析问题.而多重共线性[14]是多元回归分时普遍存在的一个问题，当共线性趋势非常明显时，会对模型的拟合带来严重的影响.

表2 运行车速模型自变量Tab.2 Independent variables

经反复尝试将上述全部或部分候选自变量引入多元回归分析方法中进行建模.为消除自变量之间存在的多重共线性问题，并综合考虑拟合优度的要求，建模过程中进行了如下处理：

首先，由于在实际的地下道路线形设计中，为保证平面线形各要素之间的协调性，圆曲线长度、缓和曲线长度、半径、曲率、偏角、曲率变化率等各要素之间客观上会存在一定的比例关系和相关性，因此，选取曲率变化率（Ccr）作为表征平曲线半径、曲线长度、超高、转角的综合变量，计算公式为

式中：Δ 为平曲线转角，（°）；L为平曲线长度，m；Lc为圆曲线长度，m；Ls1，Ls1分别为第一缓和曲线和第二缓和曲线长度，m；r为圆曲线半径，m.

第二，目前国内地下道路的线形是按照设计车速理论进行设计的.每一个标准下的设计车速都会有与之相对应的线形指标的取值，这些指标的取值也存在一定的客观相关性.如设计车速越高，通常车道宽度越宽，侧向净宽越宽，净高越高.因此，本文选取车道宽度作为表征净高、侧向净宽、通道宽度的综合变量.从最终多元回归分析的结果来看，能有效消除运行车速模型各自变量之间存在的多重共线性问题.

3.3 运行车速模型

应用统计分析软件SPSS，采用逐步分析法进行多元线性回归分析，建立城市地下道路运行车速模型，模型结果如表3～4及图4～6所示.

表3 回归模型Tab.3 Regression model

表4 模型回归检验结果Tab.4 Regression test

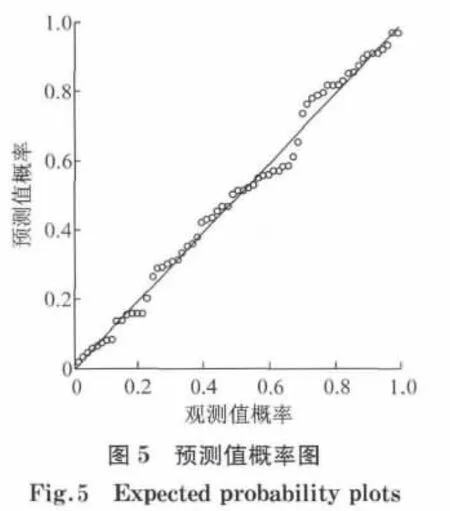
统计结果表明：①模型的拟合效果良好，且通过了残差齐次性分析及显著性检验.②车道宽度越宽、坡度越大（下坡为正，上坡为负）、曲率变化率越小，则运行车速越快.③在洞口路段，车速往往会有不同程度的降低.这是由于在隧道入口处存在“黑－白洞效应”，驾驶人视觉功能下降，需要通过降低车速来降低行车风险；而隧道出口路段，不仅存在“黑－白洞效应”，同时也往往存在纵坡较大的上坡，因此车速同样会降低.④车辆在分合流路段行驶时，驾驶人需要进行行车方向的选择，并受到其他车辆变换车道的影响，也会降低车速.尤其在直线路段，分合流对车速的影响更加显著.⑤路段终点处的车速不仅受当前路段线形的影响，还受前方路段线形的影响；前方路段为小半径曲线时，驾驶人往往会在进入小半径曲线前就开始减速.⑥限速、车道数、竖曲线半径等变量对于运行的车速影响很小，在逐步回归后没有进入最终的模型中.目前为确保行车安全，地下道路的限速通常会采用40 km·h－1或60 km·h－1，而不是采用设计车速.然而由于地下道路中通常线形较好，环境单调，空间封闭，驾驶人对速度感知的参照物较少，因此，超速现象频发[1].图7显示了各个限速下，地下道路车辆平均的超速值.从图7可以看出，地下道路中超速现象严重，限速越低，超速越明显，从一定程度上反映了驾驶人在城市地下道路中行驶时，主要是依据道路线形进行车速的选择，而不是根据限速进行调整的，因此，限速对运行车速模型的影响较小.目前，地下道路中追尾事故很大程度是由于超速引起的.设置合理的限速值、完善交通管控措施，是提高地下道路行车安全的重要途径.车道数、竖曲线半径未进入最终的模型，一方面由于建设成本、盾构机尺寸的限制，现有城市地下道路多为2车道（单洞）隧道；另一方面，地下道路在竖向上受限情况较少，竖曲线半径往往取值较大，不同类型的样本较少.因此，车道数、竖曲线半径没进入最终模型，其对于车速的影响有待进一步地研究.

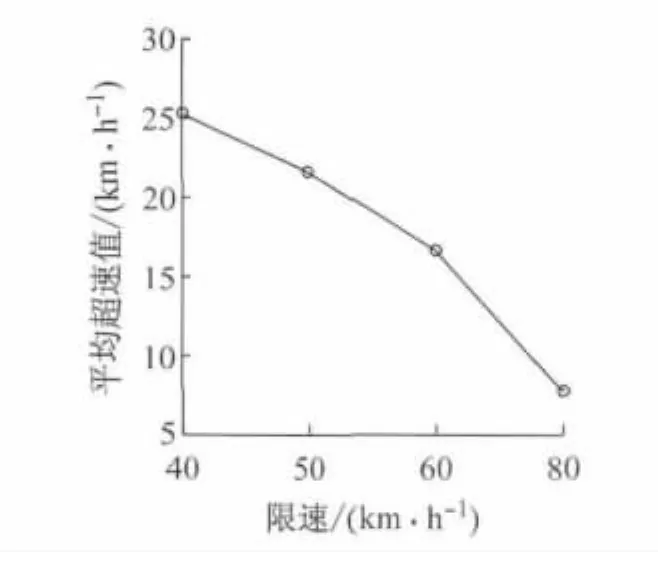
图7 地下道路超速情况Fig.7 Over speed in underground road

3.4 运行车速模型有效性验证

选取上海市迎宾三路隧道作为有效性验证对象.根据上述建立的车速预测模型计算运行车速，将预测值与实际测量值以及视频测量值进行比较分析，验证运行车速预测模型在实际工程应用中的有效性.

由图8可知，预测值与测量值的变化趋势较为一致，大多数预测值都与测量值较为接近，偏差较小.除隧道出口等个别情况下偏差稍大，实车测量值与预测值的偏差基本都在8 km·h－1以内，相对偏差小于10%.可以看出，运行车速预测模型具有较高的有效性和科学性.

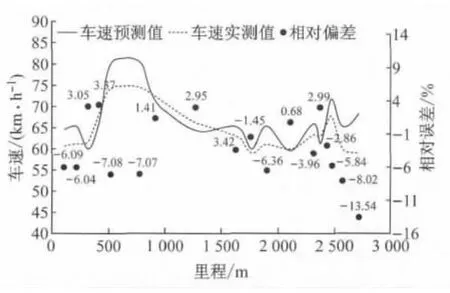
图8 城市地下道路车速预测值和实测值对比图Fig.8 Com parison of predicted values and measured values

4 结语

本文关于运行车速预测模型的研究建立在实测数据的基础上.实测路段包括多条上海市城市地下道路，设计车速为40，50，60，80 km·h－1的双向4～8车道的地下道路.根据模型有效性的检验结果，运行车速预测模型适用于设计车速在40～80 km·h－1的城市地下道路.实验数据表明，设计车速较低、线形指标较差的地下道路，车速变化较为明显；而设计车速为80 km·h－1的地下道路，线形指标通常较好，车速变化较小.目前的模型均采用线性回归的方法，实验路段均为上海市地下道路，并考虑到样本量的局限以及影响因素的组合类型不同，预测模型的有效性以及广泛适用性需要进一步完善.随着地下道路的快速发展，将会形成网络式的多进口多出口的地下道路系统，存在不同的匝道密度，也会出现设计指标更高，设计车速更快的地下道路，对其运行车速的准确预测也会变得更加迫切.

[1] 郑仕文.地下快速路车辆运行特征分析及其基于视觉计算的机理解析[D].上海：同济大学，2011.ZHENG Shiwen.Underground expressway vehicles running characteristics study and analysis of mechanism based on visual computing[D].Shanghai：Tongji University，2011.

[2] Krammes R A.Interactive highway safety design model：design consistency[J].Public Roads，1997，61（2）：47.

[3] Fitzpatrick K，Collins J M.Speed－profile model for two－lane rural highways[J].Transportation Research Record：Journal of the Transportation Research Board，2000，1737（6）：42.

[4] WANG Jun.Operating speed models for low speed urban environments based on in－vehicle GPS data[D].Atlanta：Georgia Institute of Technology，2006.

[5] 方靖，汪双杰，祝站东，等.高速公路隧道路段大型车运行速度模型[J].交通运输工程学报，2010，3：90.FANG Jing，WANG Shuangjie，ZHU Zhandong，et al.Operating speed models for trucks at expressway tunnel sections[J].Journal of Traf fic and Transportation Engineering，2010，10（3）：90.

[6] 赵友功.高速公路隧道速度特性分析及安全策略研究[D].西安：长安大学，2010.ZHAO Yougong.Analysis of speed characteristics and study on safety strategies of freeway tunnel[D].Xi’an：Changan University，2010.

[7] 李素艳，杨东援，刘艺.地下道路理论通行能力研究[J].地下空间与工程学报，2006，7（2）：1240.LI Suyan，YANG Dongyuan，LIU Yi.Research on basic capacity for urban tunnel[J].Chinese Journal of Underground Space and Engineering，2006，7（2）：1240.

[8] 刘硕，王俊骅，方守恩.地下道路横断面对驾驶行为的影响[J].同济大学学报：自然科学版，2013，41（8）：1191.LIU Shuo，WANG Junhua，FANG Shouen.Effect of crosssectional design on driving behavior in urban underground road[J].Journal of Tongji University：Natural Science，2013，41（8）：1191.

[9] 任福田.新编交通工程学导论[M].北京：中国建筑工业出版社，2011.REN Futian.Traffic engineering introduction[M].Beijing：China Architecture ＆Building Press，2011.

[10] Fitzpatrick K，Elefteriadou L，Douglas W H，et al.Speed prediction for two lane rural highways[R].Washington D C：Federal Highway Administration，2000.

[11] Transportation Research Board.Highway capacity manual[R].Washington D C：Transportation Research Board，2000.

[12] 高建平.高速公路运营安全性评价与对策研究[D].上海：同济大学，2006.GAO Jianping.The evaluation and countermeasures of expressway safety[D].Shanghai：Tongji University，2011.

[13] 阎莹，袁华智，蹇小平.高速公路线形三维空间综合指标与运行车速的关系模型[J].公路交通科技，2011，28（10）：102.YAN Ying，YUAN Huazhi，JIAN Xiaoping. Model of relation of expressway alignment 3D space comprehensive indexes with driving speed[J].Highway Traffic Science and Technology，2011，28（10）：102.

[14] 鲁茂.几种处理多重共线性方法的比较研究[J].统计与决策，2007，241（7）：8.LU Mao.Research on some treatment methods for measurement of multi－collinearity[J].Statistics and Decision，2007，241（7）：8.