针对结构易损场景监测的传感器优化布置方法

杨 伟，孙利民

（同济大学 土木工程防灾国家重点实验室，上海200092）

自20世纪后期以来，人们对桥梁结构的安全性、耐久性以及正常使用功能日益重视.为了保证桥梁结构在几十年、甚至上百年的服役期内能够安全、可靠地运营，越来越多的桥梁健康监测系统被安装在已建或新建的桥梁上.桥梁健康监测系统的主要功能是通过获取的激励和响应信号，对结构健康状况做出诊断和评估并对结构的异常反应做出预警，为桥梁的管理养护决策提供支持[1].近年来，虽然结构健康监测技术的研究与应用正变得逐步成熟，但是目前已建成的结构健康监测系统仍有许多不足之处.由于现有的监测技术和经费的限制，要监测与结构性能退化及结构安全性相关的所有重要部位往往是不可能的.如果监测部位和传感器布置位置没有经过慎重的选择，获取到的信息就不能有效地反映结构的健康状况.因此，如何以有限的测点尽量多地获取与结构性能退化及安全性相关的信息是健康监测系统研究中的一个难点.

传感器布置问题在航空航天、机械、土木以及交通等领域得到广泛研究，成果十分丰富.其中，以基于Fisher信息矩阵的结构参数估计误差最小为原则进行传感器布置是最为常用的布置方法之一[2－4]，另外，Guyan模型缩减法[5－6]以及基于模态应变能的方法[7]也是常用的传感器布置方法.以上方法均是以增加系统可观性或系统可控性为目标进行传感器布置，通过这些测点获取的结构信息不能很好地反映结构的损伤状况，因此，一些学者[8－10]提出了以结构损伤识别为目的的传感器优化布置方法.他们希望找到一组测点，在使用这些测点输出的测试数据进行损伤识别时，识别误差最小.然而，试图用有限的监测资源提高所有构件的损伤识别精度往往是不明智的，并不是所有构件的损伤都会对结构性能造成严重的影响并且最终导致结构失效.本文主要研究如何将有限的监测资源配置在更合理的位置，使获取到的结构信息能最有效地反映结构性能受损伤的影响.

在对传感器的布置位置进行优化时，考虑到结构对不同损伤场景的易损性是不相同的，在对结构各损伤场景的易损性作定量分析后[11－12]，定义了一个基于易损性指数的结构失效指标.在Kammer[2]和Shi等[9]的研究基础上，利用该评价指标，提出了一种以监测结构易损场景为目的的传感器优化布置方法.最后以一个平面桁架结构为研究对象，利用该方法对其进行传感器布置，并且与两种传统方法进行比较，验证了本文方法的可行性及有效性.

1 传感器优化布置方法的理论基础

1.1 基于结构易损性分析的失效指标

对于一个结构，如果微小的损伤造成了不成比例的破坏后果，则称此结构是易损的[11].为了清楚说明结构易损性的量化评价方法，首先引入如下基本概念：损伤场景D，指结构在一个破坏事件中发生损伤的构件集合；易损场景V，指易损性较高的损伤场景，若一个损伤场景是易损场景，用符号D∈V表示；结构失效，指损伤造成结构性能下降至结构设计性能需求值之下的结构状态.

结构损伤可以用受损伤的单元刚度矩阵乘以损伤系数α来表示.αi∈ [0，1]代表i号单元的损伤系数，0表示无损伤，1表示单元刚度退化为零，单元完全失效；αDi称为损伤场景Di的损伤系数，为了便于易损性的定量计算，假设损伤场景所包含的所有单元的损伤系数都为αDi.用表示损伤场景的容许损伤系数，P表示结构设计性能表示结构设计性能需求值，则损伤场景Di的容许损伤系数可表示为

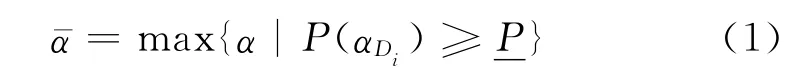
在给定的下，结构容许损伤系数α¯将会随着不同的损伤场景而变化.当α¯＝1时，该损伤场景不会导致结构失效；当＜1时，表示该损伤场景发生后，随着损伤程度的加深，结构性能将逐渐下降至性能需求值以下，结构体系最终将失效.

易损性指数I是用来定量衡量结构易损程度的指标，它表示结构的破坏后果与破坏需求之比[13].结构破坏后果指损伤场景发生所造成的结构性能下降；破坏需求是使结构损伤发生所需作用的测度，可以用受损构件的弹性模量折减来表示.从该定义可以看出，易损性指数越高，结构破坏后果与初始损伤越不成比例，结构越易损.由于易损场景是易损性较高的损伤场景，本文将可能导致结构失效的损伤场景称为易损场景，即＜1的损伤场景为易损场景.损伤场景Di的易损性指数可表示为

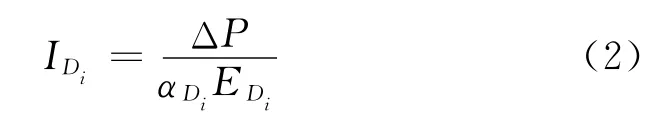
式中：αDi为损伤场景Di的损伤系数；EDi为损伤场景包含的构件弹性模量之和；αDiEDi为损伤造成的弹性模量折减，用来表示破坏需求；ΔP为损伤造成结构性能的下降值，用来表示结构破坏后果.对于所有的易损场景，若损伤系数为容许损伤系数Di，则结构性能的下降值都为ΔP＝P－.因此可使用相对易损性指数IV＝1／DiEDi）作为判断易损场景易损性大小的指标.

借助损伤场景的易损性指数以及损伤系数的概念，定义一个判断损伤场景D发生后，结构是否失效的评价指标S.

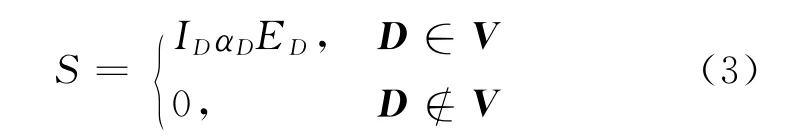
式中：向量V＝（V1，V2，…，VN）T包含该结构所有可能出现的易损场景.

结构失效指标S∈ [0，＋∞）是一个量纲为一的常数，当S＝0时，表示该损伤场景不会导致结构失效；当0＜S＜1时，表示结构还未失效，但损伤系数αD继续增大将导致结构失效；当S≥1时，表示该结构已经失效.该指标与结构安全性密切相关，健康监测系统可以根据该指标对受损结构的失效状态作出有效评估并根据评估结果及时作出预警.

1.2 传感器优化布置模型

结构健康监测系统获取到的模态参数往往具有不确定性，这种不确定性通常来源于有限元模型与实际结构的误差、监测环境的不确定性以及监测数据中的噪声输入这三方面.对模态参数不确定性的研究表明[14]，模态参数的概率分布可以很好地近似为高斯分布模型.由于健康监测系统根据模态参数对结构损伤进行识别，模态参数的不确定性将导致结构失效指标S的计算值与真实值之间存在误差，影响健康监测系统对结构安全状况评估的可靠性.因此，本文希望通过传感器的优化布置，在模态参数不确定性无法避免的情况下，尽量减小结构失效指标S的估计误差，提高对结构健康状况评估的可靠性.

对于一个n自由度的受损结构，假设结构阻尼可以忽略并且损伤只引起结构的刚度变化，而不影响结构的质量分布.结构的测试模态振型向量为｛｝∈Rkn×1，k为模态阶数，A为结构体系的损伤系数，Α＝｛α1，α2，…，αL｝T，其中，L为可能会发生损伤的单元总数.它们之间的函数关系可以简单表示为

如果考虑模态参数的不确定性，则式（4）变为

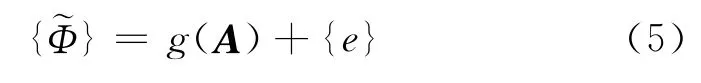
式中：｛e｝表示获取到的测试模态振型与真实模态振型之间的误差，服从均值为0，方差为σ2的高斯分布，并且假设各自由度的误差相互独立.

测试模态振型向量与结构损伤系数之间是复杂的非线性关系，无法直接对损伤系数进行求解.在实际损伤识别过程中，通常先将式（5）展开为泰勒级数表示的线性关系式，再迭代求解出损伤系数.式（5）可以线性近似表示为

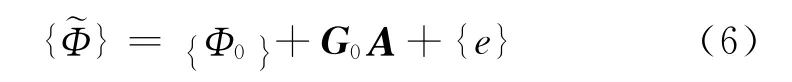
当用测试模态振型向量对结构损伤系数Α做无偏估计时，其估计量的协方差矩阵满足以下不等式：

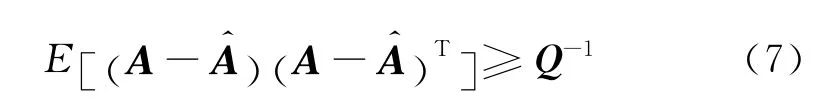
方差达到Cramer－Rao下界的无偏估计称为有效无偏估计，已知最小二乘估计LS是一种有效无偏估计[16].因此Α的最小二乘估计量的协方差矩阵等于Cramer－Rao下界.Α的最小二乘估计量为

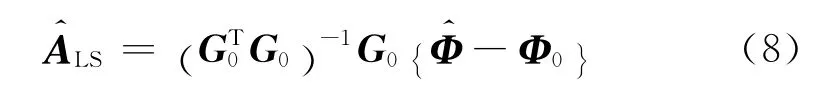
式中：Q－1∈RL×L，其对角线上每一个元素Q－1（i，i）分别为LS中每一个元素LS（i）的方差.

由线性参数估计理论[16]可知，最小二乘估计量LS是测试模态振型向量｛｝的线性组合，在｛e｝服从高斯分布的假设下，｛｝服从高斯分布，则LS也服从高斯分布，因此

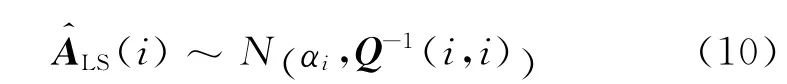
假设某一易损场景包含M个受损构件，并且所有受损构件的损伤系数都为αV，则该易损场景结构损伤系数的估计值可表示为

将公式（11）带入公式（3），得到某一易损场景发生后结构失效指标S的估计值为

由于为LS的线性组合，因此也服从高斯分布，并且由公式（10）中LS（i）的分布可以推导得到S＾的分布为

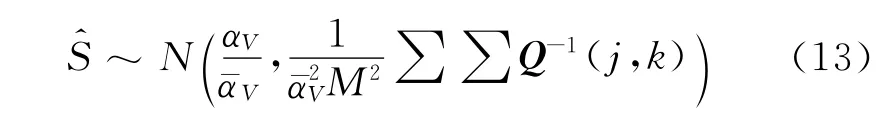
式中：j，k为易损场景V 所包含构件的编号，j，k∈V.

为了减小模态参数的不确定性对结构失效指标S计算精度的影响，需减小估计值的方差D（）.考虑所有可能发生的N个易损场景，需使方差和尽量减小.因此，本文传感器优化布置的本质是如何对模态数据进行选取，使方差和最小.

对于一个n自由度的结构，假设只可以在其中m个位置布设传感器，则对每一阶模态振型，这个选择的过程可以表达为

式中：C∈Rm×n是一个上三角的自由度选择矩阵，每一行只有一个元素不为0，且等于1，这个等于1的元素所在的列数即为选择出来的自由度，并且C中每一行等于1的元素所在的列数要大于前一行中这个元素所在的列数.将公式（14）带入公式（9），LS的协方差矩阵在自由度经过筛选后变为

式中：Z＝CTC，是一个n阶的对角阵，对角线上只有被选中的自由度所对应的元素为1，其余都等于0.并且，对角线上所有元素之和为布置的传感器数量m.

因此，与本文传感器优化布置问题等价的数学优化模型可写为

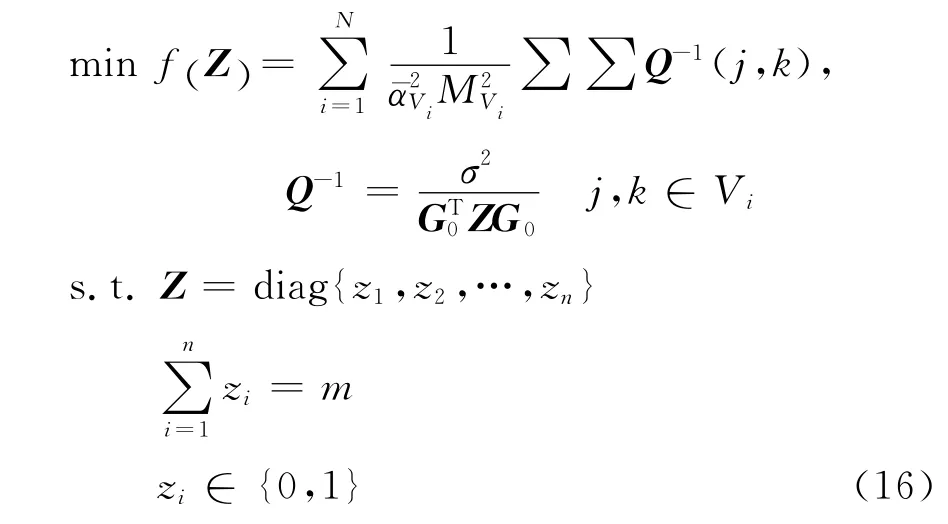
1.3 优化模型的求解

求解公式（16）所示的最优化模型最简单的方法就是尝试所有的个可选择的测点组合，然而这种遍历算法只有在结构自由度n较小时可行，结构自由度数目超过一定规模，计算量会非常庞大，使求解变得非常困难.本文基于凸规划方法选取了一种对该优化模型的近似求解方法[17]，可有效地求解此模型.

对目标函数f（Z）二次求导，可得到如下形式：

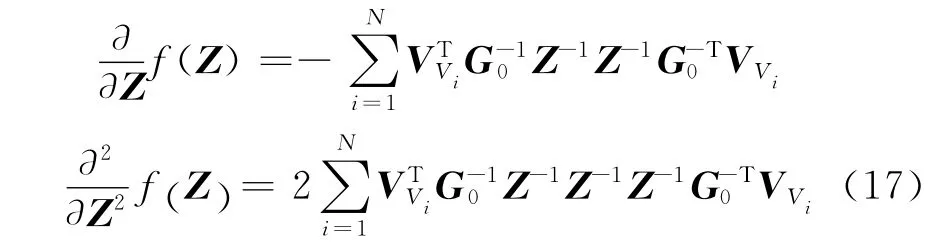
对于式中向量VVi∈RL×1中各元素，易损场景Vi包含的构件所对应的元素值为，其余均为0.

由公式（17）可见，目标函数的二阶导数为正定矩阵，则目标函数是一个凸函数，并且目标函数在可行域内大于0，因此该优化问题必定有最优解.然而由于该优化模型中的一个约束zi∈｛0，1｝是非线性的，使该优化问题难以直接采用基于凸规划的方法求解.将约束zi∈｛0，1｝松弛为zi∈ [0 ，1]后，得到了一个新的优化模型：

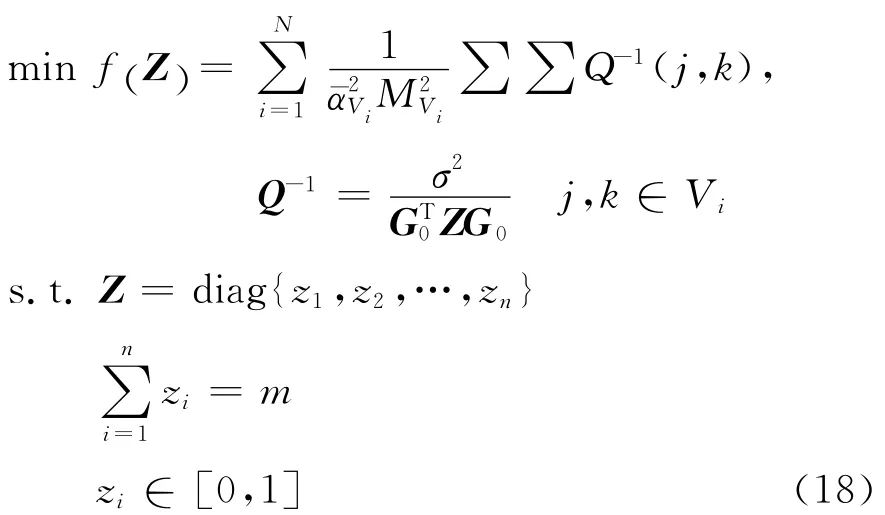
这个松弛后的优化模型是典型的凸优化问题，采用内点惩罚函数法[18]可以对其快速、有效地求解.

求得松弛解Z＊之后，对Z＊内各元素按从大到小的顺序重新排列得到则初步选出的自由度为前m个自由度

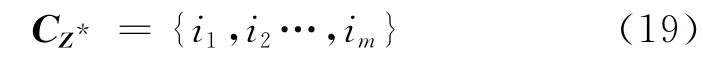
对该初步解进行局部优化可以得到更精确的结果.局部优化算法是从m个选中的自由度中依次选出一个自由度与n－m个未被选中的自由度交换，并且计算目标函数值，一旦得到更小的目标函数值，则交换后的m个自由度成为新的优化解CZ＊，并且重新开始局部优化.当m（n－m）次交换全部完成，并且没有出现更小的目标函数值时，算法结束.此时的优化解CZ即为最终选定的m个布置传感器的自由度.

图1为本文提出的针对结构易损场景监测的传感器优化布置方法流程图.

图1 传感器优化布置流程图Fig.1 Flowchart for optimal sensor placement

2 算例

算例采用文献[12]中的一个平面桁架结构，其几何模型及构件编号如图2所示.该结构的有限元模型由29个二维杆单元组成，构件编号为①～○29，节点数为15，每个节点有x和y方向两个自由度，除去被约束的4个自由度，可布置传感器的自由度数为26.

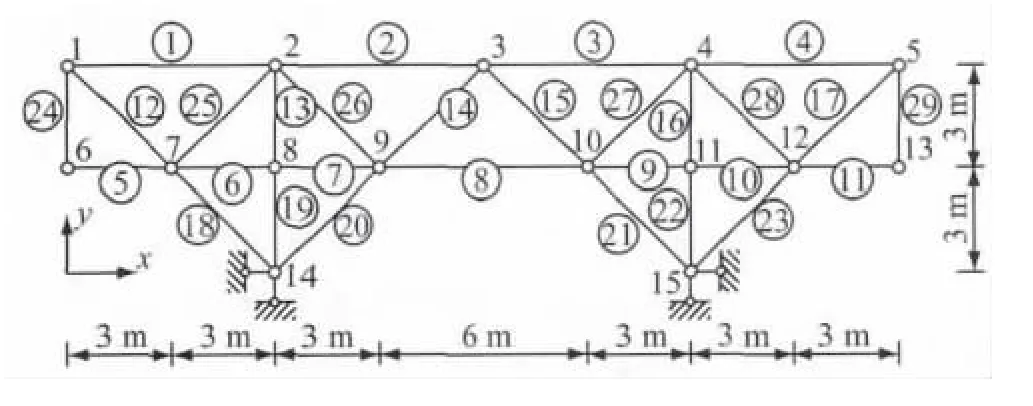
图2 平面桁架结构模型Fig.2 Structural model of a plane truss

结构承受的荷载形式不同，则构件承载能力的发挥程度不同，通常结构易损性分析结果受荷载形式影响很大.在对该算例结构进行易损性分析时，仅考虑结构受恒载情况，用图3所示的节点集中力模拟结构恒载.构件的材料和截面信息参考文献[12].

图3 结构荷载（单位：k N）Fig.3 Load condition（unit：k N）

文献[12]以图2所示的桁架结构为分析对象，在承受如图3所示的结构荷载情况下，将结构的极限荷载乘子作为结构的性能参数，利用机构生成法计算结构体系的极限荷载乘子以及相应的失效模式.分析根据极限荷载乘子随不同损伤场景的损伤系数的变化，得到结构在指定结构性能需求下不同损伤场景的容许损伤系数.最后根据容许损伤系数确定了结构可能出现的所有易损场景及相应的易损性指数，结果如表1所示.

该结构为左右对称结构，所考察的易损场景仅包括左半结构中的构件.由表1可见，对于所列出的各易损场景，按易损性大小由高到低依次为：①，㉔，⑱，⑲，⑳，⑫，㉕，⑭，㉖.

将易损性分析结果带入公式（18）所示的优化模型中进行计算，发现随着布置的传感器数量逐渐增多，目标函数的最优值不断减小.如图4所示，当传感器的数目超过10之后，最优值减小的速率变缓.因此，本文考虑从结构26个可选自由度中选出10个自由度进行传感器布置，并且在优化计算中考虑结构前10阶模态，得到针对结构易损场景监测的传感器布置方案如表2中方案1所示.

表1 结构易损性分析结果Tab.1 Results of structural vulnerability analysis

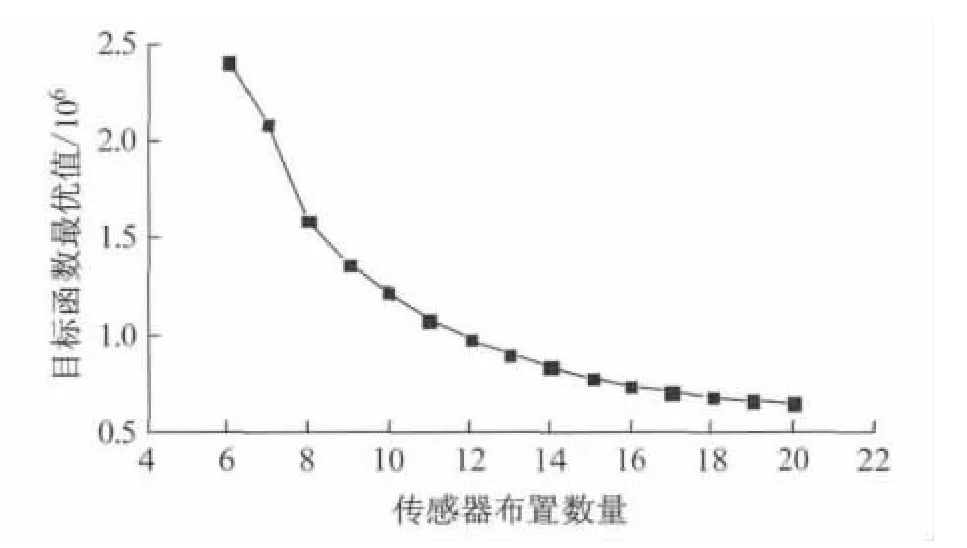
图4 随传感器布置数量变化的目标函数最优值Fig.4 Optimal objective value as a function of sensor count

另外，为了与本文所提出的传感器优化布置方法作比较，表2还给出了两种传统方法确定的传感器布置方案.表2中方案2根据Kammer[2]所提出的基于提高模态可观测性的有效独立法（EI法）确定；方案3根据Shi等[9]提出基于结构损伤可识别的传感器优化布置方法确定.

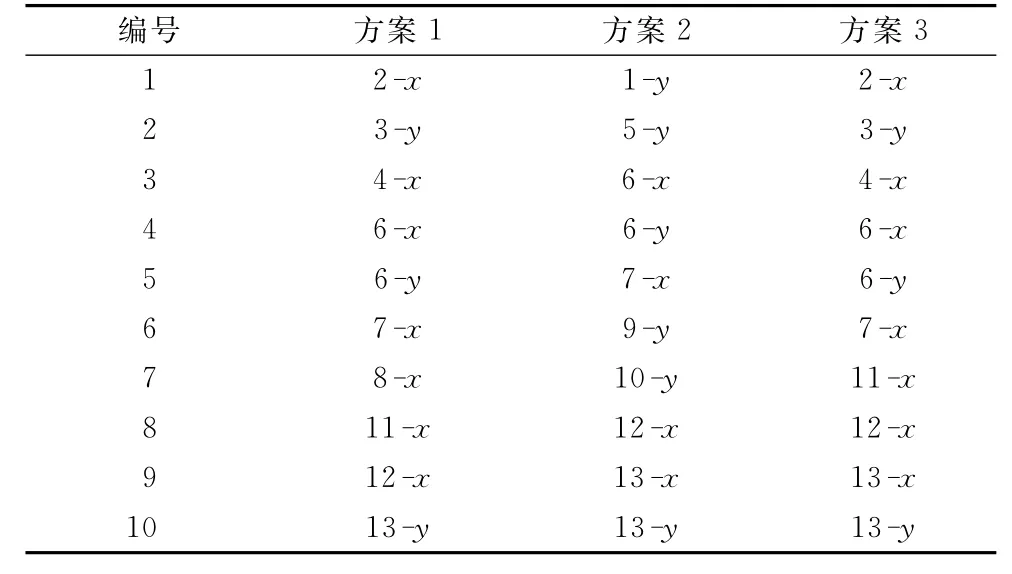
表2 3种传感器布置优化方案（节点－方向）Tab.2 Sensor locations for three different displacement methods

图5为3种传感器布置方案示意图.图中黑色三角的指向为所在节点需要布置传感器的自由度方向.

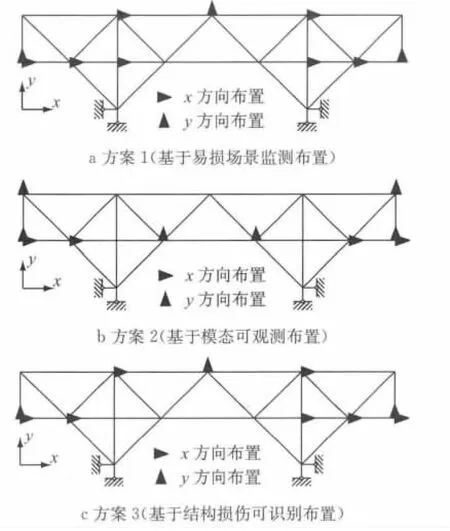
图5 3种传感器布置方案示意图Fig.5 Sensor locations for three different displacement methods

理论分析表明，针对结构易损场景监测的传感器布置方案相比传统的布置方案可以对结构失效状态作出更准确的评估.为了验证这一点，假设结构发生如表3所示的7种易损场景，分别使用3种传感器布置方案获取的模态信息计算在模态参数不确定性影响下的结构失效指标，通过比较指标的均值和方差来考察本文方法的有效性.

表3 结构易损场景Tab.3 Structural vulnerable scenarios

本文通过对模态振型人为添加高斯分布的随机误差来模拟模态参数的不确定性.随机误差可以表示为

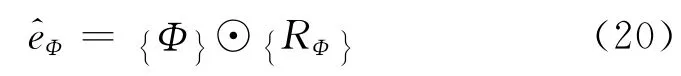
式中：｛Φ｝为有限元计算得到的模态振型向量；向量｛RΦ｝为误差比例系数，是一组相互独立均值为0的高斯分布随机数；符号⊙表示元素对应元素相乘.考虑数据不确定性的模态振型为

蒙特卡洛方法是一种非常强大的统计分析方法，经常被用来分析模态参数的不确定性对损伤识别结果的影响[19].这种方法的本质是使用大量添加过随机误差的数据样本来模拟高斯分布的真实模态参数.本文利用蒙特卡洛方法，模拟得到5 000组标准差为1%的误差比例系数向量，并带入公式（21），得到模拟的模态振型样本，并使用这些样本对结构进行损伤识别.

各组样本的损伤系数通过模型修正方法[20]识别，模型修正以样本与完好结构振型差值的平方和最小为目标函数迭代计算损伤系数.再根据识别的结果计算结构失效指标的均值E（）和方差D）.以易损场景7为例，蒙特卡洛方法模拟识别计算的过程如图6所示，可以看出，5 000组样本可以计算得到稳定的均值和方差.

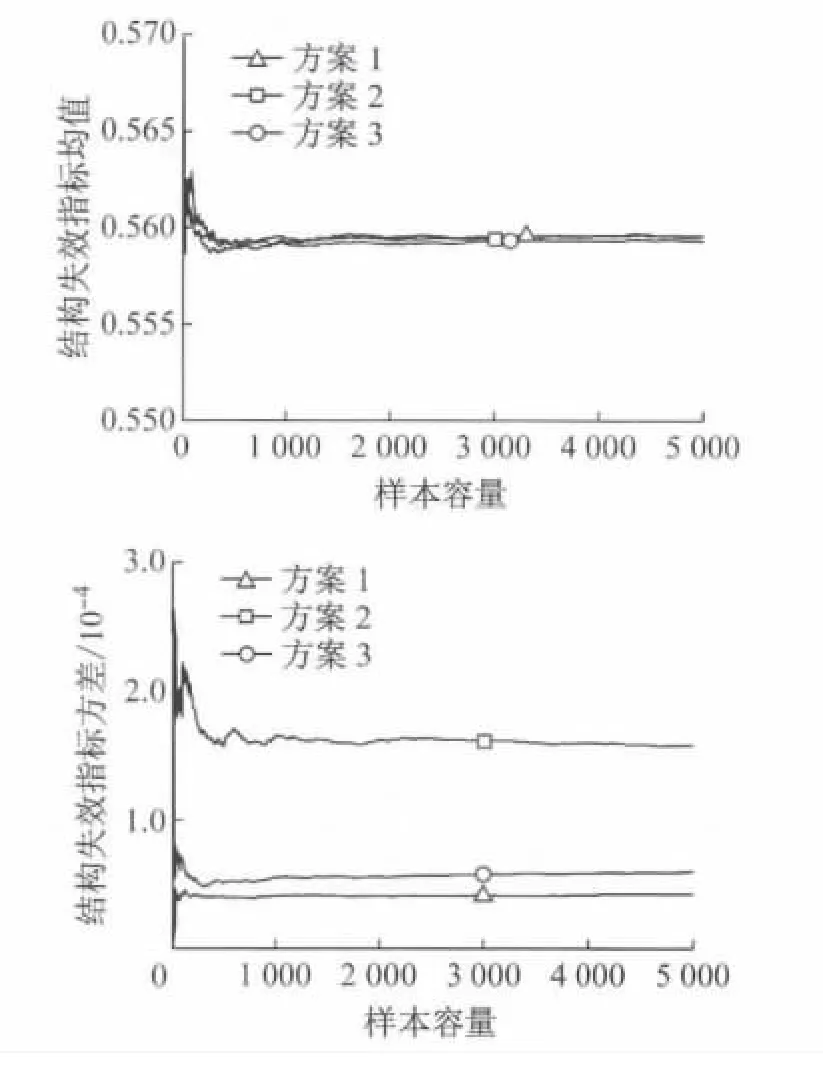
图6 蒙特卡洛方法模拟计算结构失效指标（易损场景7）Fig.6 Computation of structural failure index using Monte Carlo simulation

图7为所有易损场景的结构失效指标均值及方差的计算结果.由图7可以看出，对于该桁架结构可能出现的7种易损场景，3种传感器布置方案得到的结构失效指标的均值与真实值都非常接近；但本文方案得到的指标方差明显小于其他两种传统方案得到的方差.算例的结果可以验证理论分析所表明的，在模态参数不确定性的影响下，针对结构易损场景监测的传感器布置方案相比传统的传感器布置方案在对结构失效状态进行评估时可以得到更精确的结果.

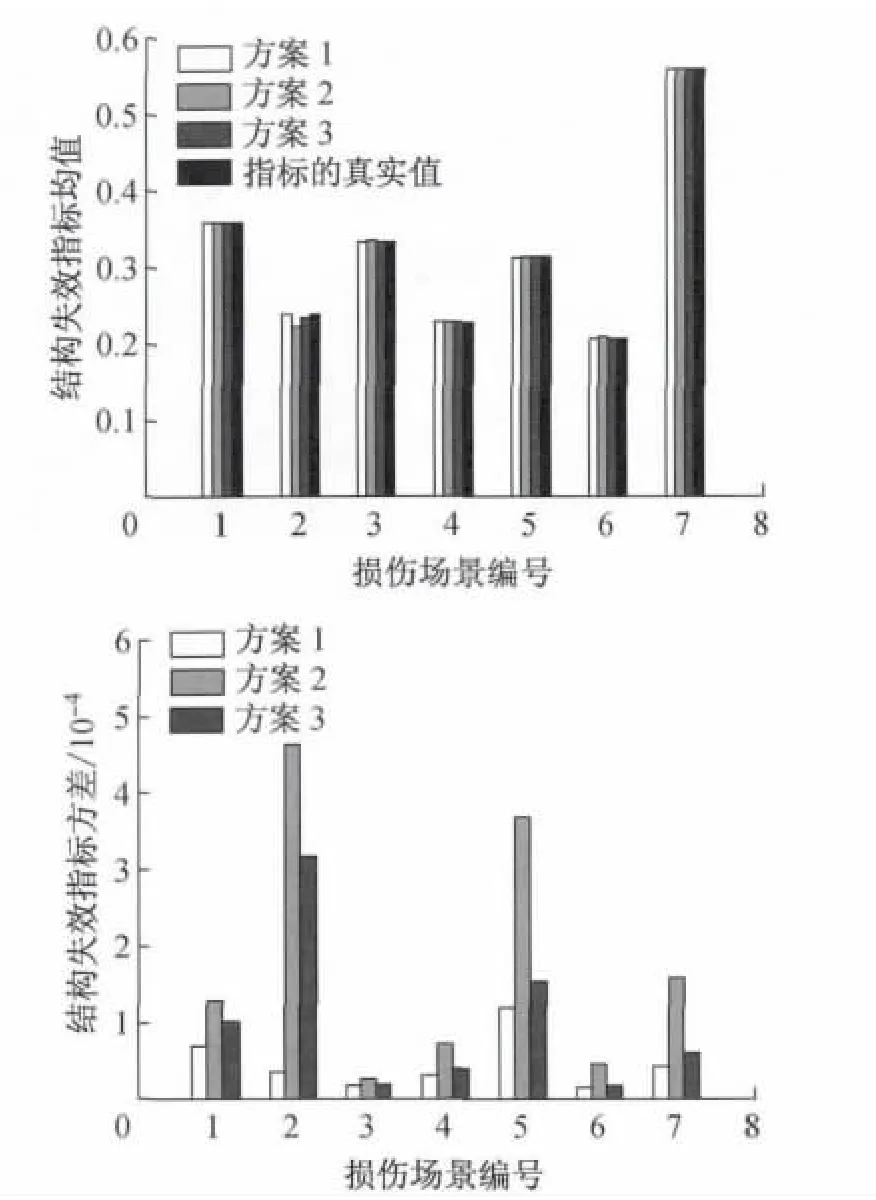
图7 3种布置方案的结构失效指标均值及方差计算结果Fig.7 Mean and variance results for three different sensor displacement methods

3 结论

（1）结构易损性建立了结构失效状态与结构损伤识别之间的关系.文中基于易损性指数和损伤系数定义的结构失效指标可以有效反应易损场景发生后结构的失效状态，健康监测系统可以根据该指标对结构安全状况作出有效评估以及针对异常情况及时作出预警.

（2）在传统传感器优化布置理论基础上，以所有易损场景下结构失效指标估计方差和最小为优化目标，提出了针对结构易损场景监测的传感器优化布置方法及相应的求解算法，算例验证了方法的可行性与有效性.结果表明，利用3种不同的优化方法布置传感器，计算得到的结构失效指标均值与真实值都非常接近，而本文方法得到的方差比两种传统方法得到的方差更小.

[1] 孙利民，孙智，淡丹辉，等.我国大跨度桥梁结构健康监测系统研究与应用现状 [C]∥第十七届全国桥梁学术会议论文集.北京：人民交通出版社，2006：663－670.SUN Limin，SUN Zhi，DAN Danhui，et al.Research and application of long span bridge health monitoring system in China [C]∥Proceedings of the 17th National Conference on Bridge.Beijing：China Communications Press，2006：663－670.

[2] Kammer D C. Sensor placement for on－orbit modal identification and correlation of large space structures [J].Journal of Guidance，Control，and Dynamics，1991，14（2）：251.

[3] Udwadia F E.Methodology for optimum sensor locations for parameter identification in dynamic systems [J].Journal of Engineering Mechanics，1994，120（2）：368.

[4] 秦仙蓉，张令弥.一种基于QR分解的逐步累积法传感器配置 [J].振动测试与诊断，2001，21（3）：168.QIN Xianrong，ZHANG Lingmi.Successive sensor placement for modal paring based－on QR－factorization [J].Journal of Vibration，Measurement ＆Diagnosis，2001，21（3）：168.

[5] Guyan R J.Reduction of stiffness and mass matrices[J].AIAA Journal，1965，3（2）：380.

[6] 谢强，薛松涛.结构健康监测传感器优化布置的混合算法[J].同济大学学报：自然科学版，2006，34（6）：726.XIE Qiang，XUE Songtao.A hybrid algorithm for optimal sensor placement of structural health monitoring[J].Journal of Tongji University：Natural Science，2006，34（6）：726.

[7] Heo G，Wang M，Satpathi D.Optimal transducer placement for health monitoring of long span bridge[J].Soil Dynamics and Earthquake Engineering，1997，16（7）：495.

[8] Cobb R G，Liebst B S.Sensor placement and structural damage identification from minimal sensor information [J].AIAA Journal，1997，35（2）：369.

[9] Shi Z，Law S，Zhang L.Optimum sensor placement for structural damage detection [J].Journal of Engineering Mechanics，2000，126（11）：1173.

[10] Zhou X Q，Xia Y，Hao H.Sensor placement for structural damage detection considering measurement uncertainties [J].Advances in Structural Engineering，2013，16（5）：899.

[11] 于刚.结构易损性分析及其在桥梁健康监测中的应用 [D].上海：同济大学，2009.YU Gang.Structural vulnerability analysis and its application on bridge health monitoring [D]. Shanghai： Tongji University，2009.

[12] 于刚，孙智，孙利民.基于塑性极限状态的结构易损性分析[J].哈尔滨工业大学学报，2011（12）：1953.YU Gang，SUN Zhi，SUN Limin.Structural vulnerability analysis based on plastic limit state [J].Journal of Harbin Institute of Technology，2011（12）：1953.

[13] England J，Agarwal J，Blockley D.The vulnerability of structures to unforeseen events[J].Computers ＆Structures，2008，86（10）：1042.

[14] Doebling S W，Farrar C R，Goodman R S.Effects of measurement statistics on the detection of damage in the Alamosa Canyon Bridge[C]∥Proceedings of the Proceedings－Spie the International Society for Optical Engineering.Citeseer：Society of Photo－optical Instrumentation Engineers，1997：919－929.

[15] Fox R，Kapoor M.Rates of change of eigenvalues and eigenvectors[J].AIAA Journal，1968，6（12）：2426.

[16] 张金槐.线性模型参数估计及其改进[M].北京：国防科技大学出版社，1992.ZHANG Jinhuai.Linear model parameter estimation and improvement[M].Beijing：National University of Defense Technology Press，1992.

[17] Joshi S，Boyd S.Sensor selection via convex optimization[J].Signal Processing，2009，57（2）：451.

[18] 陈宝林.最优化理论与算法[M].北京：清华大学出版社有限公司，2005.CHEN Baolin.Theory and algorithms of optimization[M].Beijing：Tsinghua University Press Co，Ltd，2005.

[19] Sanatei M，Saletnik M J.Parameter estimation of structures from static strain measurements.Ⅱ：error sensitivity analysis[J].Journal of Structural Engineering，1996，122（5）：563.

[20] Gorl E，Link M.Damage identification using changes of eigenfrequencies and mode shapes[J].Mechanical Systems and Signal Processing，2003，17（1）：103.