图式理论在平面向量复习中的应用

包道永

【摘要】平面向量的有效复习，可以帮助学生体会数学的内部联系、数学与实际生活的联系，以及数学在解决实际问题中的作用。将图式理论用于指导平面向量的复习，有助于激活和调动学生已具备的代数、几何、物理知识，有效地内化并成为学生的心理结构图式。

【关键词】平面向量 图式 数学模型

【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089（2015）04-0170-01

1.引言

2014年江苏高考数学的均分达到96分左右，命题保持了一贯的风格，以考查基础知识、基本技能和数学思维能力为主。试题仍然重视基础，考察了8个C级考点。解答题前三题，分别考察了三角函数、立体几何、解析几何，相对比较基础、容易上手，从考生反馈的情况看，大部分考生这三题都比较容易上手。

数学基本能力主要包括空间想象、抽象概括、推理论证、运算求解、数据处理这几方面的能力。向量是近代数学中重要和基本的数学概念之一，它是沟通代数、几何与三角函数的一种工具，有着极其丰富的实际背景。向量既是重要的数学模型，又是重要的物理模型。向量的引入，给高中数学教学带来了生机，也为今后学习高等数学奠定了必要的基础。因此，研究搞好平面向量的复习教学是有必要的，也是非常重要的。

本章要求学生掌握向量的线性运算和数量积的运算，这就把运算的对象从数、字母扩展到了向量。这为进一步理解其他的数学运算（如函数的运算、映射、变换、矩阵的运算等等）创造了条件，特别是当学生利用向量运算解决了数学中（如推导两角差的余弦公式）和物理中的问题时，就更有助于学生体会数学运算的意义，感悟运算、推理在探索和发现中的作用了（吴庆麟等，2002）。

2.理论综述

图式是大脑为了便于信息储存和处理，而将新事物与已有的知识和经历有机地组织起来的一种知识表徵形式。图式是陈述性知识的一种高水平的表达形式。它将一些低水平的陈述性知识单元如命题、表象及线性排序组织起来。Cook（1989，1994）认为，图式是头脑中的“先存知识”或“背景知识”。有学者将图式的特点“比作一个庞大的档案系统，它把个人的知识经验分门别类储存在大脑中，大脑接受一个新信息后，便会设立一个新的文件夹（或先验图式），或把新的信息输送到现存的先验图式之中”。

可见，研究“知识图式”在教与学中的作用，使学生更有效地把知识串联起来。图式的形成不仅能够给人的记忆提供支持，减轻记忆负担，还能使人迅速地识别属于某一范畴的新例证或事件，并依据这种最初的识别对遇到的新情况做出推论，从而简化人对事物的鉴定与分类（吴庆麟等，2002）。人们记忆中储存的这些图式还有助于问题解决。

3.图式理论在复习平面向量中的运用

人脑中保存的一切知识都能分成单元、构成“组块”和组成系统，这些单元、“组块”和系统就是图式。它的表征形式是命题、表象、线性排序等，是对一般概念的有意义信息形成的一个集合体。这里的一般概念可以是客体的类目，数学中的三角形、等比数列、二次函数等；也可以是一个事件的类目，如解三角形、计算数列的和、求函数的极值等等。无论什么主题，图式中总是包含为那个类目中的所有客体或事件所共有的某些特征。因此，图式实质上是一种关于知识的认知模式。

就中学数学而言，图式不仅包含着数学知识本身，还包含着怎样利用这个图式的智力技能的程序性知识，以及对可能发生的情况进行预测和期望的信息。平面向量的知识已渗透到各个分支，特别是在几何中的作用更为突出，其次在复数、三角函数、物理中都有广泛的应用。随着教学的深入，它的优势会越来越明显，它运算简洁明快，化繁就简、有它的独到之处。扎实地学好、熟练地掌握这一章的内容，将会在今后的学习中受益匪浅。本章和“三角函数”、“三角变换”一起，构成了统一的教学模块，这也更好地体现向量在处理三角函数问题中的工具作用，也体现向量集形数于一身的特点。

高三学生有了一定的自学能力和概括比较能力，学生可以将知识加以梳理、沟通，使知识点之间发生联结，形成知识的网络系统，这样形成的认知图式便于学生理解、记忆和提取运用。首先根据学生的生活经验，创设丰富的情境，从大量的实际背景中抽象出向量的概念（数学模型），然后用数学的方法研究向量及其运算的性质，最后再运用数学模型去解决实际问题。简言之，现实世界中的问题→建立数学模型→对数学模型进行研究→利用数学模型解决问题。这样处理体现了数学知识产生和发展的过程，突出了数学的来龙去脉，有助于学生理解数学的本质，形成对数学完整的认识，达到培养学生的创新思维和理性思维的目的，同时也有助于数学应用意识的发展。

向量是数形结合的载体，向量的几何表示、向量加法的三角形运算法则等等都是从几何的角度对向量的研究，而向量的坐标表示、坐标运算就是用代数的方法来研究向量。在有关数量积的教学中更集中体现出数形结合的方法。

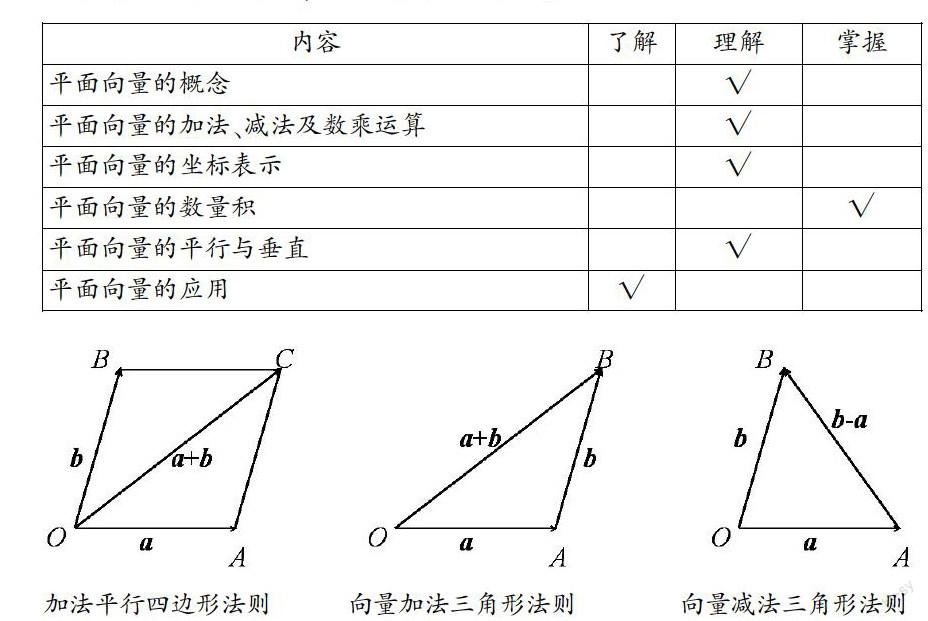
在学习向量后，有意识地将向量与三角恒等变形，与几何、代数之间的相应内容进行有机的联系，并通过比较，感受向量在处理三角、几何、代数等各不同数学分支问题中的独到之处和桥梁作用，认识数学的整体性。这样将有助于學生认识数学内容之间的内在联系，体验数学的发现与创造过程。如：讲授向量的加、减法时，根据加法的平行四边形法则（平移共起点，起点对角线）和三角形法则的特点，形象地将向量的加法总结为“首尾相连首尾连”或“平移首尾连，指向后终点”；将减法总结为“首同首连指向被减”或“平移共起点，指向前终点”。这样学生就能记得住、用得上、学得轻松。

4.结语

图式是人的头脑中关于外部世界知识组织形式，是人们赖以认识和理解周围事物的基础。经历用图式理论去学习平面向量，有助于学生更好地掌握向量，更有效地利用向量方法去解决某些几何问题、力学问题，更深刻地体会向量是一种数学工具，用向量运算的方法解决问题。

当然，图式理论在其他数学知识的学习中也有类似广泛的应用。实际生活中随处可见的速度、位移等，这些都是向量的实际背景，也可以用向量加以刻画和描述。

参考文献：

[1]Cook， G. Discourse[M]. Oxford： Oxford University Press， 1989， 1994.

[2]数学培训手册（苏教版），江苏教育出版社.

[3]吴庆麟等.认知教学心理学[M].上海科学技术出版社，2002.

[4]2012年江苏省高考说明（数学科）.