改进课堂教法优化课堂教学

翟严

为适应培养学生创新能力的教学目标，我们要有一套科学教法以适应新课程改革需要。本文就改进课堂教法，以优化课堂教学谈谈自己的一些看法。

1. 情景导入新课

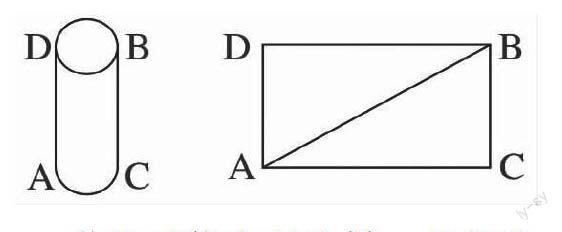
如在初三学习了圆柱有关知识而要学习勾股定理时，我课前提出一个问题：如下左图，有一只壁虎A晚上锻炼回来，又累又饿，突然发现离它不远处有一个圆柱形盒子上底边缘有一只蚊子B，为了尽快解决饥饿，它如何走路线才最短？

学生可能出现这样一些想法：沿着底部边缘爬到C处，再沿母线爬到B处；大部分同学认为由壁虎A位置沿侧面直接爬到蚊子B处；还有其它想法。究竟哪个正确，又如何说明它的正确性，我们教师必须找出一个让大家信服的理由。适当引导，尝试将圆柱展开（如上右图），寻求最短路线。而这恰好是圆柱展开图知识及勾股定理引入。这样既复习了圆柱展开图知识，又激起学生对勾股定理求知欲，问题才能迎刃而解，从而产生浓厚学习兴趣。

2. 教材联系生活实际

如现初一教材在幂的运算中有“读一读，估计100万粒大米质量”的例题。有位老师把其改成下面故事：古时候，有一个财主的一个佣人特别聪明，他为财主做了很多工作。有一次，财主高兴起来就表示满足佣人一个要求。佣人说：“就在收帐簿上放一些米吧，第1格放1粒米，第2格放2粒米，第3格放4粒米，然后依次放8、16、32……，一直放到第64格。”财主听后大笑，“你真是穷惯了，就要那么一点大米够你吃几天？”佣人说：“我怕你仓库没那么多大米，我只要第64格的大米。”同学们，你能帮这位财主算一算第64格大约有多少粒大米？有多重？这样的故事既激起学生学习兴趣，又使学生知道运用测量估计100万粒大米重量是解决问题的一个必然步骤。新教材及新教法趣味性强，又能引导用幂运算知识解决实际问题。这种教法既比单纯计算的旧教法有效，又能联系实际，用数学知识解决实际问题，达到学以致用目的。

3. 培养学生发散思维能力

如初一课本中有这么一道题：如图：

……，第n个图形需要多少条线段？

以往的教法是我们教师分析规律使学生明白即可；可这样学生思维得不到发散，从而没能创新求异。有位教师在教学时先和学生排摆魔方图，让学生先了解规律，然后让学生自己观察思考上面图形，就发现学生有如下几种方法：

因为第1个图形的三角形需要3条线段，以后每增加一个三角形就需要增加线段2条，即为：

三角形个数 线段条数

1 3

2 3+2

3 3+2+2

…… ……

所以第n个图形需要线段条数为3+2（n–1）。

也有同学作如下分析：

三角形个数 线段条数

1 1+2

2 1+2+2

3 1+2+2+2

…… ……

所以第n个图形需要线段条数为1+2n。

还有同学分析如下：因为每个三角形需3条线段，所以第n个图形原本应需要线段3n条，但从第二个图形起每两个三角形之间可以省一条线段，总共可省n–1条线段，因此第n个图形需线段条数为3n-（n-1）。

以上学生思维各异，但能从不同角度分析问题，找出解决方案。所以我们教学的着力点就是培养学生独立思考的习惯，培养发散思维，树立创新意识，形成创新能力。

4. 课堂考查

如我校一位教师引导学生探究出韦达定理后，给学生布置了这样一道题：

小华与小丽由于边说话边做同一道题目，小华看错了一元二次方程一次项系数，解得x1=2，x2=3；小丽看错了常数项，解得x1=6，x2=1；若方程二次项系数为1，你能否知道原方程正确答案？

这位老师以问题形式间接教育学生学习态度，还以问题形式激发学生探究运用韦达定理解决实际问题。这位老师把学生置于知识发现者、探究者位置上，引导学生主动独立地探究，这样就能培养学生逆向思维意识与解决问题能力。所以我们教师要对以往传授灌输式课堂教学方法进行改进，以优化课堂教学效果。

责任编辑潘孟良