加权核密度估计及其在沪深300股指收益率上的应用

宋文选

(浙江工商大学统计与数学学院，浙江杭州 310018)

加权核密度估计及其在沪深300股指收益率上的应用

宋文选

(浙江工商大学统计与数学学院，浙江杭州 310018)

由于金融数据的特殊性，对于其时变概率密度的估计和相应的累计分布函数的估计，可以通过非参数运用加权的核密度估计来捕捉每个时刻金融收益率的密度变化情况，这种方法中的重要参数，如带宽，可以通过最大似然函数和交叉检验进行估计.诊断检验可以通过向前一步预测的累计分布函数进行验证.对于这种追踪时变密度变化的方法，适用那些密度变化相对缓慢的数据上，并且该方法可以结合滤波进行递推估计.本文最后将此方法运用在沪深300股指.

加权核密度估计;时变累计分布;时变分位数

1 前言

金融收益率的研究主要着眼于传统的参数统计方法，这种方法大多数是将收益率数据放在正态分布的框架下进行研究的，但是不论从相关的理论研究还是实践的角度上看，金融数据收益率的分布并不服从正态分布的简单假设，更多的是存在明显的尖峰厚尾的现象［1］.像这种很难假定它服从某一固定分布的金融收益率，其更多的情况下分布是随时间变化的.对于这样时变的密度函数和分布函数我们可以运用非参数方法中的核密度估计.由于金融数据与时间有关，且传统的非参数是将每一个观测值等权重的看待，这样如果一味的照搬原来的理论方法将会使得非参数在刻画金融收益率的时变密度函数和时变累计分布函数时显的力不从心，也就是很难准确的追踪收益率的分布变化.因此借鉴于金融时间序列加权方法，结合核密度估计时变的分布的优势，本文试图运用加权的核密度估计来刻画金融收益率的变化情况.

2 加权核密度估计的理论

由核密度估计理可知，对于来自特定分布F(y)的样本量为T的观测值，其核密度估计在点y处的密度估计值为:

其中K(·)是核函数，h是带宽，通常核函数是关于原点对称且积分为1，主要的核函数有以下四种［2－3］:

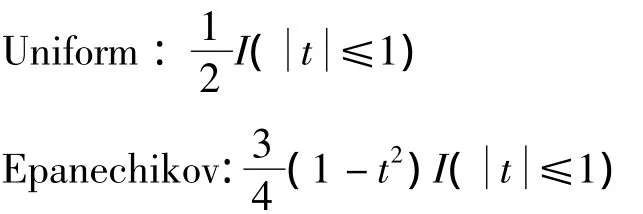
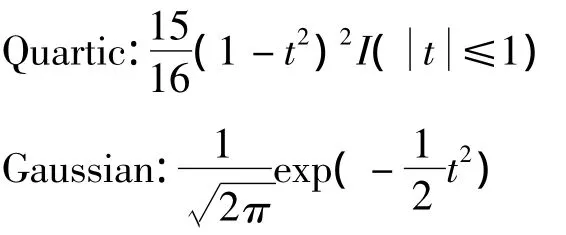
从定义上看核密度估计的优劣取决于核函数和带宽的选取上，事实上带宽的选取要远比核函数的选取重要.对于带宽的选取有很多种方法，如Silverman提出的拇指法则，Sheather和Jones提出的Plug－in方法，以及交叉核实(cross－validation)等.本文将采用最大释然估计的方法估计带宽.

在选定核函数后就可以敲定密度函数，竟而核密度估计下的累计分布函数也可以相应的确定下来，具体如下:

其中H(·)作为分布核可以通过对密度核函数积分获得.

为了更能准确的刻画每个时刻的密度函数，在传统核密度理论的基础上进行核密度加权，则(1)式变为:

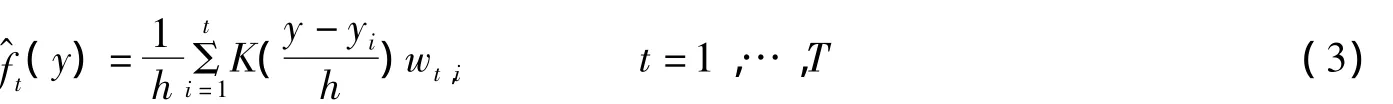
相应的累计分布函数为:

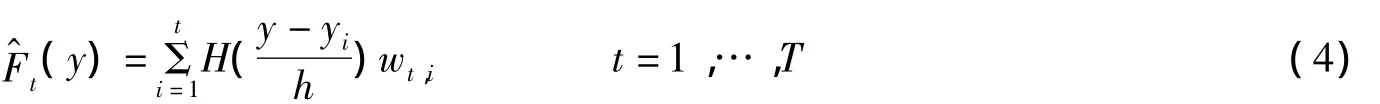
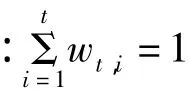
同样在平滑估计中时变密度函数的形式如下:

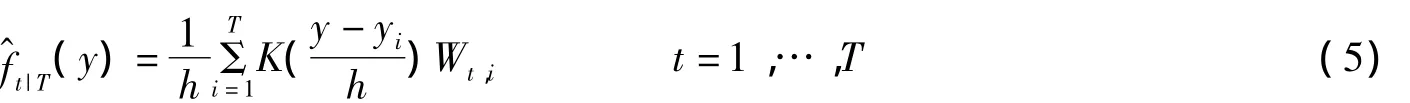
时变累计分布函数为:

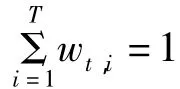
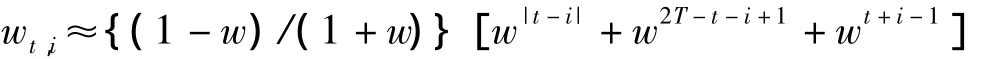
3 最优参数估计

对于模型中的两个重要参数带宽和平滑因子，我们将采用最大似然估计的方法使参数达到最优估计，滤波估计中参数的对数的似然函数为［5］:

其中wt，i(w)为公式(1)中的权重.变量m是估计前事先给定的值，该值主要依赖样本的大小，例如在估计时可以定义m为总样本的估计时平滑因子w必须定义在曲江(0，1］上，带宽h必须满足h＞0，由于对数中的数必须要等于零，所以当ft+1|t(·)需要选为非负的核密度函数，如高斯核，可以在理论上保证ft+1|t(yt+1)＞0，在估计时会遇到点y超出样本范围，这样会使得ft+1|t(yt+1)=0，在这种情况下，可以令ft+1|t(·)等于一个很小的正数值［6］.以确保对数下的密度值有意义.

对于平滑估计中的参数估计，需要最大化交叉核实准则即［7］:

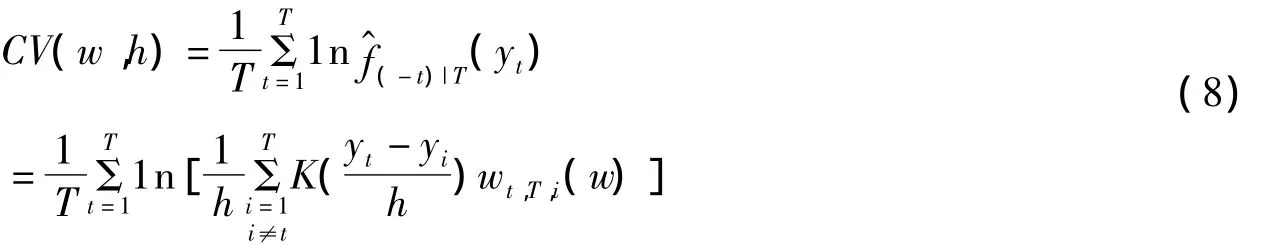
其中wt，T，i(w)与公式(3)中的权重相同.

4 时变分位数的估计方法

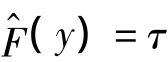
整个方法的估计过程是先通过最大似然估计或交叉核实准则求出最优参数:平滑因子w和窗宽h.然后在用公式(3)、(4)和(5)、(6)分别求出每个时刻下滤波和平滑的时变密度和时变累计分布函数.最后通过时变累计分布函数求出时变分位数.

5 实证分析

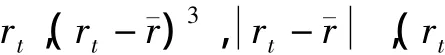
通过对收益率原始数据的进行最大似然估计，得到滤波的最优参数:w~=0.98823218，~h= 0.04406595，平滑估计下的最优参数:w^=0.97274846，~h=0.04405622.进行加权核密度估计时我们采用的是Epanechnikov核，图2显示了τ=0.05，0.25，0.50，0.75，0.95的沪深300股指收益率的时变分位数，从图像上可以看出加权后核密度估计能够很好的刻画分为数的变化，并且根据整个样本的信息来刻画分位数变化的平滑估计要比只是根据t时刻之前的信息进行的滤波估计好.

ARMA－GARCH残差

为了进行预处理我们选择学生t分布下的GARCH(1，1)的MA(1)模型.运用R软件对原始收益率进行GARCH估计，得到MA(1)参数，GARCH项参数，以及学生t分布的自由度的分别为Coefficient(s):

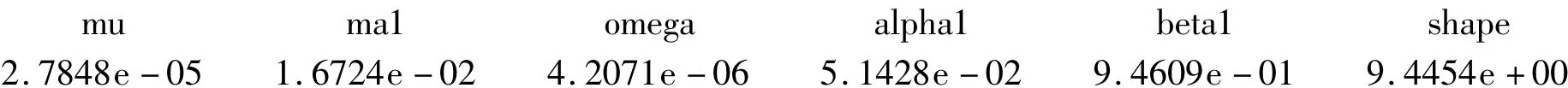
图1

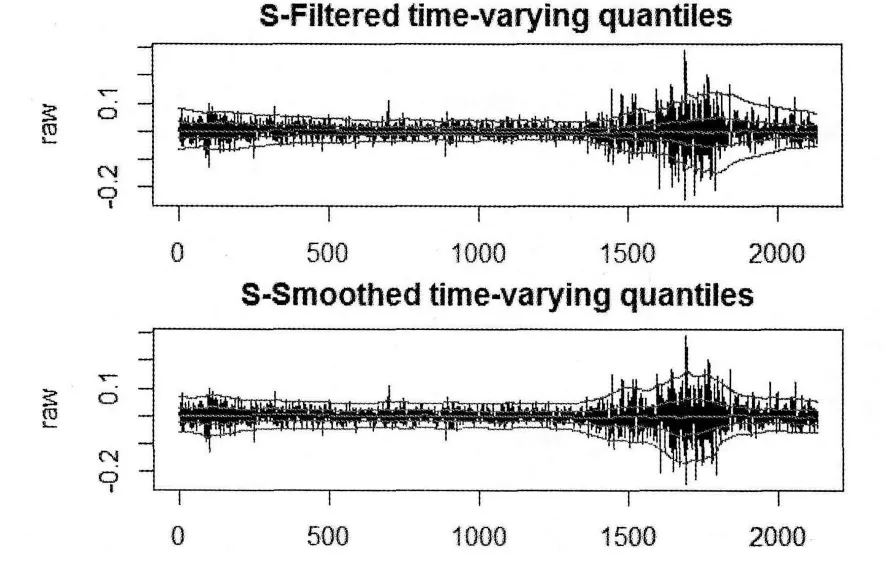
图2

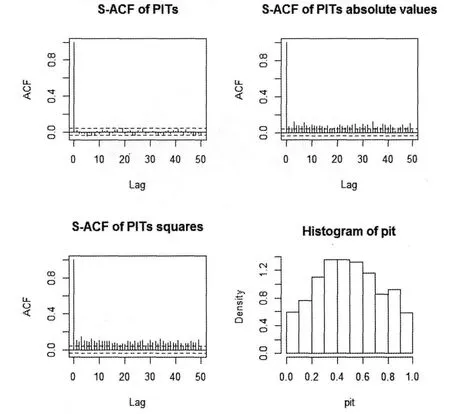
图3

同样收益率经过GARCH模型转化后，对GARCH标准残差进行最大似然估计，得到滤波的最优参数=0.99863512，~=0.04182415，平滑估计下的最优参数=0.99251618=0.04003711.

图4描述了GARCH标准残差的τ=0.01，0.05，0.25，0.50，0.75，0.95，0.99的时变分位数，正如预期所料，基本上每一个时刻分位数保持不变，也就是说残差基本上来自于一个固定的分布函数.

经过预处理后，从图5中可以看出，残差的PIT在绝对值和平方都不在具有较强的相关性，并且与图3中的PIT直方图相比，残差PIT的直方图表现出了均匀的形态，不在是以往的凸峰形态，也进一步说明了残差PIT满足均匀分布.

最后我们通过离差(dispersion)和偏度(skewness)［9］两个指标来观察每个时刻的离差(dispersion)和偏度(skewness)的变化近而刻画每个时刻的分布变化情况.

Dispersion指标定义如下:

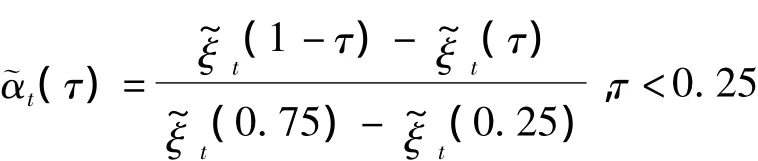
图4

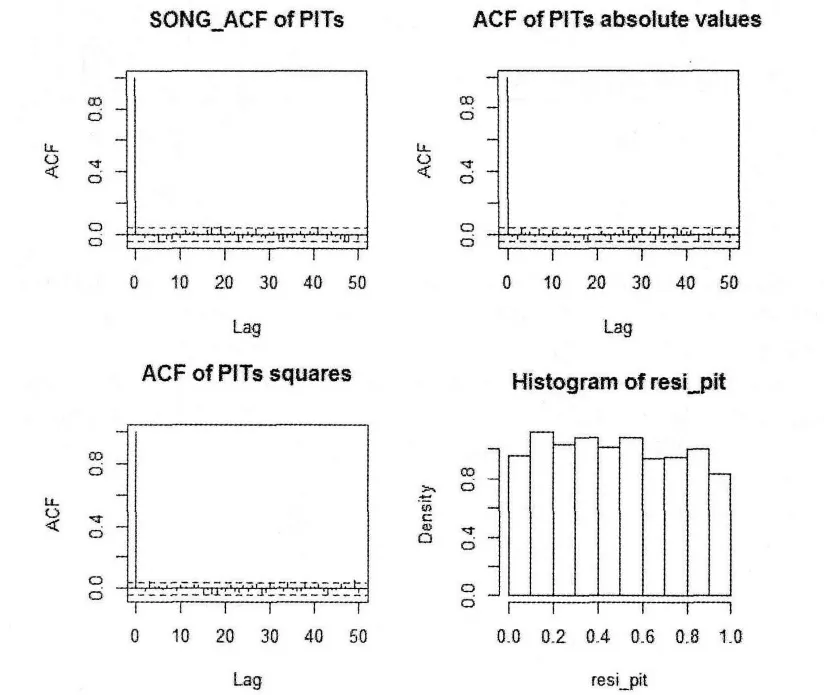
图5

偏度(Skewness)指标定义如下:

如图6τ=0.01时离差(dispersion)指标基本上为4.0.τ=0.05时离差(dispersion)指标基本上为2.6，注意标准正态分布的这两个值分别为3.45和2.66，所以可认为GARCH标准残差基本上接近标准正态分布.偏度(Skewness)指标最大值是1，此时分布函数右偏，最小值为－1，密度函数左偏.当该值等于零时，分布函数是对称的，从偏度(skewness)图上可以看出，GARCH标准残差的分布基本上是对称的.

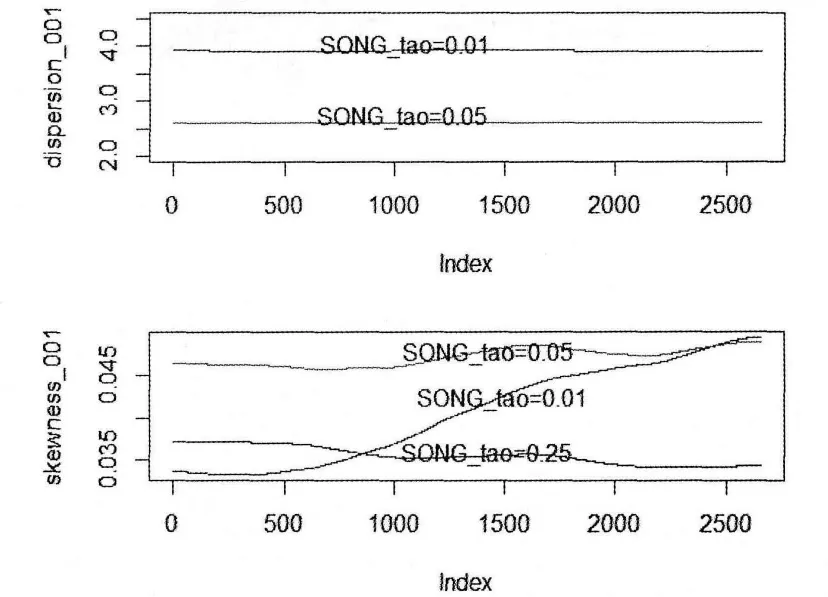
图6

该种方法估计的时变分位数也可以应用在Copulas的有关理论中，比如我们要计算出两个不同金融市场的同时出现在某一分位数一下的概率，便可以采用加权核密度的方法估计出如图7，蓝色圈标记的表示分位数低于0.05分位数的状态，当然这只是针对单一金融市场标出的记号，对于多个金融市场可以同样类似的进行.

6 结论

本文将核密度估计与时间序列的特性有效的结合在一起，构造了加权核密度估计的方法，并将其应用在沪深300股指收益率上.从以上的研究结果可以看出该种方法很好的捕捉了密度函数的变化.同时对于时变分为数的估计也提出了很好的方法，相比由进行排序计算分位数的方法而言，该种分位数的计算不会产生交叉，并且能够较好的包络金融收益率的变化.当然这种方法的不足之处就是，它只能描述那些密度函数变化缓慢的金融序列.对于有些金融数据波动性的突然增加，我们需要通过GARCH模型对收益率进行调整，才能更好的应用此种方法.加权核密度估计在收益率的应用或许能够为证券期货市场的研究和投资提供很好的借鉴意义.

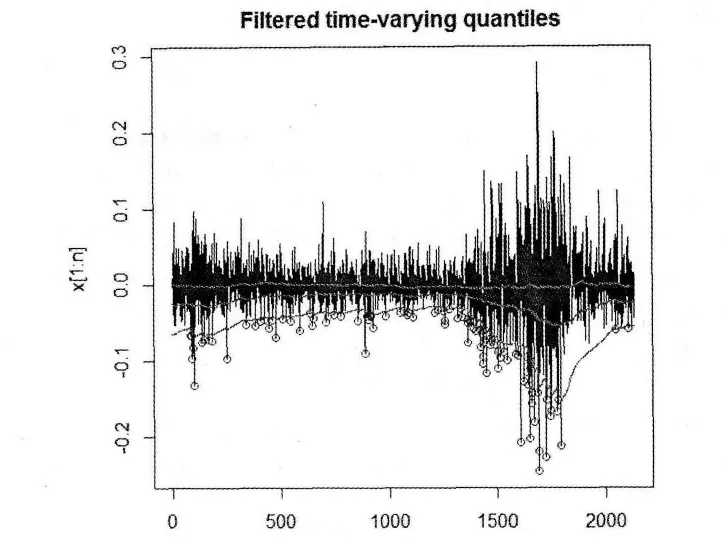
图7

［1］镇志勇，李军.非参数核密度估计在恒生指数收益率分布的应用［J］.统计与决策，2011(9):22－24.

［2］陈希孺，柴根象.非参数统计教程(第一版)［M］.上海:华东师范大学出版社，1993.

［3］叶阿忠.非参数计量经济学(第一版)［M］.天津:南开大学出版社，2003.

［4］朱红伟.加权核密度估计及对我国消费支出的分析［J］.山西财经大学学报，2006，28(2):40－41.

［5］E.J.Wegman.Nonparametric Probability Density Estimation［J］.Technometrics，1972(14):533－546.

［6］区诗德，等.股票收益率密度的非参数估计及投资策略［J］.统计与决策，2006(3):4－6.

［7］Azzalini A.A note on the estimation of a distribution function and quantilesby a kernelmethod［J］.Biometrika，1981，68(1):326－328.

［8］Berkowitz J.Testing density forecasts，with applications to risk management［J］.Journal of Business and Economic Statistics，2001，19 (4):465－474.

［9］Sheather S.J.，Marron J.s.Kernel quantile estimators［J］.Journal of the American Statistical Association，1990，85(410):410－416.

Weighted Kernel Density Estimation and Its Application in Hu Shen 300 Index Futures

SONGWen－xuan
(School of Statistics and Mathematics，Zhejiang Gong Shang University，Hangzhou，310018，China)

Due to the particularity of financial time series，a time－varying probability density function and the corresponding cumulative distribution function can be estimated by using a kernel and the weighted time series data.There are two important parameters，including the bandwidth and smoothing factor，which can be estimated respectively bymaximum likelihood and Cross validation.Diagnostic checks can be conducted by predictive cumulative distribution function.If the density of time series changed quickly，thismethod will fail to capture the characteristics of the series.Without doubt，this technique can be combined with a filter for scale.Finally，this paper applied thismethod to data on the index futures of Hu Shen 300.

weighted kernel density estimation;time－varying cumulative distribution;time－varying quantiles

F224;F832

A

1672－2590(2015)03－0057－08

2015－03－23

宋文选(1988－)，男，河南信阳人，浙江工商大学统计与数学学院硕士研究生.