滚子凸度偏移对圆锥滚子轴承接触应力的影响
夏新涛,董淑静,孙立明
(1.河南科技大学,河南 洛阳 471003;2.洛阳轴研科技股份有限公司,河南 洛阳 471039;3.河南省高性能轴承技术重点实验室,河南 洛阳 471039;4.滚动轴承产业技术创新战略联盟,河南 洛阳 471039)
圆锥滚子轴承具有可同时承受轴向和径向载荷、承载能力大、滚动摩擦小、刚性好、安装简单等优点,在汽车、铁路、机床、矿山、冶金等大型机械设备中被广泛应用[1-3]。对数凸度滚子加工时的凸度偏移误差和装配中的滚子偏移误差对其使用性能和寿命有重要影响,因此需确定合理的误差范围[4-8]。
凸度偏移量的确定对圆锥滚子轴承的设计应用有指导意义。文献[9]用有限元方法分析了圆柱滚子轴承在一定载荷条件下的应力分布情况,通过分析滚子偏移情况给出了对数曲线滚子修形时应控制的凸度偏移量。文献[10]分析了适用于不同修形滚子的寿命计算公式,表明对数曲线修型对于提高轴承寿命有一定的意义。下文以双列圆锥滚子轴承353112为例进行有限元分析,研究其凸度偏移量的合理范围及对接触应力分布的影响。
1 圆锥滚子轴承有限元模型
1.1 滚子凸度偏移
圆锥滚子的设计与加工主要考虑对其工作表面特性的要求,即滚子的凸度和球基面。对于对数曲线的凸度滚子,可以采取以滚子有效长度中心为坐标原点,向滚子大端方向略微移动的方法,实现滚子两端不同的凸度量。对数曲线滚子凸度偏移简图如图1所示,圆锥滚子的凸度偏移误差是指修形后对数曲线滚子上的对称点与坐标原点O产生的偏移量s。

图1 对数曲线滚子凸度偏移
1.2 建模
卡车轮毂用双列圆锥滚子轴承353112的结构简图如图2所示,主要结构参数见表1。
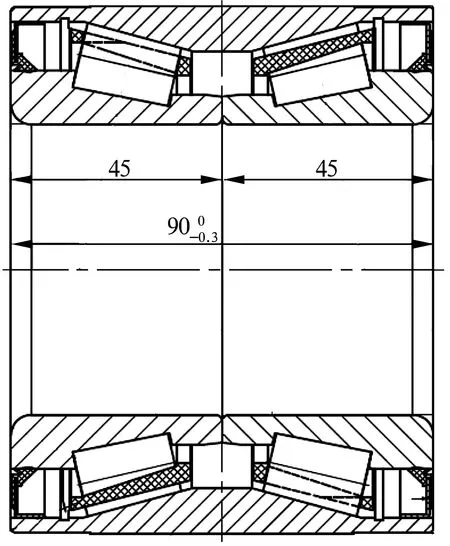
图2 圆锥滚子轴承结构示意图
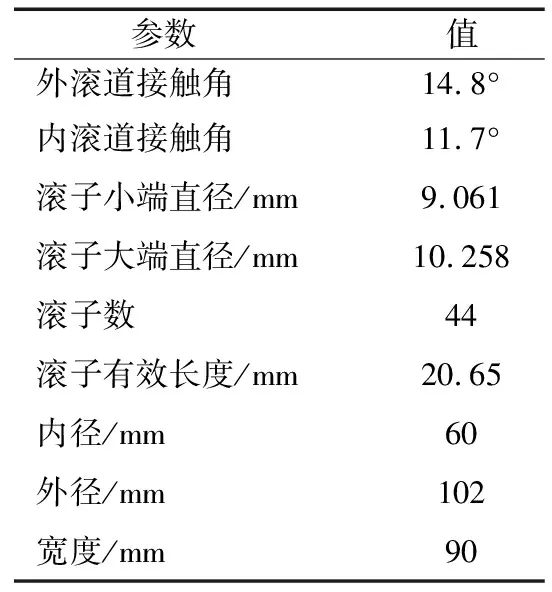
表1 轴承主要结构参数
轴承材料均为GCr15,滚子与内外滚道表面接触摩擦因数为0.1,材料弹性模量为206 GPa,泊松比为0.3。滚子受的最大法向载荷为7 000 N。因其结构对称,故仅需建立1/2有限元模型。
用有限元软件建立模型时,忽略对轴承应力影响不大的倒角和边棱,也不考虑轴向游隙、径向游隙及润滑油膜对接触应力的影响。单元类型采用8节点的solid185单元,每个节点有3个自由度,其可用来模拟均质结构固体。对内外圈滚道与滚子接触位置切分之后,设置整体单元尺寸进行映射网格划分,其他部位采用扫略网格划分法,加密处的最小网格单元小于接触半宽长度,如图3所示。
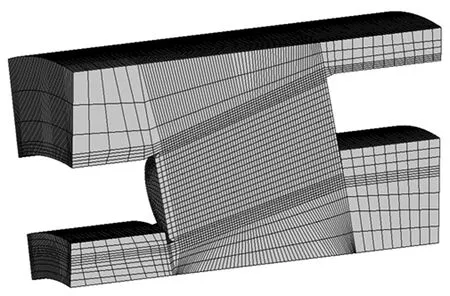
图3 有限元模型
以轴承内外圈为目标面创建接触对,滚子表面为接触面,接触摩擦因数为0.1。边界条件设置:对轴承各截面进行对称约束,外圈与轴承座为过盈配合,故外圈外表面全部约束,内圈约束轴向自由度。加载时取内圈对称中心的结点做为主节点,选择相邻节点为从节点,之后选取内圈内表面所有节点耦合y向(径向)自由度,在主节点上施加载荷即可。
2 结果及分析
无凸度偏移时,滚子与内外圈滚道在沿滚子素线方向的应力分布如图4所示。由图可知,滚子与内圈的最大应力值在滚子中心偏左的位置。但圆锥滚子与外圈接触的最大应力值靠近滚子中心位置,且应力分布对称均匀。
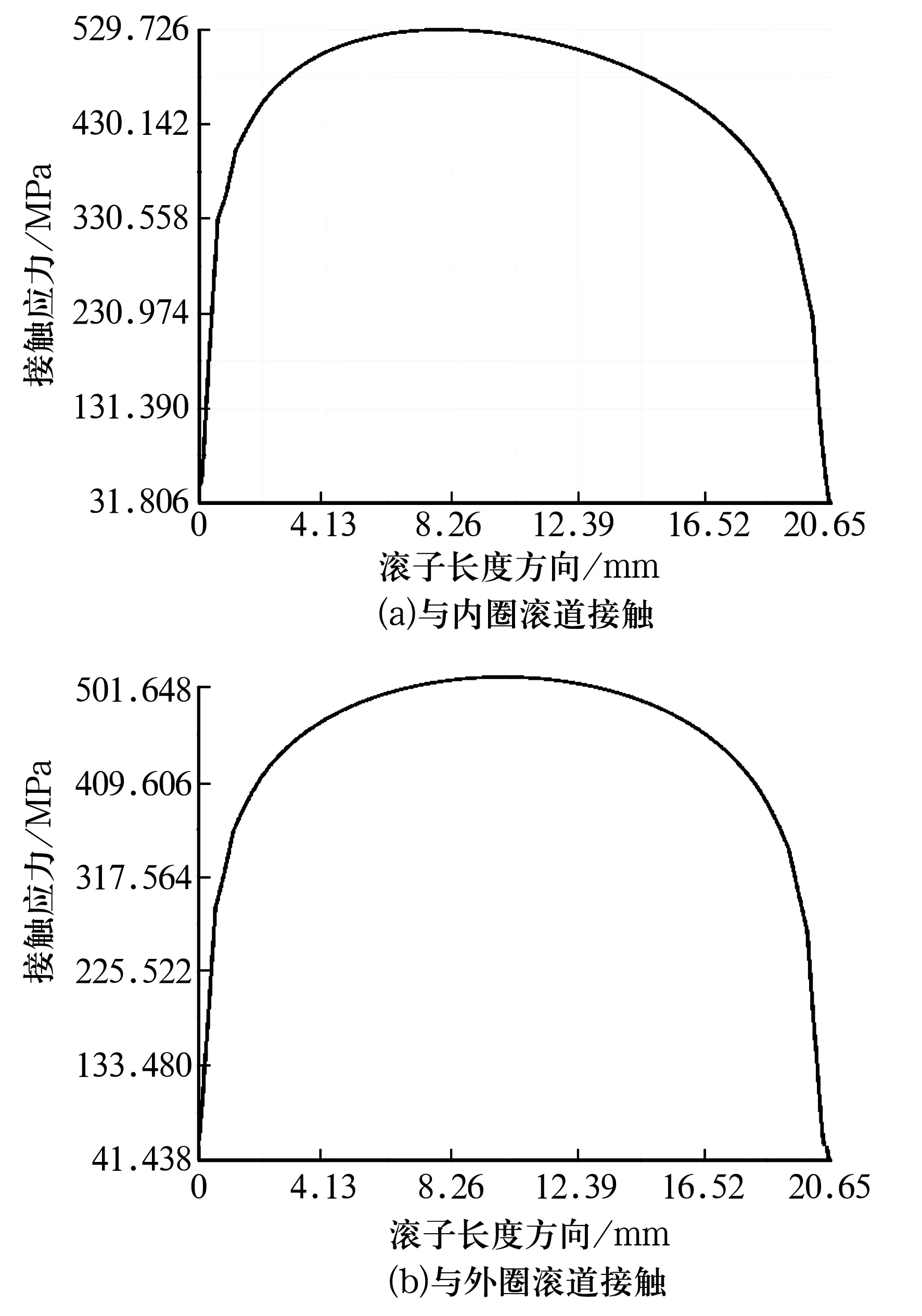
图4 无凸度偏移滚子与内、外圈接触的接触应力
滚子凸度中心向滚子大端偏移0.4 mm与向滚子小端偏移0.2 mm时,滚子与内圈滚道的接触应力沿滚子素线的分布如图5所示,接触应力并没有对称均匀分布。
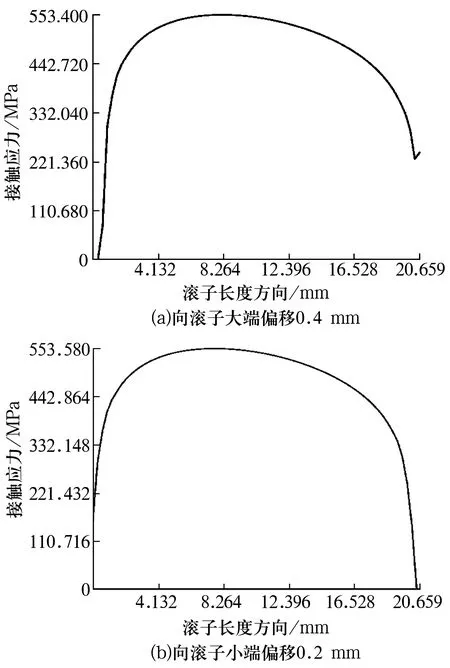
图5 滚子凸度中心偏移时与内滚道的接触应力
滚子凸度中心向两端偏移时,滚子两端与内圈滚道之间接触应力的变化如图6所示。由图6a可知,在相同条件下,随着凸度偏移量的增大,滚子小端的接触应力逐渐减小,而滚子大端的接触应力迅速增大,在偏移量增大至0.2 mm以后,滚子两端的接触应力差值迅速增大。凸度中心向滚子小端偏移的情况如图6b所示,随着偏移量的增大,滚子两端的接触应力差值开始明显增大。由此可知,滚子素线的凸度偏移会导致滚子两端与滚道的接触应力出现不对称性和非均匀性。
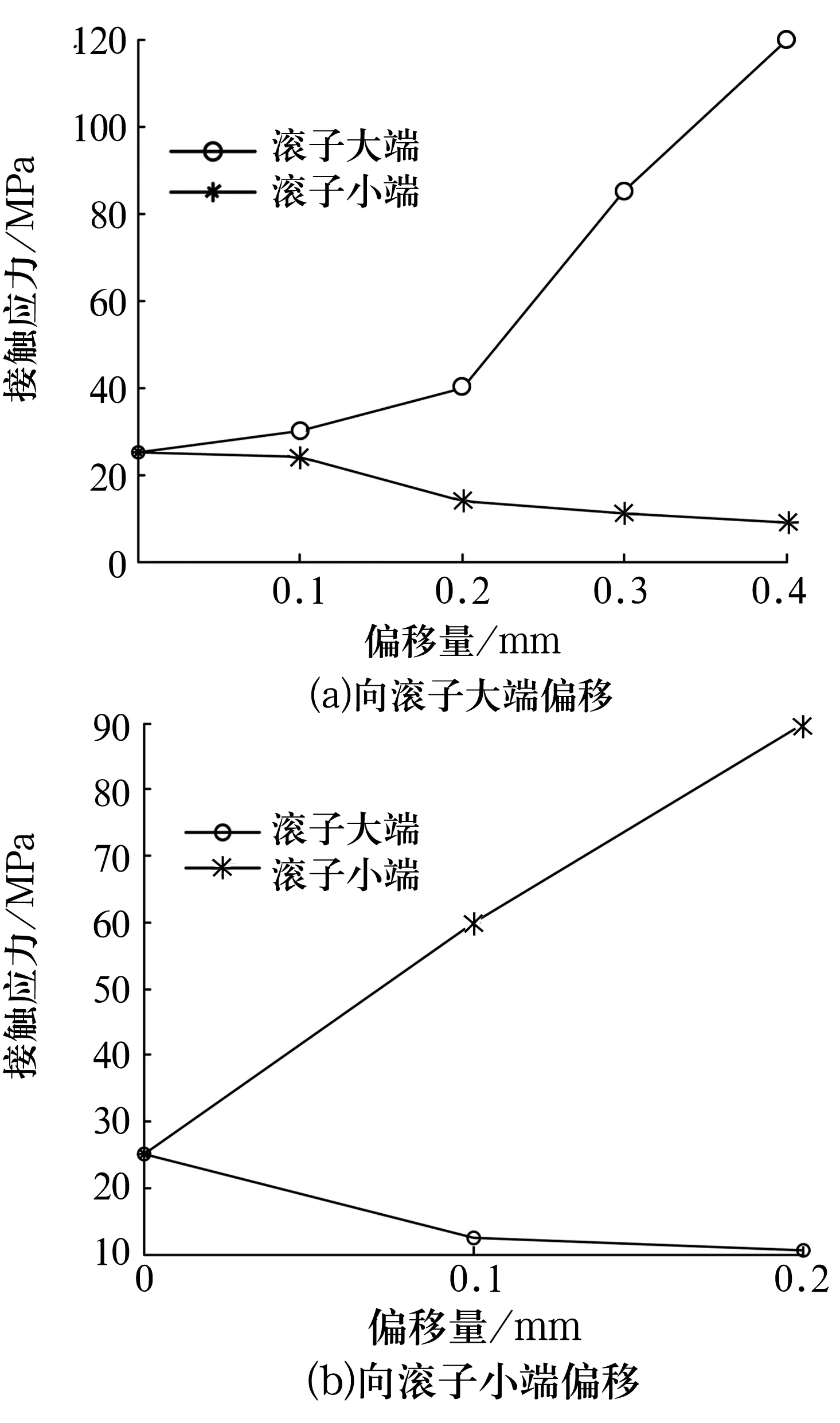
图6 凸度偏移量对滚子两端与内滚道接触应力的影响
图7为定量评估凸度偏移对滚子两端接触应力的影响。随着凸度偏移量的增加,滚子两端接触应力的相对差值呈非线性增加,在向大端的凸度偏移量大于0.1 mm后,滚子两端接触应力的相对差值迅速增大,表明向大端偏移0.1 mm是一个转折点,此时,滚子两端的相对差值约为20%,满足工程上所允许的最大相对误差25%。而凸度中心向小端偏移时,滚子两端接触应力的相对差值较大,不能满足工程条件。因此,为满足353112圆锥滚子轴承应力分布的均匀性与对称性,对数曲线滚子的凸度中心应控制在向大端偏移0.1 mm以内,且不宜向小端偏移。

图7 凸度中心偏移量与滚子两端应力相对差值的关系
3 结束语
对数曲线滚子修形时,应严格控制滚子凸度中心偏移量,否则接触应力会呈现出复杂的非对称性,凸度中心可向大端适量偏移。对353112轴承,滚子凸度中心应控制在向大端偏移0.1 mm以内,且凸度中心不宜向滚子小端偏移。

