双树复小波和中值滤波在机械故障监测中的应用

邱爱中,崔晓,张海泉,邱大为

(1.郑州师范学院,郑州 450044；2.中国科学技术大学,合肥 230000)

机械故障诊断中的传感器往往处于恶劣的环境中，直接获取的原始信号必然含有大量噪声，必须通过降噪才能获取有用的信号信息特征。弱故障信号的提取和恢复一直是机械故障诊断的难点和要点，例如，动力装备的转子、齿轮、轴承等部件在故障初期，不明显的故障信号往往比较微弱，有时完全淹没在强噪声中，而且信号中往往同时混杂了白噪声和脉冲噪声。

为提高降噪效果，文献[1-2]指出常规的离散小波变换会产生伪Gibbs效应，改进措施是采用atrous算法进行非降采样的小波变换(Undecimated Discrete Wavelet Transform，UDWT)。然而该变换会使计算量猛增，且冗余信息不易消除，增加后续数据处理的难度。文献[3-5]指出复数小波在数据处理上相对冗余且计算量较少，不足之处是要构造完全重构的逆滤波器在实践中非常困难。而双树复小波变换(Dual-Tree Complex Wavelet Transform，DT-CWT)[6-7]完全重构的滤波器较易实现，且具有近似平移不变性、能完全重构、相对较小的计算量等优点。文献[8-9]认为中值滤波能较好抑制脉冲噪声，且具有良好的边缘保持特性，可作为非线性滤波的典型代表。

因此，研究了复数小波的构造，简化了滤波器的设计，在此基础上提出一种基于双树复小波和中值滤波相结合的消噪方法。

1 基于DT-CWT和中值滤波的降噪法

1.1 双树复小波构造的数学模型

双树复小波的实现是通过一对滤波器组同时处理输入数据[4-6]，其包含2个平行的小波分支(小波树)，2棵树中的实数滤波器h0(n)和h1(n)，g0(n)和g1(n)分别表示1个共轭正交滤波器对。

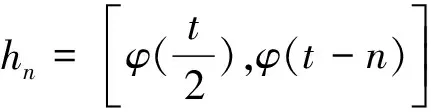
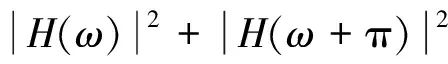
H(0)=1。

(1)

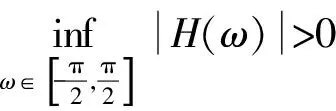
(3)

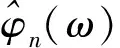
设φ为正交尺度函数，h={h0,h1,…,hN}是对应的双尺度方程滤波器，则构造这样的正交小波时滤波器应满足

(4)

(5)

其中，当n=0时，δ=1；n≠0时，δ=0。

1)小波函数ψ(x)需具有m阶消失矩特性。

2)低通滤波器函数系数要满足

(6)

3)H(ω)在ω=π处存在m重零点。

满足以上条件可得

(7)

得到滤波器后，令

(8)

在0～2π范围内求出|H0(ω)|的上界值，如果其不大于2m-1，则H就为所求滤波器函数。联立(4)～(8)式就可以构造符合要求的各种互为Hilbert变换的正交小波。

1.2 中值滤波

中值滤波的原理是设计一种滑动窗口处理抽样数据，用滑动窗口中心位置的信号抽样值取代当前窗口内所有抽样的对应中位值。例如，假设数据处理的窗口抽样长度n=2k+1(k为正整数)，那么第i时刻输入信号序列在窗口内的抽样样本就为(xi-k，xi-k+1，…，xi，…，xi+k-1，xi + k)，则此时中值滤波器的输出为

yi=med(xi-k，xi-k+1，…，xi，…，xi+k-1，xi + k)，

(9)

式中：med()表示取此时处理数据窗口内所有抽样数的中位数。由此可知，窗口宽度若取为n=2k+1，如果信号中混杂有脉冲信号噪声，信号抽样序列中脉冲宽度小于或等于k的脉冲噪声将被去除；而当脉冲噪声宽度大于或等于k+1抽样间隔时，脉冲噪声未得到抑制，仍被保留。所以中值滤波对脉冲信号宽度满足上述条件的脉冲噪声有较好的去除抑制作用，但对随机白噪声的抑制能力却微乎其微[7]。

1.3 基于DT-CWT和中值滤波的降噪方法

在离散正交复小波变换构造的基础上，与中值滤波数据处理原理有机结合，提出了该降噪思想，充分考虑了DT-CWT的完全重构降噪特性，并可同时抑制白噪声和脉冲噪声，其具体步骤为：

1)将被检测信号用DT-CWT进行变换，得到2棵树的正交离散复小波每层的小波系数。

2)由于噪声主要集中在小波分解细节系数中，故需对每层的细节系数首先进行中值滤波处理，再实施噪声估计和阈值选择，进行阈值降噪滤波，而让尺度系数保持不变。

3)利用小波变换软阈值估计方法，获取降噪阈值，对细节系数实施软阈值降噪处理。

4)将2棵树的系数按照上述方法进行阈值修改后，对系数再进行逆DT-CWT，重构得到降噪后的被分析信号。

2 仿真分析

2.1 非平稳、非线性信号

为了验证降噪效果，进行MATLAB仿真检验，利用该软件产生具有代表性的3种非平稳信号Heavysine，Bloeks，Bumps，并在其中加入白噪声和有色噪声，然后用上述算法及一些常规方法对染噪信号进行降噪处理，并对比降噪效果。

利用降噪处理后重构信号的信噪比Rsn和均方差误差Rmse对这些降噪算法进行对比评判。评判的标准是降噪后信号的信噪比越高，均方差越小，则降噪效果越好；反之，说明降噪效果相对较差。评判的公式为

(10)

(11)

不同方法对应的信噪比和均方差见表1。由表可知：基于DT-CWT和中值滤波的降噪方法能够获得比其他降噪法更高的信噪比，显示出较好的对白噪声降噪效果。

表1 不同方法消噪处理后的结果

某非平稳、非线性染噪信号及不同降噪方法处理后的结果如图1所示。从图中可以看出：基于DT-CWT和中值滤波的降噪方法降噪效果相对较好，可以更好地保留强高斯白噪声背景下的信号特征的细节信息，更好地再现原始无噪信号，其他方法降噪后仍含有较大噪声，原始信号细节信息有所丢失。

图1 不同方法对染噪信号的降噪结果

2.2 冲击信号

混杂白噪声和脉冲噪声的染噪信号及不同方法对应的降噪结果如图2所示。从图中可以看出：其他方法只能抑制白噪声，对去除脉冲噪声无能为力；而基于DT-CWT和中值滤波的降噪方法可以更好地去除强噪声，还原原始的无噪信号，保留强脉冲噪声背景下的弱信号特征信息，实现更好的降噪效果。

图2 不同方法去除脉冲噪声的效果比较

3 水轮机轴承故障监测的试验实例

以某水电站水轮发电机轴承为试验对象，长期不间断监测其工作情况。水轮机型号为HL220-LJ250，采用29492型推力调心滚子轴承,内径460 mm，外径800 mm。在水导轴承附近加装涡流传感器测量轴承振动信号，采样频率为512 Hz，采样长度为1 024。不断记录得到一列信号数据，发现一水轮机轴承的振动峰值及均方根值等观察监测指标从2014年6月5日后逐渐增大，测得故障振动信号如图3a所示，由于测量环境恶劣，测量受强烈水流冲击的影响，故障信息基本无法识别。

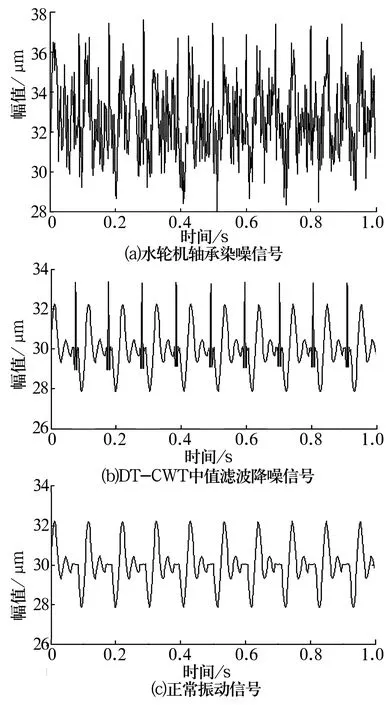
图3 水轮机轴承冲击故障信号的提取

为了确定故障源并验证本研究效果，采用基于DT-CWT和中值滤波的降噪方法对此振动信号进行降噪处理，结果如图3b所示，原始振动信号中掺杂的由水流冲击产生的强噪声被有效地剔除。与该轴承正常振动信号(图3c)对比可以看出，该水轮机出现了周期性的振动冲击。

将轴承取出并拆套，发现其内圈产生了局部损伤，叶轮转动时滚动体转动到损伤部位时产生明显的冲击力，导致该机械故障信号的产生。故障信号的冲击频率为9.51 Hz，与图中监测的频率正好吻合。更换轴承后重新安装，发电机恢复正常运转，信号恢复正常。

4 结束语

仿真试验和应用实例分析表明，基于DT-CWT和中值滤波的降噪方法可获得比常规小波降噪以及CWT降噪更高的信噪比，不仅能抑制高斯白噪声，去除偶然的短暂脉冲噪声，还能有效地提取有用的周期性冲击信号，但对单个偶然短暂的有用脉冲信号的提取却无能为力。

机械故障通常表现为周期性的冲击特征，基于DT-CWT和中值滤波的降噪方法可以消噪后保留和提取轴承、齿轮等故障的周期性冲击信号特征信息，根据其周期性冲击所对应的特征频率和信息对其进行简便故障识别，比常用的频谱分析方法更为简便，为进一步的频谱分析提供基础。