水利工程坐标系建立方法探讨

崔建明

（山西省水利水电勘测设计研究院 山西太原 030024）

在水利工程建设中，国家统一坐标系统往往不能满足工程建设的需要，所以必须针对不同的工程建立相应的工程坐标系统。工程坐标系统的建立首先是投影变形及变形改正问题；其次，才是工程坐标系统的建立。

1 高斯投影变形和变形值大小的影响

1.1 投影变形分析及变形值改化的探讨

1.1.1 高斯投影变形分析

通过高斯投影的理论研究，我们知道当经度L等于常数时，随着纬度B的增加，高斯坐标的x值增大，而y值减小；又因cos（-B）=cos（B），所以无论B值为正或为负，y值不变。这就是说，除中央子午线投影外，其他子午线投影后，均向两极收敛，并对称于中央子午线和赤道。

当纬度一定时，随着经度的增加，x值和y值都增大。所以在椭球面上投影后仍成为对称的曲线，且对称于赤道线圈。

1.1.2 投影变形值探讨

1投影变形值

由高斯投影分析可知：距离中央子午线愈远的子午线，投影后弯曲愈厉害，长度变形也愈大。

1）地面水平距离换算至椭球面上的变形分析

假设地面水平距离归算到参考椭球体面上的长度变形设为Δs1，则：

式中：Hm——归算边高出参考椭球面的平均高程；

s——观测边长；

RA——归算边方向参考椭球法截弧曲率半径。

2）再将椭球面上的距离换算至投影面的变形分析

设椭球面上大地线长度S投影在高斯平面上，其变形值为Δs，则：除中央子午线外，其余都变形，且均变长，具体变形量的计算，见公式（2）。

式中：Δs——参考椭球面上大地线长度S投影到高斯平面距离的变形值；

S——椭球面上两点大地线长度；

ym——大地线投影后始末两点横坐标绝对值的平均值（此横坐标应去掉500 km的常数和投影带号）；

Rm——参考椭球的曲率半径。

2投影变形值改化

归算边长的相对变形的近似关系式为；

即Δs1/s与归化高程成正比。设RA=6 371 km，Hm为100～2 000 m时，依式（2）和式（3）计算每公里长度投影变形值及不同高程面上的相对变形，见表1：

表1 Δs1、Δs1/s0与Hm的关系

将参考椭球体面上的边长s0归算到高斯投影面上时，其长度将会增大Δs2，

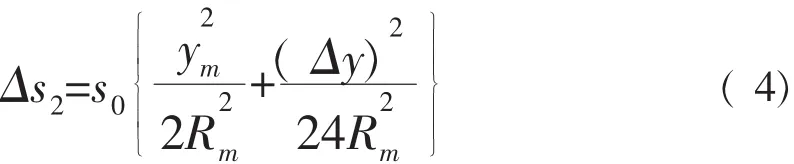
投影边长的相对投影变形的近似关系式为：

式中s0=s+Δs1，即s0为观测边长s归算到参考椭球面上的边长，ym为观测边两端点横坐标平均值，其差数为Δy，Rm为参考椭球面在测距边中点的平均曲率半径。设测区平均纬度B=36°，Rm=6 371.6 km，Δy取最大值1 km，依公式（4）和公式（5）计算每公里长度投影变形值及相对投影变形值见表2。

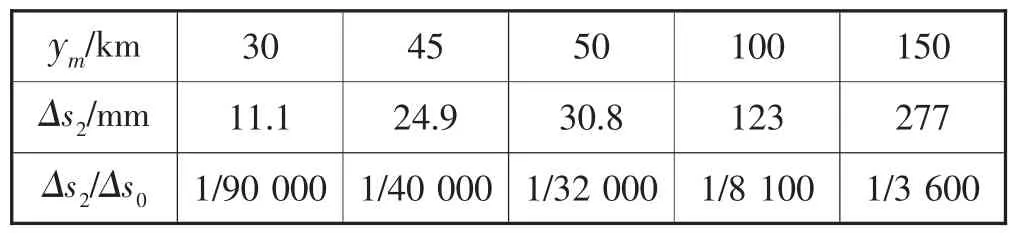
表2 Δs2、Δs2/s0与ym的关系

1.2 高斯投影后长度变形值的允许值

我国《城市测量规范》和《工程测量规范》对控制网的长度综合变形值的允许值做出了明确规定，即综合变形值应小于2.5 cm/km，其相对变形值不超过1/40 000。

2 工程坐标系的建立

2.1 国家统一3°带平面直角坐标系统的建立

1）国家统一3°带平面直角坐标系统建立的前提

由表1、表2可见，当测区平均高程在160 m以下，ym绝对值不大于45 km时，其观测边长投影变形值 Δs1、Δs2均小于2.5 cm， 或 Δs1+Δs2＜2.5 cm时，其长度变形不会小于1/40 000。在这样的前提下，可直接采用国家统一3°带高斯平面直角坐标系统。

2）国家统一3°带高斯平面直角坐标系统的建立

国家统一3°带高斯平面直角坐标系统在我国已经建立完毕，这里不再谈论。

2.2 “抵偿”坐标系统的建立

2.2.1 抵偿高程值的选取

例如某测区海拔Hm=1 002 m，最边缘距中央子午y0=35 km，当s=1 000 m时，则其变形值为：

而 Δs1+Δs2=-0.142 m

显然，其变形值超过了2.5 cm/km。为使变形值小于2.5 cm/km，就必须建立高斯正形投影3°带高程抵偿平面直角坐标系统。

设测区的平均高程为Hm（大地高），某水利工程中心附近某点的3°带坐标系中的横坐标为y0，为使测区中心处的长度变形完全被抵偿，须使高程归化面低于测区平均高程面，依据下式：

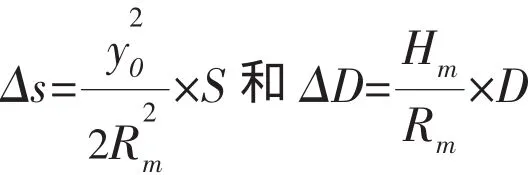
式中： ΔD为地面距离投影至参考椭球面长度的缩短值；Hm为测区平均高程；D为地面两点间的距离；Rm为参考椭球的曲率半径，通常取值为6 371 km。

可推出公式（6）

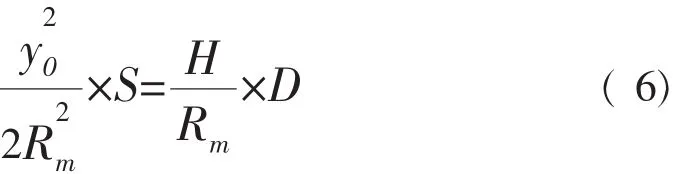
设抵偿高程归化至大地高为，则：

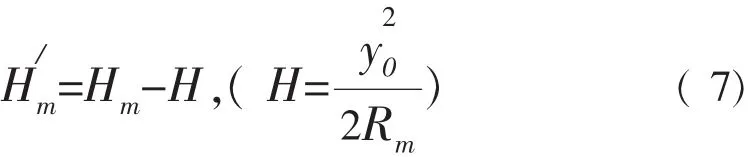
例如：某测区平均大地高为1 002 m，对于y0为35 km，则H=96.14 m，依据公式（7），则抵偿高程归化面大地高=905.86 m。

投影变形值为：

由此可见，通过抵偿高程归化，则投影变形值完全抵消。

2.2.2 抵偿坐标系建立方法

1）国家统一高斯平面直角坐标系根据高斯反算公式换算成大地坐标；

2）把大地坐标换算成同一基准面下的空间直角坐标；

3）空间直角坐标根据新的椭球参数（将原椭球长半轴加上得到新的长半轴，扁率不变）换算成大地坐标；

4）大地坐标进行高斯投影换算成平面直角坐标，此坐标系即为工程坐标系。

2.2.3 高斯正形投影任意带平面直角坐标系的建立

1）任意带中央子午线经度的求取

设某大型水利工程相对参考椭球面的大地高为Hm，为使工程中心边长综合变形为零，设抵偿中央子午线距离测区中心的距离为ym，则有：

则

任意投影带的中央子午线经度L0可按下面两式计算：

式中：B、L——测区中心位置的经度和纬度；

Rm——参考椭球曲率半径；

L1——测区中心经度L与任意投影带的中央子午线经度L0的差值。

2）任意带平面直角坐标系建立方法

方法是：把地面观测结果归算到参考椭球面上，但投影带的中央子午线不按国家3°带的划分方法，而是依据抵偿高程面归化长度变形而选择的某一条子午线作为中央子午线，从而建立其坐标系统。

2.2.4 假定平面直角坐标系的建立

1）该坐标系的适用条件

假定平面坐标系（包括建筑坐标系），是在测区附近没有可资利用的控制点，或暂无联测条件，或为某种工程建筑施工之用而建立的一种坐标系统。这种坐标系的建立应满足以水平面直接代替水准面的条件，即测区面积应小于100 km2。

2）建立方法

假定平面直角坐标系是以独立测区内平均水准面的切平面作为坐标平面，以测区西南角作为坐标系的原点，以纵坐标轴为x轴，向上(向北)为正；以横坐标轴为y轴，向右(向东)为正；角度(方位角)从x轴正向开始按顺时针方向量取，象限也按逆时针方向编号，以便三角函数公式的应用。

2.2.5 独立坐标系的建立

独立坐标系是相对国家统一坐标系而言的一种近似的国家坐标系，其特点是这种控制网点坐标与国家3°带坐标基本一致，可以通过坐标换算展绘在国家各种基本图上。

1）由高斯平面坐标换算投影高程面上的独立坐标

在有国家控制网的测区，当测区内投影长度变形值大于2.5 km时，为使控制网点坐标尽可能与国家统一坐标接近，可以将多个国家控制网点的高斯平面坐标直接换算为测区投影高程面上的独立坐标，作为起算点进行测量、平差计算。其建立方法是：选取测区内国家3°带的高斯坐标的一点作为独立坐标系原点，另一点作为起算边（起算方位）进行换算。换算公式如下：

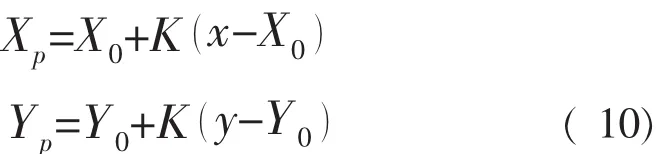
式中：Xp、Yp——独立坐标系坐标；

X0、Y0——独立网原点在3°带的高斯坐标；

x、y——在3°带的高斯坐标；

K——测区平均高程面与高斯平面同名边长度比。K值按下式计算：

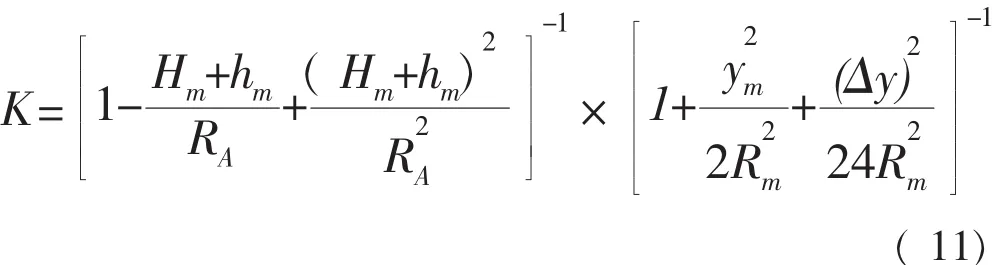
式中：ym——起算边两端点y坐标均值（取自然值）；

Δy——起算边两端点y坐标差；

Hm——测区平均高程面高程；

hm——测区大地水准面相对椭球面的高度（可根据测区大地水准面差距图查出它的概值，无资查取也可略去）；

RA——起算边方向椭球面法截弧的曲率半径，可由下式计算：

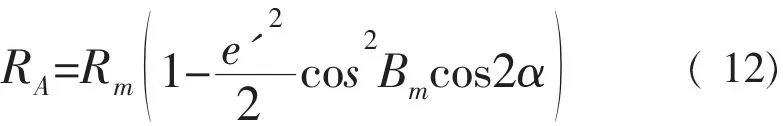
式中：Rm——起算边中点地球半径；

e′——椭圆的第二偏心率；

Bm——起算边中点纬度；

α——起算边方位角。

Rm、e′应当根据所选的坐标系统（1954年北京坐标系、1980年西安坐标系）选取相应的参数。

2）由投影高程面上的独立坐标换算高斯平面坐标

3 结束语

通过上述五种选择局部坐标系统的建立方法可以看出：第一种和第四种使用起来比较简单，但应用范围受到限制；第二种方法是通过变更头面面来抵偿长度综合变形的，具有换算简便、概念直观等优点；第三种方法是通过变更中央子午线、选择任意带来抵偿长度综合变形的，同样具有概念清晰、换算简便的优点，但换系后与原国家同一坐标差异较大。希望广大工程建设者能够根据工程的大小、地形的复杂程度和工程所处的地理位置选择不同坐标系，以减少投影变形的误差，从而达到节省人力、物力，提高施工控制网精度的目的。