一个“隐蔽”的力矩

涂 泓 朱炯明

（上海师范大学数理学院，上海 200234）

在讨论与杆相关的问题时，常常容易遗漏一个“隐蔽”的力矩.这个力矩不易发现，却是普遍存在、不能忽略的.正是由于这个力矩所具有的特点，我们很可能会由于忽略了这个力矩，从而得出错误的、乃至极不合理的结论，却还没有发现.其实，通过仔细的受力分析，还是不难从一些简单的模型中找出这个“隐蔽”的力矩，并且在此基础上研究这个力矩的物理意义，以及它与哪些物理因素有关.

1 横梁中的“隐蔽”力矩

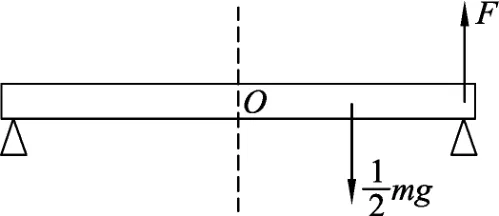
图1

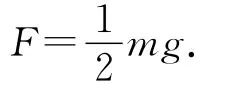
因此横梁所受合力为0.

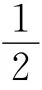
2 “隐蔽”力矩的来源

横梁的右半段除了受到重力和支持力以外，只可能受到来自左半段横梁的力，因此这就是那个“隐蔽”力矩的唯一来源.左半段横梁对右半段横梁所施加的力发生在中间O点处的横截面上，可以将其分解为沿截面方向的横向力T和沿横梁方向的纵向力N，分别加以分析.

2.1 横向力T

根据牛顿第三定律，横截面两侧的横向力T必定大小相等、方向相反.而横梁两侧的情况完全相同，若横截面右侧有一个竖直向上的横向力T提供平衡力矩，那么横截面左侧的横向力必竖直向下，从而使左半段横梁的力矩更不平衡而发生顺时针旋转.这就意味着横截面两侧的横向力T必定都为0.

2.2 纵向力N

既然右半段横梁在O点处的横向力T为0，那么与重力和支持力的合力矩相平衡的“隐蔽”力矩就只能由纵向力N提供.但是如果以为纵向力N通过转动轴，所以力臂为0，从而力矩也为0，因此也不能提供所需的平衡力矩，那就错了.

实际情况是，当横梁被搁置在两个支架上时，会在重力的作用下略向下弯曲.图2中显示了横梁中间一段的情况，靠近上边缘一侧发生压缩形变，而靠近下边缘一侧发生拉伸形变，中性层（图2中用虚线表示）则既不拉伸也不压缩，只是发生形状弯曲.

图2 横梁在重力作用下发生形变

3 “隐蔽”力矩的计算

为了避免不必要的繁复计算，不妨假设横梁的横截面为一矩形，其厚度和高度分别为a和b，并设立坐标系，如图3所示.

图3 横截面右侧部分横梁受力情况

设距离中性层z处宽度为dz的狭条（图3中阴影部分）材料的应变为ε，产生的应力为σ.在发生形变前，dz层与中性层长度相等.形变后的状况如图4所示，假设中间层的曲率半径为R，则dz层的应变为

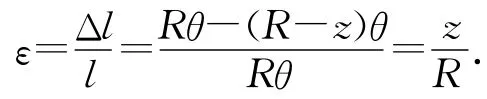
根据胡克定律，在弹性限度内，物体由于形变而产生的应力与其应变成正比，即

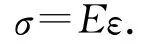
其中的系数E为材料的弹性模量.那么dz层横截面上的应力对右端支点的力矩为

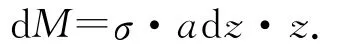
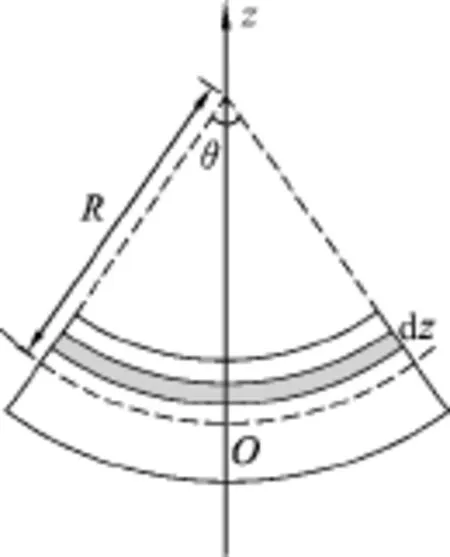
图4 横截面应变计算示意图

整个横截面上的总力偶矩大小相当于自上而下各狭条受到的力矩之和，即

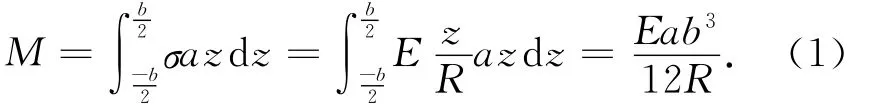
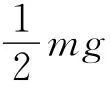
4 “隐蔽”力矩如何使横梁保持平衡

由（1）式可知，沿横梁方向的纵向力所提供的“隐蔽”力偶矩的大小取决于横梁材料的弹性模量E、横梁的厚度a和高度b，以及横梁的弯曲程度（曲率半径R）.但不管横梁是用什么材料制作的，不管横梁的厚度和高度如何，也不管半段横梁对支点的重力矩有多大，这个“隐蔽”的力偶矩总能使右半段横梁保持力矩平衡.其中的奥秘就在于横梁的弯曲程度的“调节功能”.常识告诉我们，对于一根材料弹性模量、厚度和高度都确定的横梁，如果横梁比较重，重力矩就比较大，这时候，横梁会弯曲得比较厉害，或者说曲率半径R比较小，于是力偶矩就会比较大，大到恰好与重力矩平衡.同样，在重量相同的情况下，如果材料比较“软”（弹性模量E比较小），或者比较细（厚度a和高度b比较小），尤其是高度比较小，（1）式中表现为b3，横梁也一定会弯曲得比较厉害，曲率半径比较小，使力偶矩保持不变，能与重力矩平衡.

值得指出的是，如果研究的是一根理想化的均匀细杆，横截面的面积趋于0，是不是那个“隐蔽”力矩就会不存在呢？显然，答案是否定的.从（1）式不难看出，当a，b趋于无穷小时，只要弹性模量E趋于无穷大，力偶矩的大小还是一个确定的量，恰好与重力矩平衡.由此可见，细杆作为一个理想模型，除了要求无穷细，不会弯曲以外，还必须是无穷“硬”的，即它的弹性模量也一定是无穷大的.

5 转动细杆的“隐蔽”力矩

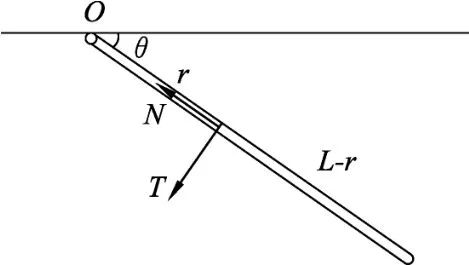
图5

为了说明以上分析中所指出的纵向力产生的力矩是普遍存在的，再给出另一个稍复杂些的例子.2013年第30届全国中学生物理竞赛复赛试卷中的第3题所给的模型为：一质量为m、长为L的匀质细杆，可绕过其一端的光滑水平轴O在竖直平面内自由转动，杆在水平状态由静止开始下摆（图5）.

由此题第1、2小题的答案得出，细杆在下摆过程中的动能可表示为

题目的第3小题要求杆摆至与水平方向成θ角时，在杆上距O点为r处的横截面两侧部分的相互作用力.这一小题用质心运动定理和角动量定理来求解，得到的答案是不同的.

解法1：用质心运动定理解答.

以细杆与地球为系统，下摆过程中机械能守恒，当杆摆至与水平方向成θ角时，动能为

由（2）、（3）式得

以在杆上距O点为r处的横截面外侧长为L-r的那一段细杆为研究对象，该段细杆质量为λ（L－r），其质心速度为

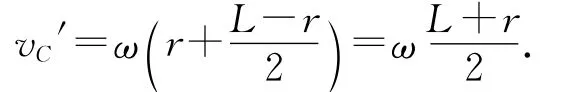
设另一段细杆对该段细杆的横向（即垂直杆方向）力为T（以θ增大的方向为正方向），纵向（即沿杆方向）力为N（以指向O点方向为正向），由质心运动定理得

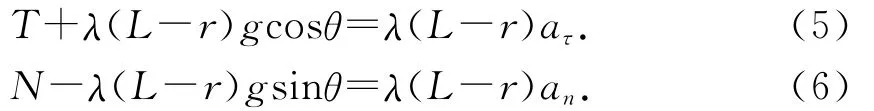
式中aτ为质心的横向加速度，大小为

而an为质心的纵向加速度，大小为

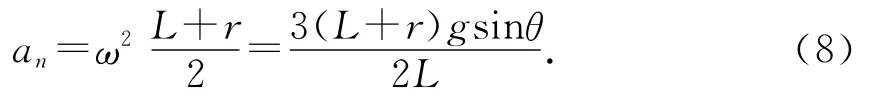
由（5）～（8）式解得

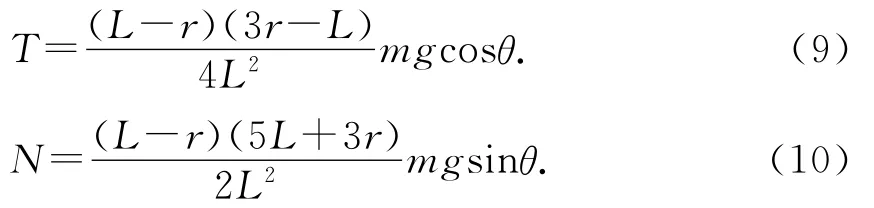
解法2：用角动量定理解答.

以横截面外侧长为L＋r的一段细杆为研究对象，以上方转动轴O为参考点，此时细杆的转动惯量为

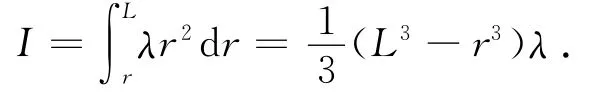
根据角动量定理有

可得

根据（4）式可知

代入（11）式可解得

将（9）式和（13）式相比较可知，两种方法给出的横向力是不同的.结合上文对横梁的分析不难理解，造成这种差异的原因在于，在角动量定理解答的力矩分析过程中，遗漏了细杆中纵向力的“隐蔽”力矩.

为了说明这个纵向力的力矩，先分析一下应力在杆的横截面上的分布情况.题中所求在杆上距O点为r处的横截面外侧长为L－r那一段受力情况如图6所示，将此横截面合理简化为一个矩形.由于杆在重力和转轴O处的支持力的共同作用下产生形变，截面上各处的纵向应力大小是不同的，靠近上边缘的纵向应力较大，向下逐渐减小，并且其大小变化是线性的.

截面中心处的纵向应力为

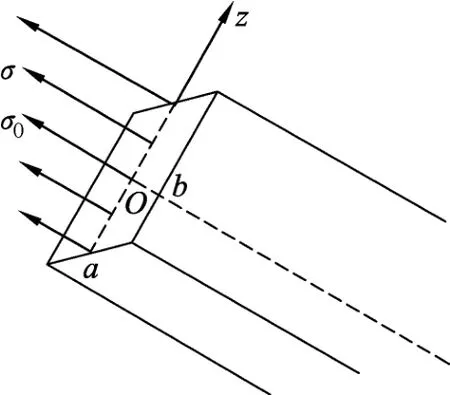
图6 细杆横截面受力情况示意图

这里σ0就是杆所受纵向合力N在整个横截面上的平均力密度，截面其余点处的纵向应力为

其中k为应力在杆横截面上的线性分布系数，相当于应力沿杆横截面的分布梯度.可见σ－σ0在中心线两侧大小相等、方向相反，因此纵向力可以等效看成是由一个均匀分布的力N和一对力偶构成，这对力偶是由于杆的形变引起的，它不改变纵向合力的大小，但会产生力矩

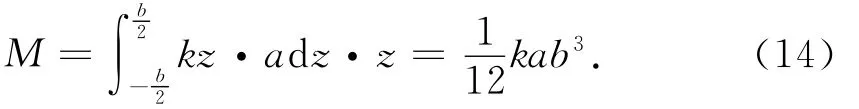
而这个力矩的遗漏就导致了用角动量定理计算的横向力（见（13）式）不正确，因此（13）式与用质心定理计算得到的T的正确值［见（9）式］之间的差值ΔT的力矩为

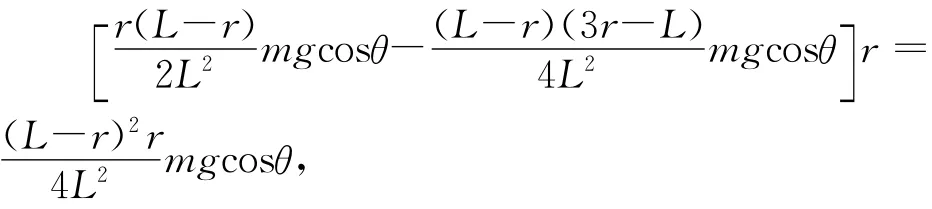
就应该等于（14）式给出的力偶矩，即

（11）式的角动量定理方程，正是缺失了这个力偶矩，从而导致计算出的T不正确.由图6不难看出，这个力偶矩的作用是逆时针的，因此（11）式的正确写法应该是

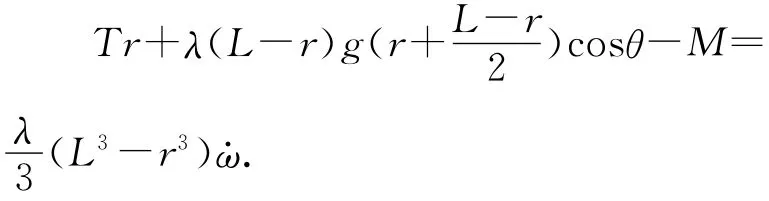
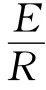
由（15）式第一个等号可见，杆中的力偶矩M的大小与两个变量θ和r有关.也就是说，当杆摆动到各种不同角度时，杆上某处的纵向力力矩的大小是不同的；而当杆摆到某一角度时，杆上各不同位置处的纵向力力矩也是不同的.根据（15）式，可以画出杆中的力偶矩随θ和r变化的图像，分别如图7（a）和（b）所示.图7（a）是在杆上r＝0.3L处的力偶矩随θ的变化情况；图7（b）是当杆摆到θ＝60°处时的力偶矩随r的分布情况.

图7

（2）M是r的3次函数，因此变化情况比较复杂.当杆摆动到某一角度θ时，在杆的两个端点r＝0和r＝L处力偶矩都等于0，这就意味着在杆上某处必定存在着极值.将（15）式第1个等式对r求导并令其等于0，可得

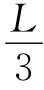
由本文的分析可见，在研究力矩问题时，由于物体形变而产生的应力力矩是普遍存在的.但是这个力矩比较隐蔽，在计算过程中常常会被遗漏，结果就会造成不易发现的错误.而在使用力学问题中常见的细杆模型时，尤其要注意这个问题，不管杆有多细，这个“隐蔽”的力矩都是客观存在的.

1 漆安慎，杜婵英.力学［M］.北京：高等教育出版社，2005：272－274.

2 赵凯华，罗蔚茵.新概念物理教程力学［M］.北京：高等教育出版社，2008.

3 贾玉磊，贾瑞皋.刚体角动量的定义和定义状态量的原则［J］.物理与工程，2008，18（5）：13－16.