孰快孰慢——论2015年高考福建理综卷第17题
欧剑雄
(福建省莆田第一中学,福建 莆田 351100)
1 试题及其引发的争论

图1
题目.如图1,在竖直平面内,滑道ABC关于B点对称,且A、B、C3点在同一水平线上.
若小滑块第1次由A滑到C,所用时间为t1,第2次由C滑到A,所用的时间为t2,小滑块两次的初速度大小相同且运动过程中始终沿着滑道滑行,小滑块与滑道的动摩擦因数恒定,则
(A)t1<t2. (B)t1=t2.
(C)t1>t2. (D)无法比较t1、t2的大小.
本题为2015年高考福建理综卷第17题,参考答案为(A)选项.这道试题一出现,便引发了热烈的讨论.代表性的观点主要有以下两种.
观点1.认为(A)选项正确.持该观点的教师认为,由于AB段为凸曲面,考虑到圆周运动所需的向心力,滑块在该段运动时所受的支持力和摩擦力减小;反之BC段为凹曲面,滑块在该段运动时受到的支持力和摩擦力增大.而滑块从A滑到C时经过AB段任意位置的速率均大于从C滑到A时经过该位置的速率,从A滑到C时经过BC段任意位置的速率均小于从C滑到A时经过该位置的速率.故滑块从A滑到C时经过B点、C点的速率分别大于滑块从C滑到A时经过B点、A点时的速率.由此有两种解法.
解法1:由于滑块从A滑到C时经过B点、C点的速率分别大于滑块从C滑到A时经过B点、A点时的速率,故滑块在AB段的平均速率大于CB段的平均速率,BC段的平均速率大于BA段的平均速率,因此t1<t2,(A)选项正确.
解法2:根据滑块通过A、B、C3点的速率大小关系,结合运动过程的速率-时间图像,可得t1<t2.
观点2.认为(D)选项正确.持该观点的教师认为,仅根据几个点的速度并不能判断物体在整个运动过程中的平均速率.虽然滑块从A滑到C时经过B点大于滑块_从C滑到A时经过B点时的速率.但是,>vCB并不总是成立的.显然,当AB段曲面高度较高,而滑块与滑道间的动摩擦因数较小时,故不能由此得出t1<t2.另一方面,由于滑块的运动较复杂,并不能精确地画出整个运动过程的速率-时间图像,而滑块从A滑到C时是先减速后加速,从C滑到A时是先加速后减速,因此图像法画出来的结果也有可能是t1>t2.而且题目中并未指明曲面为圆弧,要证明在任意曲面下均有t1<t2这在考场上是不可完成的,故答案应该是无法比较t1、t2的大小.
那么上述观点究竟孰是孰非?观点1中的两种解法都是不严谨的,而支持观点2的教师却举不出t1>t2的反例来证明该结论的正确性.要判别两个观点的对错,要么给出t1<t2的严格证明,要么举出t1>t2的反例.为解决上述争论,笔者在此给出“在任意曲面下均有t1<t2”的严格证明,供大家探讨.
2 t1<t2的证明
2.1 3个引论
为了方便后面的叙述,先介绍以下3个引论.
引论1:对于斜面轨道,摩擦力对滑块做功Wf=-μmgcosθ·s=-μmg·x(式中x为滑块运动始末位置的水平距离).
引论2:对于题目所给曲面轨道,滑块从A滑到C的末速度vt1大于滑块从C滑到A的末速度vt2.证明过程详见上文观点1.



2.2 斜面轨道t1<t2的证明
首先证明斜面轨道下,结论t1<t2成立.

如图2所示,在轨道上取两点D、E关于B点对称.滑块从A滑到C过程中经过这两点的速度分别记为vD1和vE1,滑块从C滑到A过程中经过这两点的速度分别记为vD2和vE2.
结合引论1,根据动能定理有
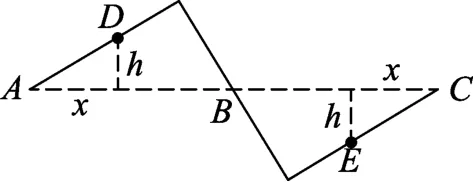
图2

在D点和E点各取一微小位移Δs,则滑块从A滑到C通过这两段微小位移的时间和为
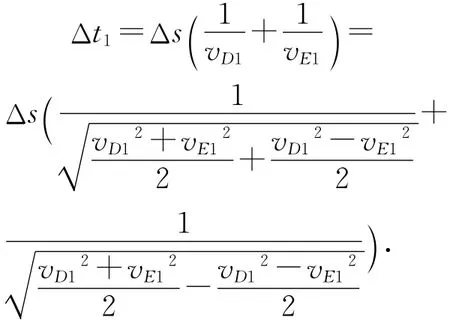
滑块从C滑到A通过这两段微小位移的时间和为

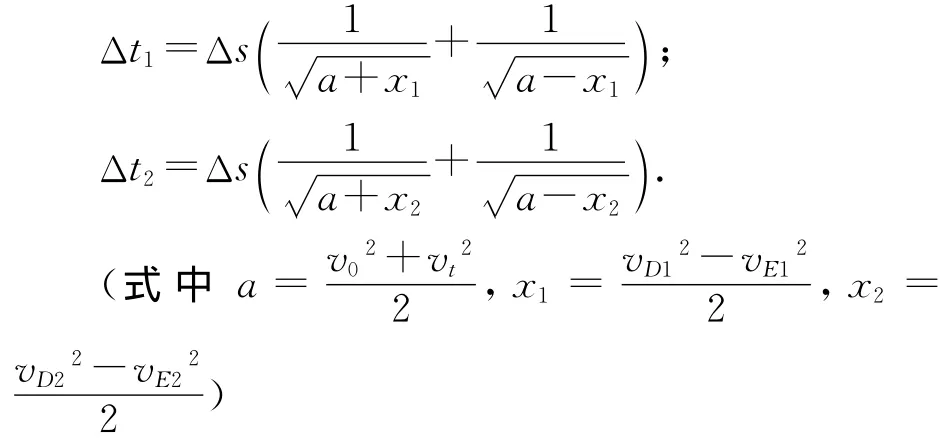
根据引论3可知Δt1<Δt2,故有t1<t2.
(也可根据匀变速直线运动的规律来证明斜面轨道t1<t2,但是这种证明方法数学过程较为繁琐,故本文未给出详细过程,有兴趣的读者可自行证明.)
2.3 曲面轨道t1<t2的证明
再证明任意曲面轨道上,结论t1<t2成立.
轨道AB段为凸曲面,故滑块在轨道AB段运动时,轨道对其的支持力为

轨道BC段为凹曲面,故滑块在轨道BC段运动时,轨道对其的支持力为

我们仍在轨道上取两点D、E关于B点对称,并将滑块从A滑到C过程中经过这两点的速度分别记为vD1′和vE1′,滑块从C滑到A过程中经过这两点的速度分别记为vD2′和vE2′.
考虑到滑块摩擦力的变化,根据动能定理,我们可得到

在D点和E点各取一微小位移Δs,则滑块从A滑到C通过这两段微小位移的时间和为
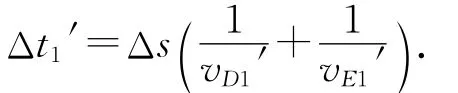
滑块从C滑到A通过这两段微小位移的时间和为
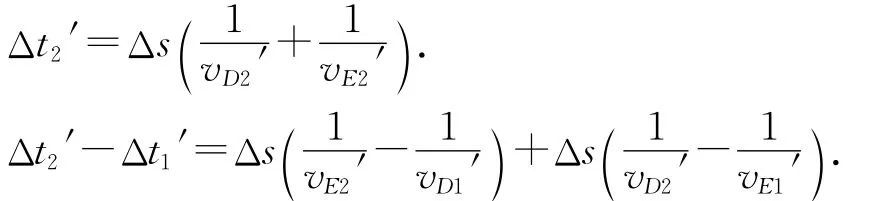
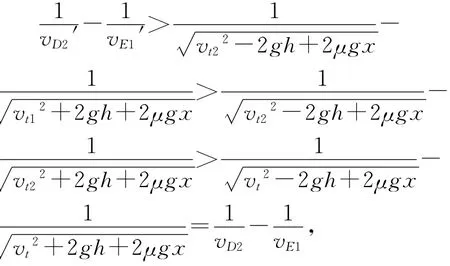
即Δt2′-Δt1′>Δt2-Δt1>0,故有t1′<t2′,结论得证.
3 试题评析
虽然我们能够证明对满足题意的任意曲面均有t1<t2成立,但从上面的证明过程以及笔者对福建省某重点中学理科实验班部分考生的考后访谈来看,本道试题仍存在诸多值得商榷的地方.
3.1 试题难度过大
从上面的证明过程来看,本道试题的绝对难度极大,考生根本不可能按正确的方法做出判断.而选择题这种题型本身存在一定的误差,有一定猜测的概率.[1]选择题难度过大会造成考生放弃思考而凭感觉乱猜,使试题完全丧失考试功能.
在考后访谈中,有50%的考生表示在考场上“无从入手,只能凭感觉猜个答案”.考虑到受访对象整体能力较强(历届该班学生高考总分平均分均在全省前1%),因此实际上所有考生的猜答率肯定远高于此.
3.2 试题效度低
考试的目的是根据考生在考试中的表现推测考生的心理结构或能力,进而预测考生在非考试环境下的表现或行为.[2]对于高考物理而言,我们预测分数高的考生应该具有较强的物理学科能力.效度就是用来衡量这种预测的正确性和有效性的指标.高考作为一种选拔性考试,效度是评价其科学性最为主要的指标.[3]
从考后访谈中的结果来看,除了那些“凭感觉猜答案”的考生外,选择(A)选项的考生的解题过程基本与观点1相同,也就是说思维不严谨的考生反而能答对本题.还有部分考生也想到了观点1的解法,但他们认为此方法只能比较两者末速度的大小,而不能比较两者时间的关系,在花了大量时间不断地尝试其他方法仍不能做出判断之后,就选择了(D)选项,不难看出,这部分考生的思维更加严谨、物理学科能力更强,调查中也发现这部分考生平时的物理成绩均在实验班中名列前茅.也就是说在高分段,这道试题的得分与学生的学科能力呈负相关关系.
基于上述分析,结合文献[4]提出的试题效度理论,笔者认为本道试题为低效度试题,这类试题不宜在高考中出现.
1 教育部考试中心.高考物理测量理论与实践(2007年版)[M].北京:高等教育出版社,2006.
2 雷新勇,周群.试题命制的理论和技术(一)[J].考试研究,2008(4):84-97.
3 吴根洲.高考效度问题研究[D].厦门:厦门大学高等教育学,2007.
4 欧剑雄.高考物理试题效度证据的研究[J].物理通报,2015(7):85-90.

