两个物体的碰撞

宋文斌

（陕西省凤翔县凤翔中学，陕西 凤翔 721400）

1 3类基本问题

1.1 弹性碰撞

质量分别为m1、m2的物体速度分别为v1、v2，碰撞后的速度分别为v1′、v2′，在碰撞的过程中没有能量损失，则同时满足两个守恒，即动量守恒和动能守恒.

解得

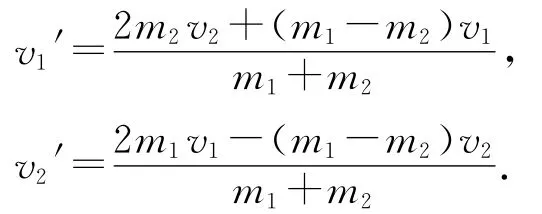
讨论：（1）当v2＝0时，则

这种情况就是常见的一个运动的物体和一个静止的物体发生弹性碰撞的情形.

① 当v2＝0，m1＝m2时，则v1′＝0，v2′＝v1.

这种情况是碰撞后实现了动量和动能的全部交换.

② 当v2＝0，m1≪m2时，则v1′≈－v1，v2′≈0.

这种情况就是一个物体被完全反弹的情形，m2几乎不动，m1按原来大小的速率返回，相当于乒乓球碰到了墙上完全弹回.

③ 当v2＝0，m1≫m2时，则v1′≈v1，v2′≈2v1.

这种情况就是m1的速度几乎没变，m2几乎以2倍m1的速度向前运动.

（2）当v2≠0，m1＝m2时，则v1′＝v2，v2′＝v1.

这种情况就是质量相等的两物体弹性碰撞后速度互换.

（3）设v1－v2为碰撞前的相互接近速度，v1′－v2′为碰撞后的相互分离速度，

则v1－v2＝－（v1′－v2′）.

这个问题可以理解为，在弹性碰撞中，碰撞前两物体是多大的相对速度靠近，碰撞后这两个物体也就是以多大的相对速度分开.

1.2 完全非弹性碰撞

质量分别为m1、m2的物体速度分别为v1、v2，碰撞后粘合在一起速度为v，在这种碰撞中能量的损失最大，损失能量为E，此过程中只有动量守恒.

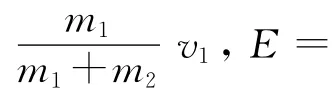
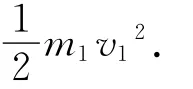
这种情况相当于扔出去的泥巴粘在墙上.

（3）当v2＝0，m1≫m2时，v≈v1，E≈0.这种情况相当于飞行的子弹碰到了尘埃.

1.3 非完全弹性碰撞

在这种碰撞中，碰撞后两物体并没有粘在一起，但是碰撞的过程中仍然有能量的损耗，而能量的损失不是最大的，碰撞的过程中动量依然守恒.

2 两大类基本题型

2.1 判定两个物体碰撞前后运动的情况

这类问题必须要把握碰撞过程中的3个特点.

（1）碰撞的过程动量守恒，p1＋p2＝p1′＋p2′.

（3）碰撞前后物体的速度要符合物理情景.

① 两物体同向运动，碰撞前，追及物体的速度要大于被追及物体的速度；

② 两物体同向运动，碰撞后，追及物体的速度要小于被追及物体的速度；

③如果两物体是相向运动，则碰撞后两物体的速度方向不可能都不改变.

例1.甲乙两球在光滑水平轨道上同向运动，已知它们的动量分别是p甲＝5kg·m/s，p乙＝7kg·m/s，甲追上乙并发生碰撞，碰撞后乙球的动量为p乙′＝10kg·m/s，则2个球的质量关系可能为

（A）m甲＝m乙. （B）2m甲＝m乙.

（C）4m甲＝m乙. （D）6m甲＝m乙.

例2.半径相同的两个小球甲和乙，在光滑的水平面上沿同一直线相向运动，若甲球的质量大于乙球的质量，碰撞前两球的动能相等，则碰撞后两球的运动状态可能为

（A）v甲＝0，v乙≠0.

（B）v甲≠0，v乙＝0.

（C）v甲≠0，v乙≠0.

（D）两球的速度方向均与原来的方向相反，两球的动能仍相等.

例3.光滑水平面上两球沿球心连线的方向以相等的速率相向而行，发生碰撞，以下可能的是

（A）若两球质量相等，碰撞后以相等的速率分开.

（B）若两球质量相等，碰撞后以相等的速率同向运动.

（C）若两球质量不等，碰撞后以相等的速率分开.

（D）若两球质量不等，碰撞后以相等的速率同向运动.

解析：两球相向运动，若质量相等，则两球组成的系统总动量为0，所以选项（B）错误，选项（A）有可能.若两球质量不等，那么碰撞前后系统总动量方向不变，所以选项（C）错误，选项（D）有可能.故选项（A）、（D）正确.

例题4.水平面上，A球以4m/s的速度与静止的B球发生无能量损失的正碰，碰撞后B的速度不可能为

（A）10m/s. （B）8m/s.

（C）6m/s. （D）4m/s.

解析：无能量损失的碰撞为完全弹性碰撞，碰撞前B球速度为0，属于完全弹性碰撞且v2＝0的情况.当两球质量相等时，碰撞以后速度交换，即就是A静止，B的速度为4m/s，与原来A的方向相同；如果A的质量远远小于B的质量，那么A被反向弹回，速度为4m/s，而B几乎静止不动；如果A的质量远远大于B的质量，那么A几乎没有受到影响继续以原来速度前进，而B以原来A速度2倍即8m/s前进.所以B的速度是在0～8m/s之间.故选项（A）正确.

2.2 碰撞过程中的做功和位移计算

对于此类问题的解决，需要在熟练以上内容的基础上更加深刻地理解以下内容.

（1）在碰撞过程中内力做功的效果为以下两方面.

① 有能量损失时内力做功一方面使部分动能在物体间转移，另一方面使部分动能转化为其他形式的能；

② 在没有能量损失时，内力做功只仅使动能在物体间发生转移.

（2）两个物体在碰撞后粘在一起时损失的能量最大，损失的能量为

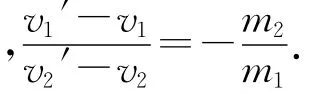
例5.长为l质量为m2的小船静止在静水中，质量为m1的人站在船头，如果不计水的阻力，人从船头走到船尾的过程中，船和人相对水面的位移各是多少？

解析：人和船的运动方向相反，取人的运动方向为正方向.如图1，设人对船的位移大小为l，人对地的位移大小为s1，船对地的位移大小为s2，人对地的速度大小为v1，船对地的速度大小为v2，所以

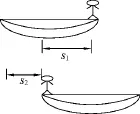
图1

因为人和船运动的时间是相等的，所以

又因为，人对船的位移为

由（5）～（7）式有

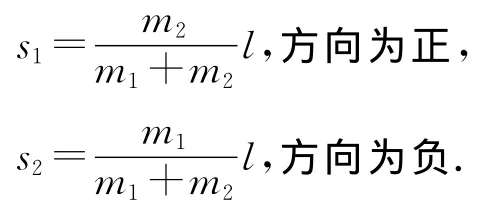
例6.质量为M的长木板在光滑水平面上，一个质量为m的滑块以某一初速度v0沿木板表面从左端滑到右端刚好未掉下来，木板长为l，滑块和木板间的摩擦因数为μ，问：产生的内能是多少？

图2

解析：如图2，该过程相当于完全非弹性碰撞，损耗的能量即就是产生的内能为

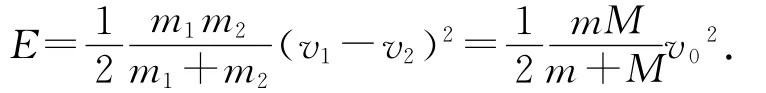
例7.如图3所示，在光滑的水平面上有一个长为L＝1m的小车A，在A上有一木块B（大小不计），A与B质量相等，它们之间的动摩擦因数μ＝0.05.开始时A是静止的，B位于A的正中央且以初速度v＝5.0m/s向右运动.假设B与A的前后两壁碰撞是完全弹性的.问：

图3

（1）B和A发生了多少次碰撞？

（2）B从此位置开始到最终停下来需要多少时间？

解析：（1）设B在A上停下来时B与A的速度相等为v1，由动量守恒定律有

B和A之间的摩擦力为f＝μmg.

由能量转换关系，设B相对A在A上滑行的路程为s，则

由（8）、（9）式解得

解得t＝5s.

1 温应春.“品味”完全弹性碰撞［J］.中学物理教学参考，2007（8）：25－26.

2 刘华.非完全弹性碰撞的一般计算［J］.中学理科：综合，2007（2）：39－40.

3 程旭健.试论弹性碰撞的条件［J］.物理教师，2013（01）：61－62.