对一道物理题目中静态平衡和动态平衡的辨析

王璐珠 郭志君

（湖南师大附中，湖南 长沙 410081）

进入高中阶段物理学习后，学生已能初步建立一些理想模型去分析描述运动的3个物理量——位移、速度和加速度的意义以及它们的相互关系，并能够讨论物体在一定力的作用下如何运动等问题，例如复杂的变加速直线运动、曲线运动等，但有时在分析问题和知识迁移过程中也会存在一些误区.本文通过一道经典例题来阐述静态平衡点和动态平衡点的不同之处.

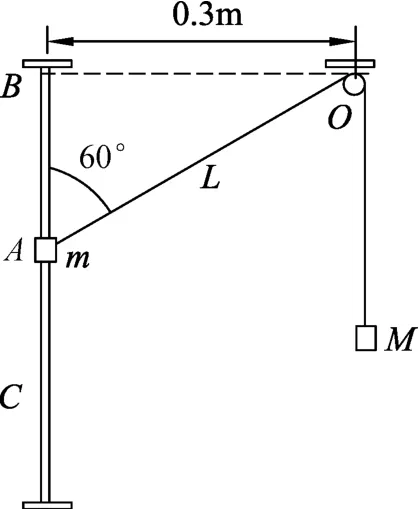
图1

题目.如图1所示，质量为m的物块套在光滑竖直杆上，不可伸长的轻绳跨过固定的光滑小滑轮O（大小不计），小滑轮到杆的水平距离OB＝0.3m.绳的另一端挂一质量为M＝2m的物块，当细绳与竖直杆间的夹角为60°时，系统恰可保持静止状态.不计轻绳的重力和一切阻力（g取10m/s2），当将m由B点起从静止开始释放后，m将在BC间做往复运动，求m的最大速度.

典型错解：由题意知，m在A位置能处于平衡状态，当m从B点静止释放后，经过A位置时合力为0，加速度为0，物块的速度最大.则根据系统机械能守恒有

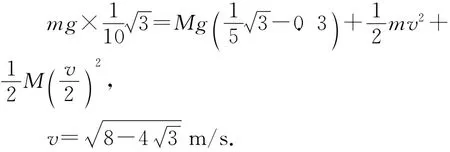
错因分析：做直线运动的物体，经过平衡位置时合力为0，加速度为0，而物体的运动速度最大，这是我们的一个解题思路.在本题中，当系统恰可保持静止状态，是当细绳与竖直杆间的夹角为60°时，即图1中所示A点——静态平衡点，而当m在BC间做往复运动时，A点是否仍是BC间运动过程中的动态平衡点？其实不然，原因在于物体m在往复运动过程中，参与了沿绳方向的运动和绕以滑轮为圆心的圆周运动过程，它的加速度在沿绳方向上应是其向心加速度和物块M的加速度的矢量和，分析过程如下.

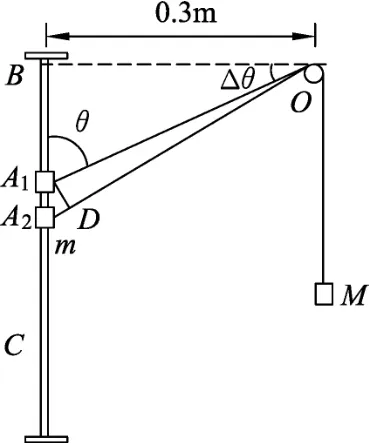
图2

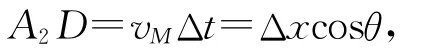
则物块m的速度为

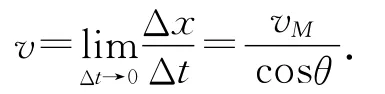
经过一小段时间Δt后，物块M和m速度变为vM′和v′，同理可得

因此在Δt时间内速度的改变量为

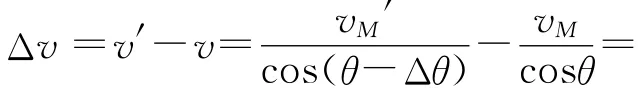
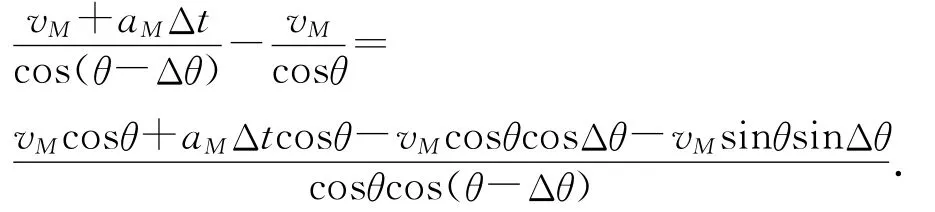
当Δt→0，有Δθ→0，cosΔθ＝1，sinΔθ＝Δθ，因此

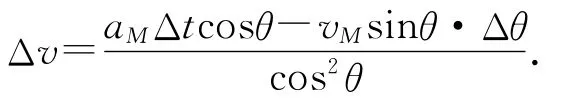
故物块m的加速度为

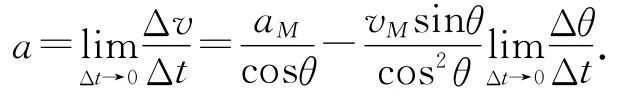
其中

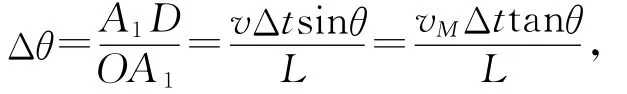
因此

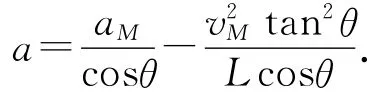
证法2：求导法.如图3所示，x2＋xOB2＝L2，两边分别对时间求导，

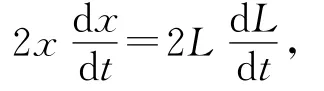
因此

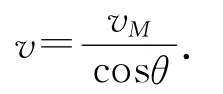
若再对该方程求导可得

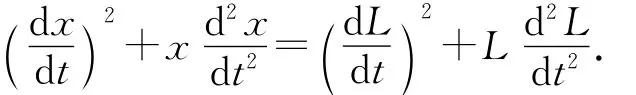
则

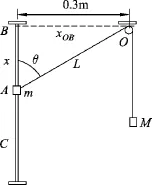
图3

小结：物块m的加速度在沿绳方向上是其向心加速度和物块M的加速度的矢量和.倘若A点是BC运动过程中的动态平衡点，则物块m在A点时加速度a＝0，此时Tcos60°＝mg，再对物块M受力分析得到aM＝0.这显然与实际不符，根据以上分析可知，当物块m的加速度为0时，物块M正处于超重状态，有竖直向上的加速度，因此A点并不是在BC往复运动过程中的动态平衡点.

那么如何求得动态平衡点——最大速度位置？解题过程如下.

解法1：如图4所示，设物块m在E点位置速度最大，此时细绳与竖直杆间的夹角为θ，根据

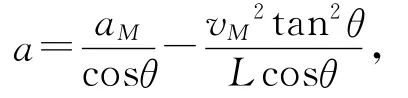
a＝0时有

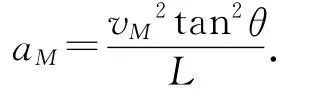
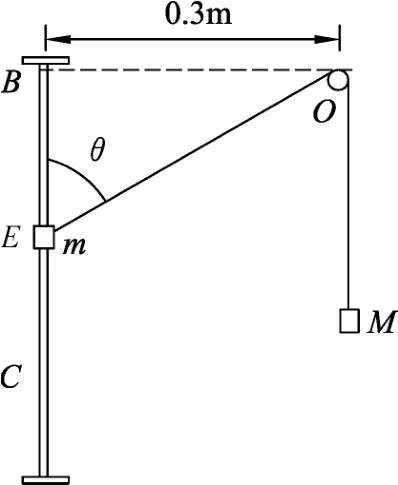
图4

根据牛顿第二定律

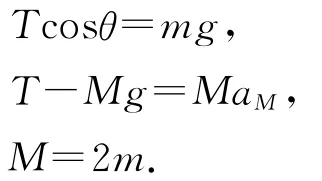
有

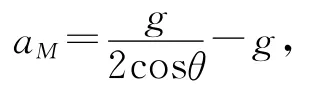
则

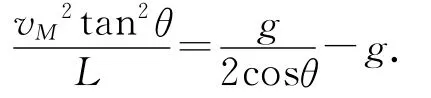
即

根据机械能守恒定律

即

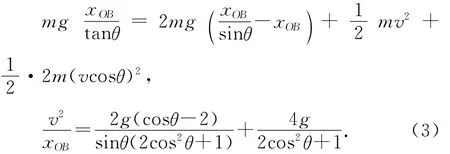
由（1）、（3）式得

解得θ＝67.45°.代入（1）式得v＝1.08m/s.

解法2：直接由机械能守恒定律（2）式得到

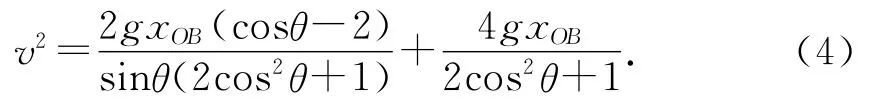
当（v2）′＝0时，v有最大值.同样可解得

θ＝67.45°，v＝1.08m/s.

本文希望这道多本参考资料都曾出现过的物理问题可以给学生带来一些启示，不同问题的形式或内容存在一定的差异性，学生要善于运用已学过的基础知识发现差异，澄清混淆，从而达到从易到难、由浅入深的学习境界.