基于自适应算法的车辆导航路线规划研究

王启明，徐向艺，时合生

基于自适应算法的车辆导航路线规划研究

王启明，徐向艺，时合生

最优路线规划应用到车辆导航系统中时，会导致建模较慢、规划耗时。为了线规划。将自适应遗传算法与贪婪算法相结合，获取最合理的导航优路线规划，能够缩短定位时间，较好的满足了车辆导航系统实时性和实用性的要求。

最优路线规划；车辆导航；自适应算法；最优求解

0 引言

车辆导航系统综合应用了车辆自动定位技术、地理信息系统技术、计算机技术、多媒体技术和现代通信技术等高新技术，它能为车辆驾驶员提供自动车辆定位、路线规划、路线引导、综合信息服务、无线通信等重要功能[1]。最优路线规划是车辆定位导航系统的一个基本应用，要求能够按照电子地图的拓扑信息，帮助车辆驾驶人员或调度人员在车辆出发地和目的地确定的情况下，按照某种策略，如时间最少或路线最短等，实时准确地选定一条最优的行车路线，并显示在计算机屏幕的电子地图上[2]。由于道路环境具有一定的复杂性、多变性，导致传统的车辆导航规划模型具有一定的局限性，降低工作效率。本文提出基于自适应算法的车辆导航路线规划，并对传统算法做了比较深入的探讨，在此基础上构造了新的车辆导航路线规划模型[3-5]。

1 车辆导航路线规划方法原理

车辆导航路线规划过程中，可以将所有的线路作为蜜源构成初始集合，在该集合中，所有的元素都能代表导航线路规划过程中的解，所有的解构成的集合是Yj(1,2,...,n)，采用蜜蜂式搜索方式在类似区域内搜索具有相同属性个体，重复执行搜索模式，以获取最优解[6][7]。

根据公式(1)对所有的导航线路进行实时跟踪监测，并对蜜源更新定位。设置l与k表示随机选取的下标，且具有一定的关联性，当监测系统搜索到车辆导航路线适应性越强，yjk的取值范围越小如公式（1）、（2）：

在车辆导航路线最优解的选取中，利用公式（2）计算具有较强适应性的车辆导航路线占总导航路线的概率。其中，用fitj表示第j个解的适应度值。

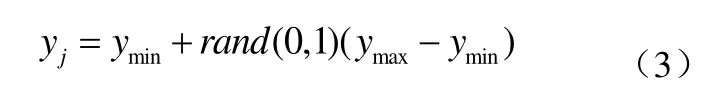
为了车辆导航路线的多样性，利用公式（3）对控制端中具有高强度适应性的车辆导航路线进行变异处理，以便搜索出具有更强适应性的车辆导航路线[8]。具体操作方法如下所述：

（1）采用迭代方法，按照一定规律对旧值变量进行不断递推，进而获取新值。设置蜜源的初始迭代次数用H表示，且H=0，最大迭代次数用Hmax表示，最大限制次数为Limit值。

（2）在蜜源中随机选取n个车辆导航路线，并利用公式（1）计算每个车辆导航路线的适应值，根据每条导航线路的适应性能够判断该解的优越性。

（3）利用公式（2）计算具有较强适应性的车辆导航路线占总逃生路线的概率Qi，根据概率Qi选择最优蜜源，并记录较优蜜源位置，对数据L位置进行实时更新。

（4）在仿真模型中，假如L(j)的值大于最大限制次数Limit的值，在解空间内进一步进行搜索，并记录最优解的位置，保存到监测系统中。

（5）H+1表示在H的基础上进行了一次迭代算法更新，当H大于Hmax值时，记录最优蜜源代表车辆导航路线的最优值。进行第（6）步操作。反之，当H小于Hmax值时，跳转到步骤（3），继续重复操作关于概率Qi的计算。

（6）根据当前车辆导航最优路线规划窗口中的全部导航路线点，在有效的时间内选取越过道路障碍物的最短车辆导航路线，获取车辆导航路线规划。

2 车辆导航最优路线规划方法相关理论

利用传统算法进行车辆导航最优路线规划,建立的规划模型需要满足的约束条件较多，建模耗时较长,降低了规划效率。为此，提出基于自适应算法的车辆导航最优路线规划方法[9][10]。

2.1 搜索车辆导航路线

根据遗传算法对水车辆导航路线进行求解。遗传算法中交叉率QD和变异率QN对车辆导航路线最优解的选取有着决定性的作用，表达式如公式（4）、（5）：

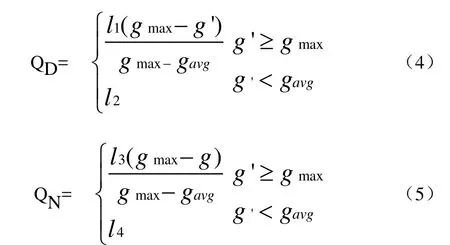
在上述公式中，gmax表示车辆导航路线最大适应度，gavg表示车辆导航路线平均适应度，g'表示参与交叉运算的两个车辆导航路线中较大的适应度，g表示经过变异处理后车辆导航路线的适应度。设置[0,1]，分别表示交叉概率和变异概率的调整参数。在进行交叉运算后保留适应性最强的车辆导航路线最优解。

为了简化运算，提高计算效率，对交叉概率QD和变异概率QN进行优化处理[0,1]，所得公式（6），（7）：

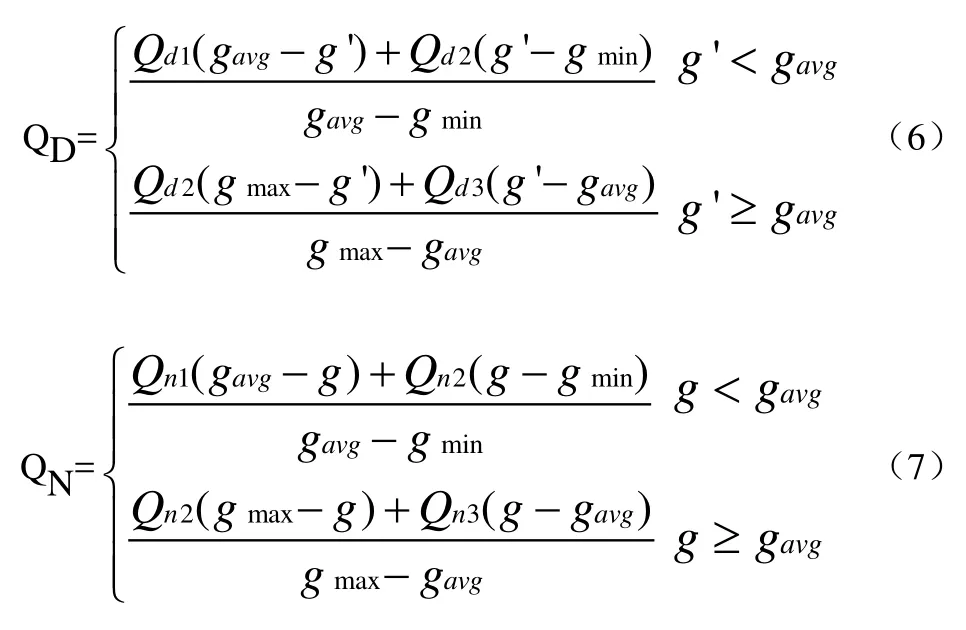
利用上述公式，随机选取两条不同车辆导航路线作为交叉或变异元素，在进行交叉和变异计算时，当两条车辆导航路线中最大的适应度值小于当前导航线路的平均适应度值时，关于导航线路交叉或变异概率的选取，应在最大和最小适应度范围之间进行最优求解，以达到求解标准。

2.2 选取车辆导航最优路线

由于车辆所在的公路环境具有一定的复杂性，导致传统的遗传算法所建立的模拟模型，具有一定的局限性。利用自适应算法优化初始车辆导航路线，可以提高挖掘能力，加快计算的收敛速度。假设有n个有效车辆导航线路规划，利用自适应算法优化初始车辆导航路线的基本思路为：结合车辆所处位置和周围环境以及车流量的大小和方向，随机选取一条最有效的导航路线，设置为1，然后从余下（n-1）条导航线路中寻找最有效的导航路线进行对比。综合各个影响因素，如果第（n-1）条车辆导航路线的适应强度高于第n条车辆导航路线，则用第（n-1）条替代第n条车辆导航路线。将已经作比较的导航线路排除，依次进行对比选择，生成新的个体。

3 实验仿真结果分析

为了验证本文提出的自适应算法的有效性,需要进行一次实验。在实验的过程中，车辆行走的道路和障碍分布情况描述如图1所示：

图1 车辆运行环境模拟

在车辆导航路线规划过程中，车辆的运行速度能够用下图2所示：

图2 车辆运行速度曲线

分别利用传统算法和改进算法进行车辆导航路线规划，获取的规划线路用下述两幅图3图4所示：

图3 传统算法规划结果

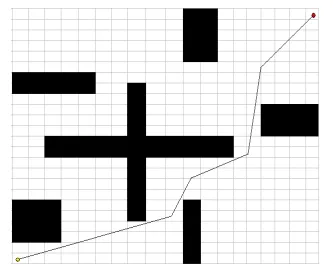
图4 改进算法规划结果

根据图3和图4的对比结果可以得知，传统算法已经陷入到局部最优解，得到的车辆导航线路优越性较差，线路较长，而且没有合理避开障碍。改进算法避免了上述传统算法的缺陷，得到了全局最优解，获取了更加合理的导航线路。在车辆导航路线规划过程中，分别利用传统算法和本文算法进行水下机器人线路规划时，规划线路的协同误差能够用图5所示：

图5 规划线路协同误差

在上述实验过程中，线路规划过程中的误差能够用下图进行描述图图6所示：

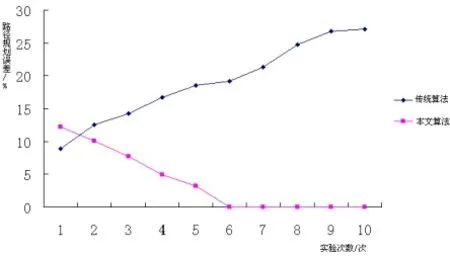
图6 线路规划误差

对上述实验过程中的相关数据进行整理分析，能够得到表1和表2所示：

表1 传统算法实验数据表

表2 改进算法实验数据表

根据上述实验可以得知，利用本文算法进行车辆导航最优路线规划，能够避免传统算法在线路规划方面的缺陷，提高路线选取的合理性，取得了令人满意的结果。

4 总结

本文首先对车辆导航系统进行了研究，针对传统算法无法避免由于建立的规划模型需要满足的约束条件较多造成建模耗时较长的缺陷，提出基于自适应算法的车辆导航最优路线规划方法，并对传统算法和改进算法做了比较深入的探讨，在此基础上构造了新车辆模型。经过分析，采用自适应遗传算法进行车辆导航最优路线规划，选择的导航路线更具有智能性和协调性，解决路线规划这类问题是有实际意义的，它可以较好地满足车辆导航系统实时性的要求。

[1] 孙世博,冯勇,郑剑飞.车辆导航系统最优路线规划研究[J].计算机应用.2006,(09):44-46.

[2] KATRASNIK J,PERNUS F,LIKAR B.A survey of mobile robots for distribution power line inspection[J].IEEE Transactions on Power Delivery,2010,(01):485-493.

[3] WANG Jidai,SUN Aiqin,ZHENG Candong. Research on a new crawler type inspection robot for power transmission lines[C].Piscataway,NJ,USA:IEEE,2010.1-5.

[4] Zhou X F,Guan Y S,Cai C W. Modeling and planning for stable walking of a novel 6-DOF biped robot[C].Piscataway,NJ,USA:IEEE,2010.7-12.

[5] Duan X G,Huang Q,Rahman N. Kinematic modeling of a small mobile robot with multi-locomotion modes[C].Piscataway,NJ,USA:IEEE,2006.5582-5587.

[6] Kanehiro F,Hirukawa H,Kaneko K. Locomotion planning of humanoid robots to pass through narrow spaces[C].Piscataway,NJ,USA:IEEE,2004.604-609.

[7] Chandra Mohan B, Baskaran R. Ant Colony Optimization based recent research and implementation on several engineering domain [J]. Expert Systems with Applications, 2012, 39(4): 4618-4627.

[8] Yeoreum Y,Danielar A. A robot that climbs 3D trusses[J]. Shady3D:IEEE,2007.(03)4071-4076.

[9] 陈立潮.城市交通智能咨询系统的设计与实现[J].计算机工程.2003,29:32-34.

[10] 王凌.智能优化算法及其应用[M].北京:清华大学出版社,2003.

TN393

A

2015.02.10）

1007-757X(2015)07-0041-03

王启明（1980-），男，鲁山人，平顶山学院，计算机科学与技术学院，讲师，硕士，研究方向：软件工程算法和物联网，平顶山，467002

徐向艺（1979-），女，平顶山人，平顶山学院，软件学院，讲师，硕士，研究方向：智能算法、网络安全，平顶山，467002

时合生（1977-），男，郾城县人，平顶山学院，计算机科学与技术学院，讲师，硕士，研究方向：计算机软件与理论，平顶山，467002