DRSS 系统中4+12-APSK信号的应用研究

常海滨

DRSS 系统中4+12-APSK信号的应用研究

常海滨

APSK是一种非常适合于卫星信道的调制方式，它具有较高的功率有效性和频带利用率。在相同功率的情况下具有最大的欧氏距离和高的功率利用率。针对DRSS非线性信道的特性，对16PSK信号、矩形16QAM信号、星型16QAM信号和4+12-APSK信号做出了分析和比较。并仿真比较了几种信号在DRSS非线性信道中的星座图、功率谱和比特误码率并得出结论。证明了4+12-APSK调制信号在DRSS系统中是一种高效的高阶调制方式。

APSK信号；DRSS信道；非线性；仿真

0 引言

随着DRSS系统业务的增加和系统容量的扩展，频谱带宽资源趋于紧张，使用代价也越来越大。为提高频带效益，在信号传输中可考虑采用幅度与相位结合的高阶调制方式。从传统的QPSK升级到8PSK，提高了频带利用率，但其代价是以更高的功率来维持原有的误码性能。高阶正交振幅调制QAM 是可以提高频率利用率，且在相同进制、相同平均发射功率条件下，QAM 比PSK的误码率更低[1]。但是，这类高阶调制方式在卫星信道的应用中，因信号具有多个幅度，通过卫星转发器时，功率效益不高，且存在着对饱和状态放大器引起的非线性失真非常敏感的问题。研究表明，在卫星非线性信道中，16QAM 并不比16PSK系统好[2,3]，且QAM 星座结构往往不适合卫星信道传输，如以等边三角形为基本格状的星座结构，很难满足卫星传输中包络恒定的要求[4,5]。

APSK是一种利用载波幅度和相位同时承载信息的混合调制方式，在同进制和相同误码率下，APSK所需功率要比PSK小[6-7]。特别是在设计适合卫星信道的调制星座时,要求频谱利用率高，尽量减少信号幅度的起伏，这样星座形状呈圆形、圆周个数少的APSK成为极具潜力的一种调制方式。

1 16APSK调制信号

APSK的星座图由K个同心圆组成，每个圆上有等间隔的PSK信号点，根据等效低通原理，每个点都是复值，其信号集为公式（1）：

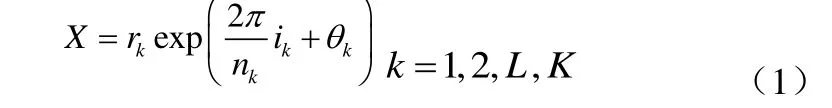
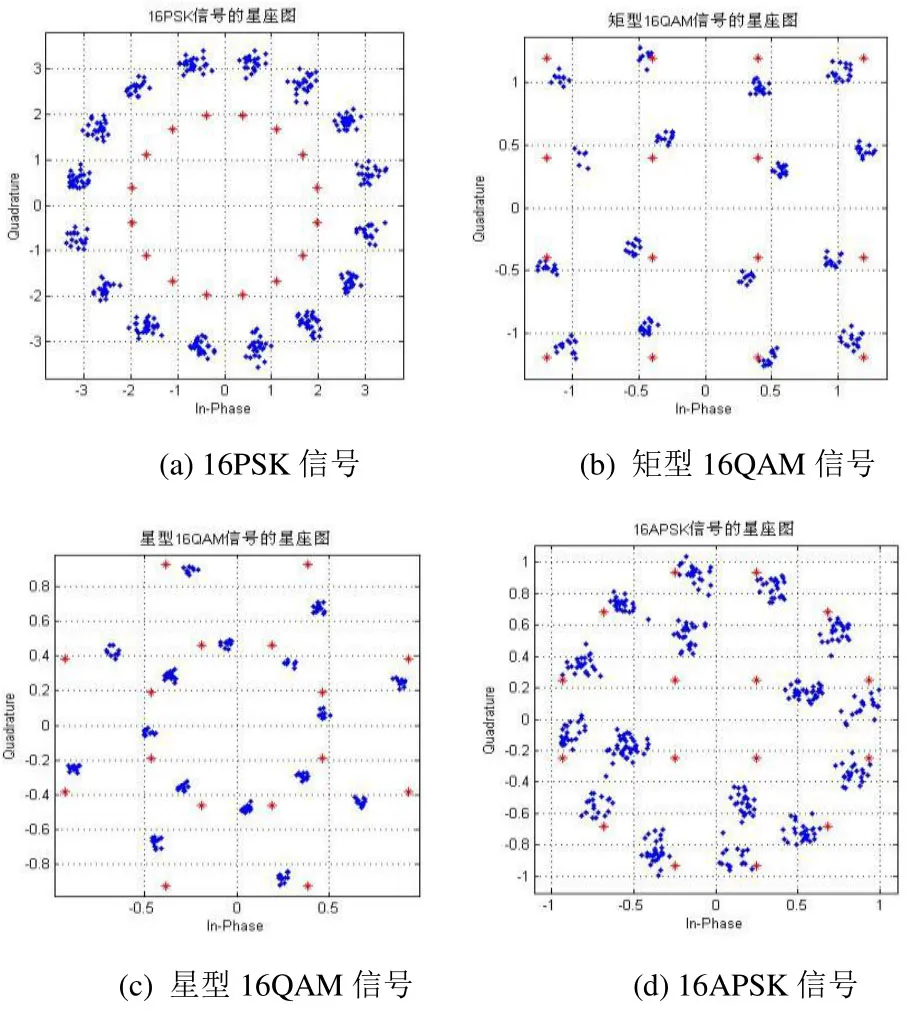
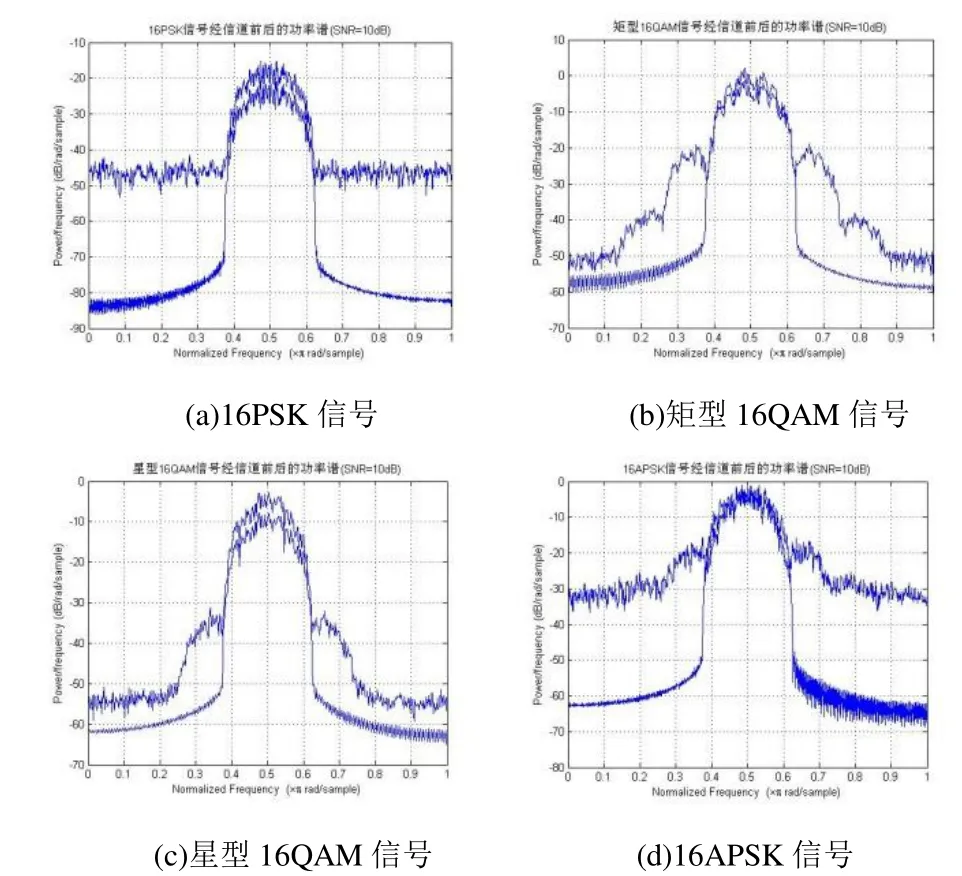
rk为第K个圆周的半径，nk为第K个圆周的信号点数，lk为第K个圆周上的一个点，ik=0,L,nk-1，Qk为第K个圆周上信号点的相位。为了充分利用星座图上的信号空间，应满足nk

16APSK有多种星座图，其中最典型的有4+12-APSK和6+10-APSK，本文所选用的16APSK是4+12-APSK，其星座图，如图1所示：

图1 4+1216APSK星座图

2. DRSS信道模型

研究DRSS URE链路的非线性问题就是研究中继星的非线性问题。DRSS系统中成形滤波和输入滤波都采用平方根升余弦滤波器，虽然成形滤波器在调制信号带宽的同时，在波形信号中引入线性ISI，在AWGN信道下，经接收端的匹配滤波，该ISI得到补偿，平方根升余弦成形滤波＋平方根升余弦匹配滤波＝升余弦滤波，满足奈奎斯特准无ISI则，匹配滤波在抑制信道噪声的同时，起着信道均衡器的作用[8]，如图2所示：

图2 DRSS信道的理想模型

本文选用的DRSS信道模型为Volterra－Wiener模型[9-10]，如图3所示：

图3 扩展Volterra－Wiener模型缺少

将不同阶数的原始信号通过并行滤波器组的输出结果进行相加后，输入到Volterra模型。此模型通过一组简单的线性滤波器，对信号的非线性与记忆深度分别进行了加强，然后，再通过通用Volterra非线性模型，可以适用于任意非线性系统。

3．DRSS系统中的16位调制

在最小欧氏距离都为2a时4种信号所需的平均发射功率如表1所示：

表1 平均发射功率表

即在信号的发射功率一定时4种信号的最小欧氏距离16PSK< 星型16QAM<矩型16QAM<16APSK。

对于DRSS信道HPA进行非线性传输情况下，16APSK比16QAM要好，因为16APSK有更多的信号点处于外圆上，从而进一步提高了HPA的直流转化效率。对于HPA来说，最好能减小内圆信号点数，因为小圆信号点通过HPA是以低功率传送的，降低HPA直流功率转化效率，而HPA的直流转化效率在达到饱和点前是输入功率的单调函数。

在DRSS系统中为了带限，必须对信号进行成形滤波处理，经过成形滤波后的信号幅度为非恒定的，非恒幅信号通过DRSS非线性信道后幅度和相位会随着幅度的变化而发生非线性变化，此变化对系统的性能有很大的影响。

4. 仿真分析

理想的放大器对输入信号的增益是个常数，而实际上并非如此。放大器都有最大的输出功率，当输出功率达到最大后，随着输入信号幅度的增加，其增益会降低，由此引入AM/AM失真[11]。AM/PM失真使放大器的输入输出信号的相位发生变化，AM/PM失真使信号星座点发生了歪斜，歪斜程度取决于输入信号的幅度。幅度越大，失真越厉害。

为了检测各种调制样式对DRSS信道的敏感度，我们在输入信号能量相同的条件下，对16PSK、矩型16QAM、星型16QAM、16APSK经过功率放大器后的性能使用MATLAB软件进行了仿真。

（1）调制信号通过DRSS信道的星座图

调制信号经过DRSS信道后会产生星座点的发散和相位的偏转，如图4所示：

图4调制信号经过DRSS信道前后的星座图

图4是16PSK信号、矩型16QAM信号、星型16QAM信号、16APSK信号通过DRSS信道后的仿真星座图，图中星座点为信号通过匹配滤波器抽样后的信号值，与上面的推导结果相符。仿真所采用的信道模型如图5所示：

图5 调制信号经DRSS信道前后的功率普

参数定义如下：成型滤波器和匹配滤波器都采用具有平方根升余弦滚降特性的系数取0.6,滤波器每符号取个4采样点，抽头数N＝25，即截取峰值点前后各3个符号，输出功率为80W；卫星发射天线和地面接收天线的增益分别为31dB和46.7dB；自由空间路径损耗为－205.4dB。从图4中可看到,调制信号星座点发散，这是由于成形滤波与HPA的记忆效应带来的码间干扰，其结果是导致系统的信噪比降低。

（2）调制信号通过DRSS信道后的功率普密度

信号通过非线性HPA后会发生频谱再生现象，且非线性有记忆效应时载波两边的频谱会发生不平衡现象。下面仿真DRSS信道的非线性对调制信号的PSD（功率谱密度）影响。

图5为16PSK信号在非线性条件下的功率谱密度仿真示意图。图中纵坐标为归一化功率谱密度,单位dB，横坐标为归一化频率。仿真参数定义如下功率谱密度采用周期图估计法，加窗其余各参数的定义同上。

从图5可看出，调制信号通过非线性HPA后功率谱发生了扩展，且载波两边不平衡。这是由于DRSS信道的非线性引起的频率交调互调失真导致的，且此失真与频率有关，其结果是降低了系统的频带利用率。

（3）16PSK通过HPA后的误比特率性能

调制信号在通过DRSS非线性信道后的误比特率性能曲线如图6所示：

图6 调制信号经DRSS信道前后的比特误码率曲线

仿真模仿真参数同图4。

由图6可以看出在DRSS非线性信道，调制信号的误码性能急剧下降，与线性条件下的结果完全不一样了。这是由于HPA非线性的AM/AM转换和AM/PM转换改变了调制信号星座图的最小欧氏距离，这一点在上述的分析中也可明显看出,且仿真曲线与分析的结果基本吻合。

5 总结

由以上的分析和仿真可知：

（1） DRSS系统中相同位数的调制QAM信号优于PSK信号，APSK信号又优于QAM信号。

（2）在DRSS系统中16位调制信号抗非线性性能16PSK< 星型16QAM<矩型16QAM<16APSK。

（3）16APSK调制信号应用在DRSS系统中，有利于充分利用中继卫星的发射功率，节约资源。

（4）在DRSS非线性信道中4+12-APSK信号误码性能最好，抗非线性也最好。

由以上的分析和仿真比较可知4+12-APSK调制信号是一种可以应用在DRSS系统中高效的高阶调制方式。

[1] 达新宇.通信原理教程[M] .北京:北京邮电大学出版社,2005.

[2] LucaGiugno,MarcoLuise, Vincenzo Lottici. Adaptive Pre2and Post2compensation of Nonlinear Distortions for High2level Data Modulations[J ] . IEEE Trans Commun , 2004 ,3 (5) :1492-1495.

[3] EINARSSON G.Signal design for the amplitude2limited Gaussian channel by error bound optimization [J ] IEEE Trans. Commun. , 1979 , 27 (1) : 152-158.

[4] Thomas C M , Weidner M Y, Durrani S H. Digital Amplitude2phase Keying with M2ary Alphabets[J ] . IEEE Trans Commun , 1974 ,22 (2) :168-180.

[5] SHAMAI S , BAR2DAVID I. The capacity of average and peak2power2limited quadrature Gaussian channels[J] IEEE Trans. Inform. Theory , 1995 , 41 ( 7) : 1062-1071.

[6] Biglieri E. High2level Modulation and Coding for Nonlinear Satellite Channels[J ] . IEEE Trans Commun , 1984 ,32 (5) :616-625.

[7] MULL ER M , WACHSMANN U , HUBER J Multilevel coding for peak power limited complex Gaussian channels [ J ] . Proc. IEEE International Symposium on Information Theory ( ISIT’97) . 1997 :627 .

[8] 姜波.中继卫星数据传输系统的载波同步与信道均衡技术研究[D]. 长沙:国防科技大学,2005 年10 月.

[9] Khosrow L., A Nover Volterra-Wiener Model For Equalization of Loudspeaker Distortions[A], ICASSP 2006[C], p:117-120.

[10] PROAKIS J G. Digital communications (fourth edition) [M] . New York : McGraw2Hill , 2001.

[11] SalehA AM.Frequency-Dependent Nonlinear Models and Frequency-Independent of TWT Amplifiers[J]. IEEE Transactions on Communications, 29 (11), November 1981:1523-1528.

TP311

A

2015.03.09）

1007-757X(2015)07-0038-03

常海滨（1981-），男，西安人，陕西学前师范学院，实验室与设备管理处，讲师，硕士，研究方向：卫星通信理论及应用，西安，102072