粒子群算法的改进算法研究

魏晓艳

摘 要： 粒子群优化算法（Particle Swarm Optimization，PSO）是一种高效、动态的优化算法，该算法比较容易实现，也无需调整太多的参数；然而算法后期收敛速度慢，最主要的是易陷入局部极值，为了改善这些缺点，学者们纷纷提出了许多改进的算法，并将其已经应用于科学和工程等多个领域。本文主要是在基本PSO的基础上进行改进，提出了一种新的改进算法—LPSO。最后通过仿真实验证实，改进后的算法在收敛速度和收敛精度上都得到了很大提高。

关键词：粒子群 自适应 早熟收敛 交叉操作

中图分类号： TP301.6 文献标识码：A 文章编号1672-3791（2015）06（a）-0000-00

Research on improved algorithm of particle swarm optimization

WEI Xiaoyan

（School of Engineering， Xi'an Siyuan University， Xian 710038，china）

Abstract： Basic PSO is an efficient and dynamic optimization algorithm， it is easy to achieve and don't need too much parameters adjustment； however， it has slow convergence， easily failing to local extreme values， in order to improve these disadvantages， some scholars have put forward a lot of improved PSO. In this paper， we introduce an improved PSO， and then prove it effective .

Key words： PSO； adaptation； Local convergence； crossover operation；

1 引言

在现实生活中，无论从事什么样的职业，都会遇到优化问题。随着科技的不断发展、世界的不断变化，早前一些静态的、传统的方法，如单纯形法、共轭梯度法、模式搜索法以及牛顿法等，已经不能够很好的处理一些复杂的问题，于是动态的、高效的粒子群算法（PSO）便成为了众多学者研究的热点【1】。

基本PSO算法虽然比较简单，实现相对容易，不需要调整太多的参数，同时算法的早期收敛速度也比较快；但算法后期会受到随机振荡现象的影响，导致算法搜索到全局最优解的时间比较长，减慢

了收敛速度；并且在一定程度上使其局部搜索能力表现较差，极易陷入局部最小值，精度降低，易发

散【2】。针对基本粒子群算法的收敛精度问题，本文提出了一种新的改进粒子群优化算法—LPSO。

2 改进PSO算法研究

2.1 基本PSO算法

随机初始一群粒子，每个粒子均不包括体积和质量信息，将每个粒子都看作为优化过程中的一个可行解，粒子的好坏通过一个事先设定好的适应度函数来进行确定。优化过程中，每个粒子都将在可行解空间中进行运动，由一个速度变量决定其方向和距离。通常情况下粒子将追随当前的最优粒子，并经过不断的迭代搜索最后得到全局最优解。在每一次迭代过程中，粒子都将会跟踪两个最优值：一个是粒子本身迄今为止找到的最优解，即局部最优解；另一个是整个粒子群体到目前为止找到的最优解，即全局最优解【3】。

假设一个由个粒子组成的粒子种群在维的

搜索空间中按照一定的速度进行飞行。粒子在时刻的状态属性设置如下：

位置：

其中为搜索空间的下限，为搜索空间的上限；

速度：

其中：为最小速度，为最大速度；

个体最优值位置：

全局最优值位置：

其中：，。

那么粒子在t+1时刻的位置可以通过下式来得到：

（1）

式中，、都为均匀分布在（0，1）区间的随机数；、是学习因子，一般取2。

基本的PSO算法尽管比较简单，实现也相对容易，并且不需要调整太多的参数，早期收敛速度快；但同时也存在其局限性，由于粒子在移动时没有选择性，即使下一个粒子位置的评价函数值较差，粒子还是利用逐个位置来代替当前位置，这样就使得粒子很容易跳出最优解附近的某一邻域，因此在一定程度上表现出较差的局部搜索能力，比较容易陷入局部最小值，降低了精度，也易发散【4】。鉴于基本粒子群算法还存在一些不足之处，本文提出了一种新的改进的粒子群算法，下面将对其做具体介绍。

2.2 粒子群算法的改进算法研究

本文所提出的改进的粒子群算法主要是在基本粒子群算法基础上，对以下几个方面做了改进：

1）惯性权重模型

由于惯性权重较大时，算法具有较强的全局搜索能力；较小时，则算法局部搜索能力较强。所以本文中采用线性模型，随着迭代次数的增加，将由初始的0.9线性递减至0.4，以达到期望的优化目的。权重函数由下式确定：

（2）

式中为最大惯性权重，一般取0.9，为最小惯性权重，一般取0.4。

2）学习因子模型

学习因子、表示粒子向个体最优值和全局最优值进化的随机加速权值。当、都等于0时，粒子会按照当前速度进行飞行，直到运动至边界处。当学习因子较小时，粒子将会在远离最优值区域内发生振荡现象；较大的学习因子则可以促使粒子快速向最优解区域内移动。所以本文中采用自适应模型，如下式所示：

（3）

式中为最大学习因子， 为最小学习因子，为最大迭代次数，t为当前迭代次数。

3）粒子位置更新方程的改进

基本PSO算法前期，精度较低，易发散。如果参数较大的话，在后期收敛速度会变慢，从而无法继续进行优化。在进化规划中，算法中若带有高斯变异和柯西变异算子时，算法都会取得较好的收敛效果，因此，本文中对个体最优解加入了高斯算子，每次找到一个个体最优值时，将在其周围利用高斯算子进行局部搜索。这样不仅可以提高算法前期的收敛精度，还可以改进算法后期的收敛速度，可以有效避免后期在最优解附近发生振荡。所以本文中的粒子位置通过下式来进行更新：

（4）

式中，是均值为0，方差为1的高斯变量，是个粒子中的最小适应函数值，即当前最优值，是尺度因子，通常取0.6。

4）早熟收敛的改进策略

PSO运行过程中，如果其中一个粒子发现一个当前最优位置，此时其他的粒子会快速向其聚集。如果该最优位置是个局部极值点，或者两个粒子均处于局部极值点，此时整个粒子种群将不可能在解空间内重新进行寻优，导致算法失去了搜索能力，陷入局部最优，这一现象就称为早熟收敛。本文对会与当前最优解重叠的粒子加入交叉操作过程，这样可以使该粒子状态重新更新，寻找新的搜索区域，从而跳出函数的局部极值点。首先给定一个阈值，如果其中一个粒子与当前最优粒子的位置距离小于之前设定的阈值，则对其进行交叉操作。具体的交叉公式如下：

（5）

式中 是粒子位置，为粒子速度，是介于[0，1]之间的一个随机数，为局部最优解。

3 仿真实验

1）粒子群算法性能比较仿真

为了验证改进粒子群算法的有效性，本文中选取标准的测试函数，分别利用基本粒子群算法和改进后的粒子群算法对函数进行优化，寻找适应度函数的最优解。

测试函数：Griewank函数

（6）

式（6）中的表示一个粒子，为粒子的每个分量，为每个粒子的维数【3】。

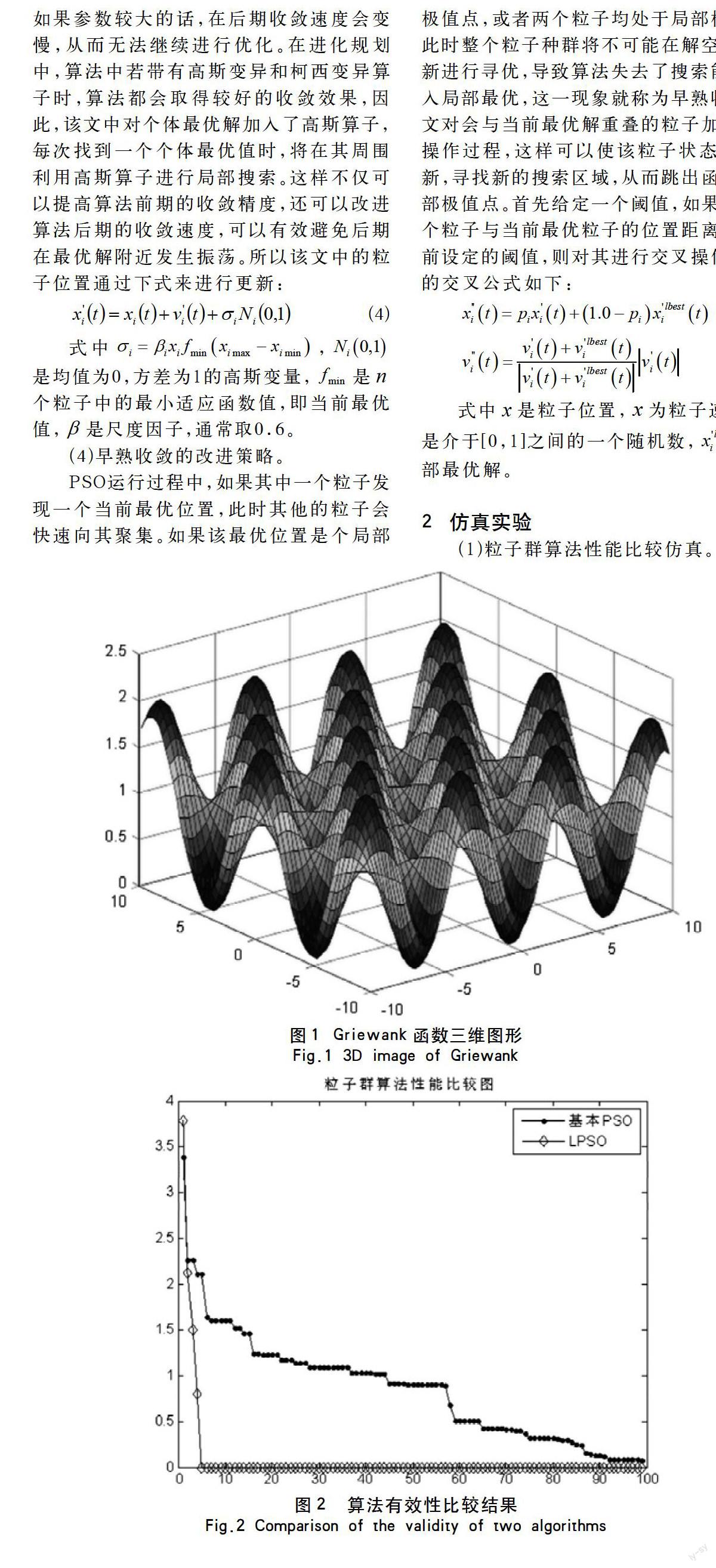
首先在 [-10，10] 的区间内均匀生成两组数，作为初始的粒子种群，数的个数为生成粒子的个数，每个粒子都是二维的，则该函数的三维图形如图1所示。由图可以看出：该函数存在多个局部极值点，但只存在唯一的全局最优点在（0，0）处。

图1 Griewank函数三维图形

Fig.1 3D image of Griewank

本文在进行仿真实验过程中的相关参数设置如下：学习因子，，粒子个数n=100，粒子维数D=10，粒子位置范围，最大迭代次数选取为100次，交叉操作过程中的阈值g取0.5，尺度因子取0.6。仿真结果如下，图中描述的是函数的最优适应值与迭代次数之间的关系。

图2 算法有效性比较结果

Fig.2 Comparison of the validity of two algorithms

由上述仿真结果可以看出，改进的粒子群算法（LPSO）较基本粒子群算法，不管是收敛精度还是循环迭代次数，都有所提高，验证了改进算法的有效性。

4 结论

本文在基本PSO的基础上，对参数的选择进行了调整，同时引入高斯算子及交叉操作过程。仿真结果证明，改进后的算法收敛效果较好。

参考文献

[1]. 张必兰. 改进的粒子群优化算法及应用研究[D].重庆大学，硕士学位论文， 2007.

[2]. 李丽，牛奔. 粒子群优化算法[M].北京：冶金工业出版社，2009.

[3]. 吴进华，吴华丽，周仕. 基于模拟退火的粒子群算法[J].仪器仪表学报，2008.

[4]. Yumao Li. Particle swarm optimization algorithm research and improvement [D]. Northwestern university master degree thesis，2009.

[5]. 任小波，杨忠秀. 一种动态扩散粒子群算法[D].宁夏工程学院，2010-01.

[6]. 刘逸. 粒子群优化算法的改进及应用研究[D]西安电子科技大学，博士学位论文， 2013.