MIMO系统下低复杂度树形检测算法的研究

李扬 金小萍 苏春燕

摘 要：如今移动通信业务对高速度高精度的通信数据传输的要求，促进了学者们对各类通信数据信息检测算法的研究。本文从整体上介绍了各类树形搜索策略的检测思想及其代表算法，按照树形搜索策略的不同分成穷搜索，深度优先搜索，宽度优先搜索和度量值优先搜索四类，列举了各类搜索策略的典型算法，分析了它们的优势和缺点，列举出针对这些缺点拓展出的研究现状，并对现状和问题进行总结，提出了在后续针对树形检测算法进一步优化的研究方向。

关键词：低复杂度，树形搜索策略，树形检测算法

中图分类号：TN911 文献标识码：A 文章编号：1672-3791（2015）06（a）-0000-00

1、引言

现如今，消费者们对移动通信业务的使用已经不仅仅满足于对语音业务的需求，对互联网，多媒体以及视屏通话等业务的需求变得与日俱增。基于此目前正在研究当前和下一代的移动通信，即B3G、4G、5G等系统的关键技术。其中MIMO（多输入多输出）是提高系统传输效率的关键技术之一，已被广泛应用于各个系统当中。而低复杂度的检测技术是MIMO系统核心技术之一，成为近几年学者们研究的一个重点。本文就针对这些研究，将诸多的检测算法进行分类和介绍，并主要针对树形检测算法思想进行阐述，分析其优劣势，在各类算法之间进行多维度的对比，提出未来针对树形检测算法的研究方向。

2、树形搜索思想

在各类的检测算法中，通常按照处理方式的不同将检测方式分为线性和非线性，其中线性检测算法计算原理简单，但是检测译码性能较差。而非线性检测算法中，最大似然算法（ML）属于性能最优的算法，但是过高的计算复杂度问题使得该算法很难在实际中应用，进而提出了诸如深度优先，宽度优先，度量值优先等一系列拥有较低复杂度的性能次优的检测算法。

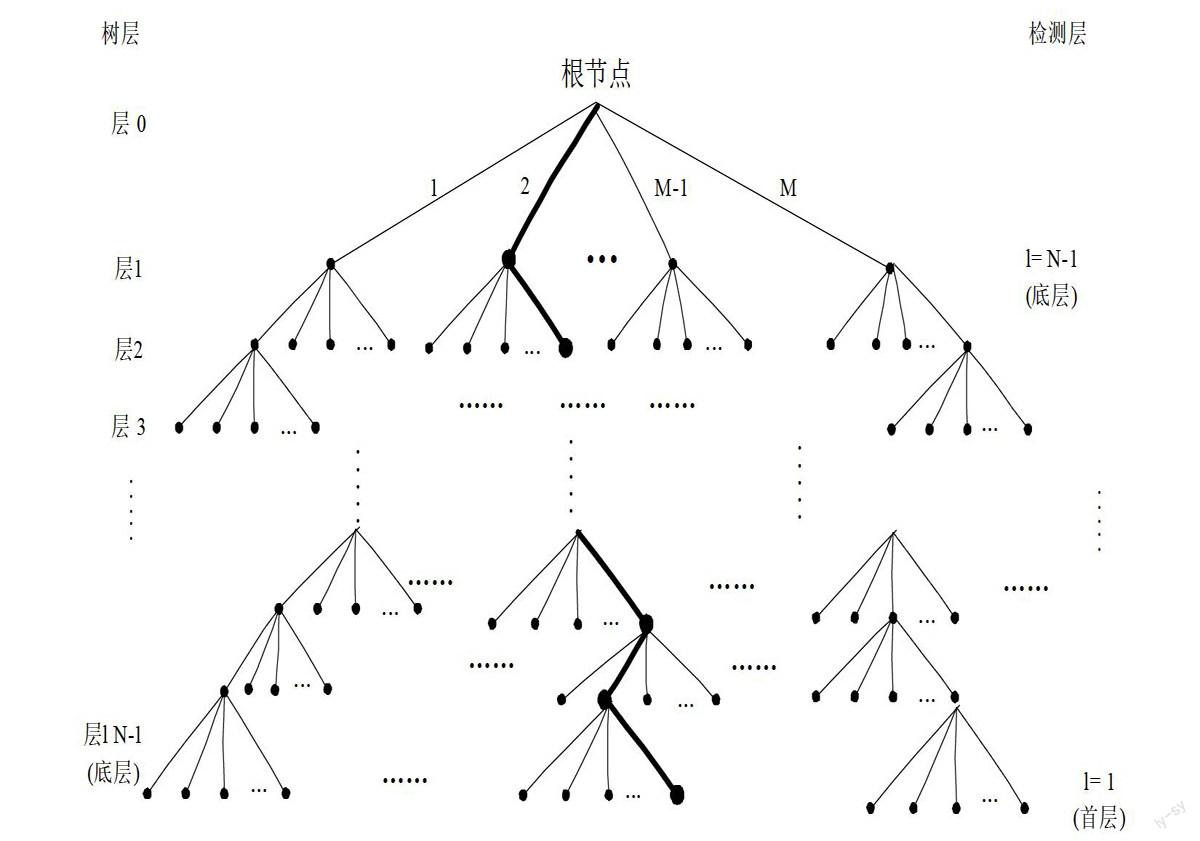
经研究发现，在这些非线性检测算法中有一个共性，就是可以用树的模型来诠释它们的思想，如图1所示，图中M表示采取的调制阶数，根节点表示搜索起始节点，各分支节点表示调制星座点。多天线信道模型通过QR分解等数学推导，可以将接收端检测判决公式的抽象表达式转化成上三角矩阵的形式，然后通过树枝长短来表示度量值的大小，树的层数表示搜索的顺序，树的节点数表示复杂度等，从而将上述各种检测算法问题提炼成树形检测算法的问题来研究。因此将多天线系统各种检测算法的研究，统一到树形检测算法的研究上来，能更好的改进或者设计新的低复杂度检测算法；也为多天线系统在未来先进通信系统的使用，以及硬件实现等方面提供一个更易实现的途径。因此研究低复杂度树形检测算法具有重要的理论意义和工程应用价值。

图1树形检测过程模型图

3、树形检测算法

出于对现有检测算法转化成树形检测算法思想的考虑，将现有算法根据节点选择方式的不同，归类搜索顺序和树枝裁剪两大类，不同的搜索顺序和裁剪方法都会造成不同的性能和复杂度。因此对树形检测算法的研究，能很好实现两方面的平衡。

3.1、搜索策略

根据目前对于树形检测算法的研究结果，可以将它们按照不同的树形搜索策略，分为以下四类：第一类是穷搜索策略，典型的代表为ML检测算法，该算法搜索对比所有的分支，所以在译码性能上是最好的，但是穷搜索也意味着大量的计算量，使其很难在实际中应用；第二类是深度优先的树形检测策略[1-2]，此类算法首先沿着树检测层的深度方向进行搜索，一直到找到一条完整的分支路径，然后再返回访问之前一层的树检测层中的其他分支节点，完成其它分支路径的检测。该算法的译码性能接近ML算法，但是不断进行的返溯运算使其在复杂度上并没有太多的优势；第三类是度量值优先的树形检测策略[3-5]，优先对各分支节点中度量值最小的节点进行搜索访问，在复杂度的降低方面有着较为明显的优势，但是依然需要在各树层之间进行多次的返溯运算；第四类是宽度优先的树形检测策略[5-8]，如宽度优先球形译码算法，K-best算法[5]，BID算法[6-7]，M-BID算法[8]等，此类算法通过固定的半径宽度来限制每层被搜索到的分支节点数目，该算法具有较为稳定的吞吐量，但也可能会带来最佳分支路径的分支节点被删除的情况，造成译码错误。

3.2、树枝的裁剪

关于树枝的裁剪，通常采用的方法是利用半径和概率的限制来进行裁剪。这类树枝裁减思想在球形译码中较为常见，目前存在两个著名的策略：基于噪声统计的半径选择[7-8]，这是个固定半径选择方法，不够灵活；在任意大的初始半径的基础上动态调整半径，这种方法目前使用的比较多，但缺点是半径过于松散，特别在低信噪比下网格点很密集的场合。对此W. Zhao[9]进行了改进，通过在搜索失败时重复计算不完全树的平均路径度量值信息，来找到最有可能的路径。文献[10]中提出了IRA算法，在树的每一层增加了一个概率的限制。然而这种删除会使得在低层的半径限制下出现无解的情况。对此文献[11]提出了基于概率树形裁剪的球形译码，它通过在球形限制的基础上再增加了噪声概率的限制，并结合动态半径调整，以便进一步减少计算复杂度[12]。文献[13]中提出一种基于概率分布的裁剪算法（SPSD），能在不同的网络结构中得到普遍应用，并且引申出的五种裁剪算法均能在复杂度与性能相较传统算法得到明显的改善。

通过对研究现状的分析得知，目前针对树形检测的研究主要集中在复杂度、性能、搜索速度等方面的优化上，不同的搜索和裁减策略通过节点的搜索顺序、半径和概率的限制等多种方式来达到降低算法复杂度，提升译码性能的目的，而且也获得了很多研究成果，但是还存在着以下问题：

1）结合概率思想的算法不够丰富。由现状分析得出，结合概率思想的多为球形译码算法，体现在对半径的设定和半径内节点的筛选上，与其他搜索策略的结合略少。因此，将概率思想引入到更多的树形搜索策略中可以作为未来研究的重要方向之一。

2）在树形的裁剪算法中，主要针对的是深度优先的检测方法，而如何将这种思想运用于宽度优先和度量值优先的检测算法中，并且把算法进行一般化，还没有很好的研究。

3）当前大多性能优良的算法都是基于已知信道信息基础上的，如何把这种思想进行提炼，运用到未知信道信息的多天线系统中，进一步加深和拓展树形检测算法的研究。

4、总结

本文从检测背景，策略，算法以及存在问题等多个方面详细的介绍了树形检测算法，罗列了多种先进的低复杂度树形检测算的优缺点，并针对研究中还存在的问题提出了3点需要进一步进行研究的方向，为低复杂度树形检测算法的研究提供了必要的资料。

参考文献

[1]Jaeseok Lee， Byonghyo Shim. Soft Output list sphere detection with a probabilistic radius tightening[J]. IEEE Transactions on Wireless Commun.， 2008， 11（8）： 2848-2857.

[2]Volker Pauli， Lutz Lampe. Multiple Symbol differential sphere decoding for unitary space-time modulation[J]. IEEE Globecom， 2005， 3： 1630-1635.

[3]李颖， 魏急波， 王欣等. 酉空时调制系统中基于球形译码的多符号差分检测算法[J]. 中国科学（信息科学）， 2009， 39（5）： 569-578.

[4]Peng Li. Adaptive decision-feedback detection with constellation constraints for MIMO systems[J]. IEEE Transactions on Vehicular Technology， 2012， 61（2）： 853-859.

[5]Ran Xu， Kocak T. High throughput parallel Fano decoding[J]. IEEE Transactions on Communications， 2011， 59（9）： 2394-2405.

[6]Tae-Hwan Kim， In-Cheol Park. Small-area and low-energy K-Best MIMO detector using relaxed tree expansion and early forwarding[J]. IEEE Transactions on Circuits and Systems I： Regular Papers， 2010， 57（10）： 2753-2761.

[7]Tao Cui， Chinthananda Tellambura. Bound-intersection detection for multiple symbol differential unitary space time modulation[J]. IEEE TRANSACTIONS COMMUN， 2005， 53（12）： 2114-2123.

[8]N Jin， X P Jin， Y G Ying. Multiple-symbol M-bound intersection detector for differential unitary space-time modulation[J]. IET Communications， 2010， 4（16）： 1987-1997.

[9]W Zhao， G B Giannakis. Sphere decoding algorithms with improved radius search[J]. IEEE Trans. Communications， 2005， 53（7）： 1104-1109.

[10]R Gowaikar， B Hassibi. Statistical pruning for near-maximum likelihood decoding[J]. IEEE Trans. Signal Process， 2007， 55（6）： 2661-2675.

[11]B Shim， I Kang. Sphere decoding with a probabilistic tree pruning[J]. IEEE Trans. Signal Process， 2008， 56（10）： 4867-4878.

[12]B Shim， I Kang. On further reduction of complexity in tree pruning based sphere search[J]. IEEE Trans. Communications， 2010， 58（2）： 417-422.

[13]Tao Cui， Shuangshuang Han， Chintha Tellambura. Probability- distribution based node pruning for sphere decoding[J]. IEEE Transactions on Vehicular Technology， 2013， 62（4）： 1586-1596.