马克思扩大再生产公式的图解法

陶为群

马克思扩大再生产公式的图解法

陶为群

［摘要］基于马克思扩大再生产公式中具有的两个部类不变资本积累变量，提出马克思扩大再生产公式的图解法，可以直观、简便地获得扩大再生产公式的解，以把握怎样求解一般的扩大再生产问题，特别是可以直观地发现和认识马克思扩大再生产公式有解的充分必要条件。

［关键词］马克思；扩大再生产公式；资本积累均衡；图解法

马克思的社会再生产理论以两大部类社会再生产公式集中体现，当且仅当马克思扩大再生产公式有解的情形下，这个公式对于研究现实的国民经济增长具有重要的理论指导意义。因为获得扩大再生产公式的一组解，就是确定扩大再生产的一种具体安排。本文提出马克思扩大再生产公式的图解法，可以直观、简便地获得扩大再生产公式的解，以帮助把握已经有研究给出的求解扩大再生产问题的一般方法（陶为群，2014），[1]特别是可以直观地发现和认识马克思扩大再生产公式有解的充分必要条件。

一、社会再生产的两个部类资本积累均衡方程

马克思社会再生产理论以两大部类社会再生产公式集中体现。社会再生产公式是表示了社会再生产中生产资料、消费资料两个部类的产品价值构成和实物构成，以及生产资料、消费资料的总供给与需求均衡的一组等式。从不同作用的区别来看，这组等式包括了定义方程、行为方程和均衡条件三种类型的方程。按照马克思社会再生产理论，社会生产部门划分为生产资料、消费资料的两个部类，分别记为第Ⅰ、Ⅱ部类。第j部类（j=Ⅰ，Ⅱ。下同）在t年初时点的总资本分解成用于购买生产资料的不变资本、购买劳动力的可变资本两个部分，分别记为Cj(t)，Vj(t)。按照经典的马克思再生产公式中的假定，设Cj(t)和Vj(t)都是每年周转一次；那么，当年Cj(t)作为中间消耗转移到产品当中，Vj(t)在产品当中新创造出来，并带来它的剩余价值Mj(t)。社会产品的价值中包含了由生产资料消耗转移的价值、重新生产出的劳动力的价值，分别与不变资本的转移、可变资本的再生产对应，这两者之间的对比关系由生产力的技术构成决定，并且反映了生产力技术构成的两种属性资本的表现形式，即资本有机构成。《资本论》中用第j部类产品当中消耗的不变资本对于可变资本的固定不变倍数hj表示该部类的资本有机构成。剩余价值Mj(t)与可变资本Vj(t)之间保持固定不变的比率，以ej表示，是第j部类的剩余价值率。以Yj(t)，Xj(t)分别表示第j部类新创造价值、总产值，那么按照经典的马克思再生产公式，在每个部类内部，不变资本、可变资本、剩余产品、新创造价值（产品）、总产值（产品）之间的关系被如式（1）所示的定义方程所确定：

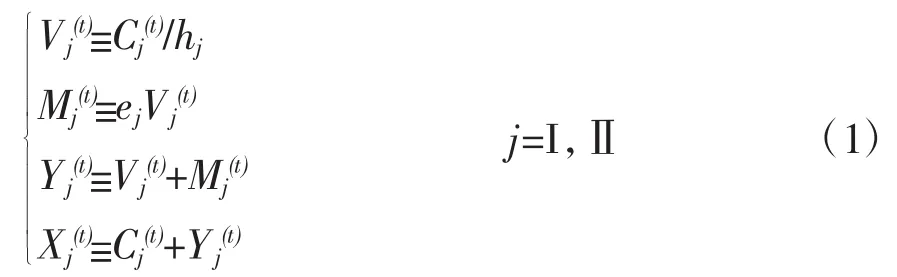
剩余价值Mj(t)是形成本部类的新增资本和企业所有者的剩余价值消费的唯一来源。对确定了含义的字母前面加符号△以表示增量，并用Mx(t)j表示第j部类企业所有者将本部类的剩余价值中用于个人消费的部分。因而剩余价值的使用确定了如式（2）所示的行为方程：

△Cj(t)+△Vj(t)+Mx(t)j=Mj(t)j=I，Ⅱ（2）

由于按照经典的马克思再生产公式和式（1），在每个部类内部，总产值的各构成部分之间保持固定不变关系，因而总产值增量的各构成增量之间也保持同样的固定不变关系。那么基于式（1），又存在如式（3）所示的行为方程。

实现再生产意味着当年的全部生产资料、消费资料的使用量与生产量平衡，因而分别有生产资料、消费资料的均衡条件：

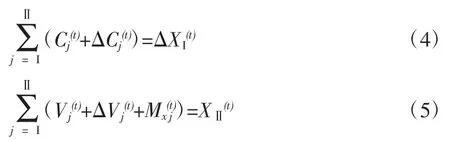
均衡条件式（4）和（5）在政治经济学教科书中被称为社会再生产的实现条件（程恩富等，2012）。[2]

式（1）、（2）、（3）、（4）、（5）合在一起，就是完整的再生产公式。其中，均衡条件式（4）、（5）是再生产公式的主要部分，而定义方程（1）和行为方程（2）、（3）则共同决定了马克思再生产公式所具有的特殊结构。如果在式（2）左、右两边都加上Cj(t)和Vj(t)，再将所得的两式相加，结果便与将式（4）、（5）相加得到的结果完全一样，都是全部社会总产品的需求等于供给。这说明，由于行为方程（2）的存在，式（4）、（5）两者中只有一个是独立的。现在将式（3）代入（2），得到：将式（3）、（6）都代入式（5）并化简，与直接将式（4）化简得到的结果完全一样：

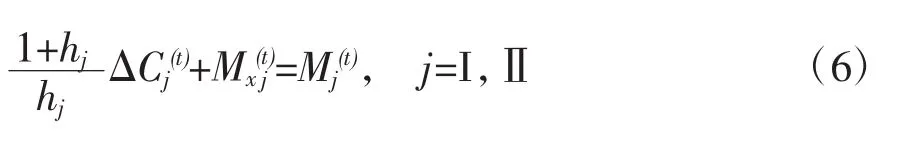
因此，式（7）就是简化的社会再生产线性方程组，是社会再生产的两个部类资本积累均衡方程。方程中有△CI(t)，△CⅡ(t)两个变量，是社会再生产的决策变量；方程中的（YI(t)-CⅡ(t)）在当时是既定的，但在不同的年代应是不同的，是社会再生产中的状态变量。在确定决策变量△CI(t)，△CⅡ(t)时，是把状态变量的值作为已经取定的，所以可以把状态变量看作是参数。实现社会再生产就是从这个资本积累均衡方程中确定一组△CI(t)，△CⅡ(t)的解，再代入式（3）和（6）得到△Vj(t)和Mx(t)j，就确定了扩大再生产的一种具体安排。由于企业所有者把本部类的剩余价值中用于个人消费的部分Mx(t)j≥0，所以根据式（6）可以确定对于决策变量的约束条件：

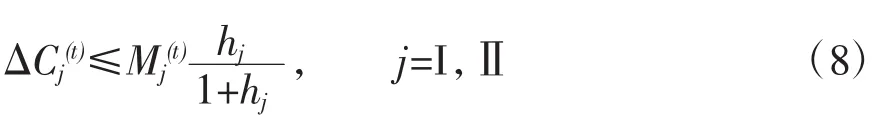
扩大再生产是指在至少每个部类的资本都不减少的前提下，社会总资本扩大。根据式（1）表明的每个部类的不变资本与总资本的固定关系，扩大再生产是在至少每个部类的不变资本都不减少的前提下，社会总不变资本扩大，也就是△CI(t)，△CⅡ(t)至少有一个大于零。于是对于扩大再生产的情形，对于决策变量还有约束条件：

将式（8）取j=Ⅰ，Ⅱ相加得到：

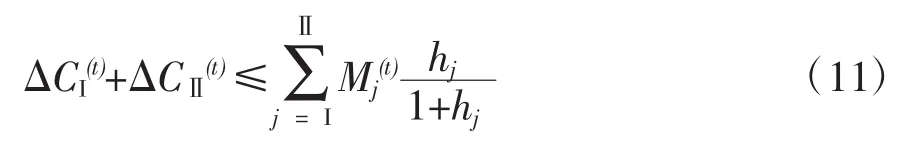
将式（10）和（11）代入资本积累均衡方程式（7），得到：

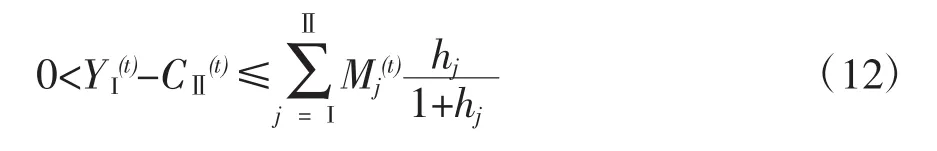
二、马克思扩大再生产公式的图解法

扩大再生产的两个部类资本积累均衡方程式（7）中有两个决策变量，根据这个方程以及对于决策变量的约束条件式（8）、（9）、（10），可以建立二维直角坐标系，运用图解法直观、简便地获得扩大再生产公式的解。

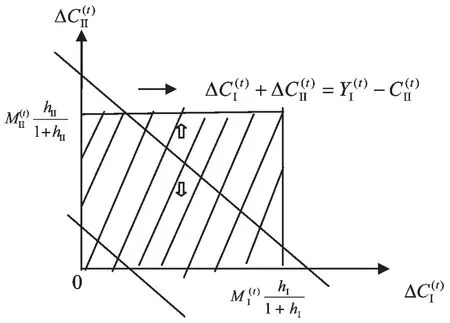
图1　马克思扩大再生产公式的图解法

如图1所示，分别以决策变量△CI(t)，△CⅡ(t)作为横、纵坐标建立直角坐标系，就可以运用平面解析几何方法获得扩大再生产公式的解。首先，对于决策变量的约束条件式（8）、（9）表明，△CI(t)，△CⅡ(t)的取值范围局限在由两条直线△CI(t)=MIhI/（1+hI）和△CⅡ(t)=MⅡhⅡ/（1+hⅡ）与两个坐标轴围成的矩形区域内；式（10）表明还要剔除坐标系的原点。资本积累均衡方程式（7）表示了一条直线，扩大再生产公式的解，都是这条直线上的点。结合决策变量△CI(t)，△CⅡ(t)的取值范围，△CI(t)，△CⅡ(t)取值的可行域是此直线处于矩形区域内的这部分线段。这条线段的斜率是-1，小于零，所以可行域线段呈左高右低状。对于社会再生产中的状态变量（YI(t)-CⅡ(t)）取不同值的情形，可以看作是这条线段随着参数取不同的值，可以在矩形区域内上、下平行移动；（YI(t)-CⅡ(t)）取值越大上移的位置就越高。不等式（12）表明，上述矩形区域的右上顶点，是方程式（7）表示的直线在△CI(t)，△CⅡ(t)的取值范围内能够上移到的最高位置。右上顶点的横、纵坐标分别是△CI(t)=MI(t)hI/（1+hI）和△CⅡ(t)=MI(t)hⅡ/（1+ hⅡ），代入方程式（7），就表示右上顶点在这条直线上，也就是直线上移到了最高位置。资本积累均衡方程式（7）表示的这条直线处于矩形区域内的这部分线段上的点，都是扩大再生产公式的解，所以先确定任何一点的横（纵）坐标就可以对应地确定纵（横）坐标；也就是一旦确定了资本积累均衡时的第Ⅰ（第Ⅱ）部类积累，就可以对应地确定第Ⅱ（第Ⅰ）部类积累。

首先考察先确定线段上的某一点的横坐标△CI(t)。那么该点的纵坐标是：

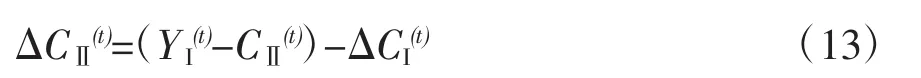
这代表着把第Ⅰ部类不变资本积累△CI(t)作为扩大再生产决策的自由变量，而把第Ⅱ部类不变资本积累△CⅡ(t)作为因变量或称为自由变量的函数。由于此线段呈左高右低状，所以在线段的左端点横坐标数值最小，纵坐标数值最大；在右端点横坐标数值最大，纵坐标数值最小。根据图1所示的此线段上下平行移动时所处的两个不同位置，可以看出左端点横坐标数值是：

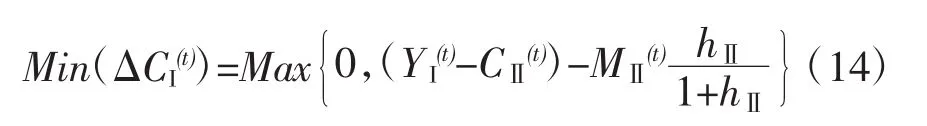
所以，当把第Ⅰ部类不变资本积累△CI(t)作为扩大再生产决策的自由变量，它的定义域是：

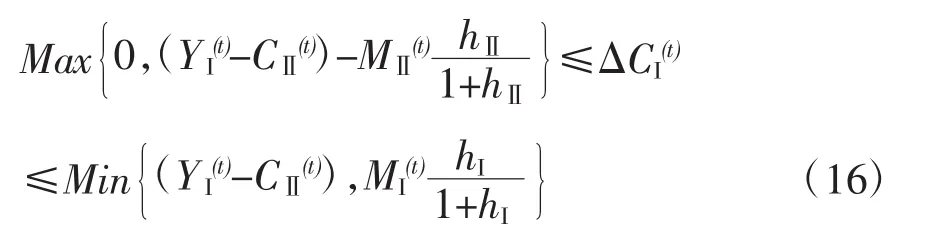
右端点横坐标数值是：

将△CI(t)在此定义域内任意取一个数值，再代入式（13）得到相应的△CⅡ(t)数值，就获得扩大再生产公式的一个解。式（13）与（16）构成的扩大再生产公式的图解法，与已经有研究给出的求解扩大再生产问题的代数方法完全一致（陶为群，2014）。[1]

再考察先确定线段上的某一点的纵坐标△CⅡ(t)。那么该点的横坐标是：

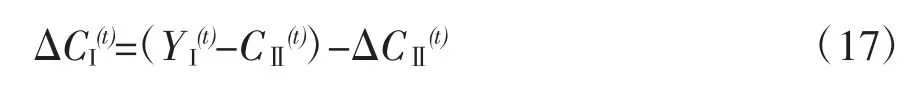
这代表着把第Ⅱ部类不变资本积累△CⅡ(t)作为扩大再生产决策的自由变量，而把第Ⅰ部类不变资本积累△CI(t)作为因变量或称为自由变量的函数。由于此线段呈左高右低状，所以在线段的左端点纵坐标数值最大，横坐标数值最小；在右端点纵坐标数值最小，横坐标数值最大。根据图1所示的此线段上下平行移动时所处的两个不同位置，可以看出左端点纵坐标数值是：

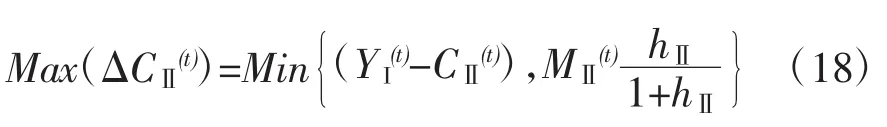
右端点纵坐标数值是：

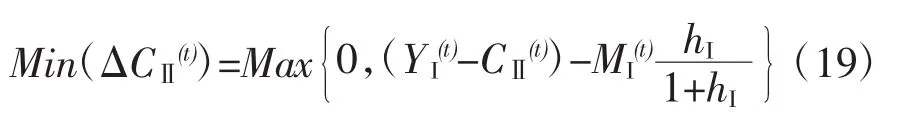
所以，当把第Ⅱ部类不变资本积累△CⅡ(t)作为扩大再生产决策的自由变量，它的定义域是：

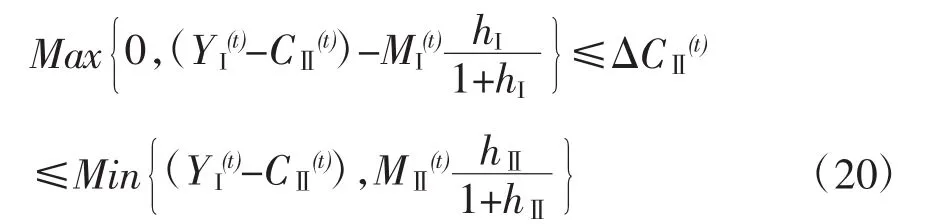
将△CⅡ(t)在此定义域内任意取一个数值，再代入式（17）得到相应的△CI(t)数值，就获得扩大再生产公式的一个解。式（17）与（20）构成的扩大再生产公式的图解法，也与已经有研究给出的求解扩大再生产问题的代数方法完全一致（陶为群，2014）。[1]

从马克思扩大再生产公式的图解法看到，式（12）表明的扩大再生产中的状态变量（YI(t)-CⅡ(t)）的取值区间，是扩大再生产公式有解的充分必要条件。根据式（1），每个部类内部各个部分之间的相互比例是固定的，所以两个部类产品之间任一个对应部分之间的比例关系，都足以表现整个部类之间的比例关系。现在，用两大部类新创造价值之间的比例关系从总体上反映两大部类之间的比例关系，记为φ(t)=YⅡ(t)/YI(t)。将（1）式和φ(t)所表示的关系代入扩大再生产公式有解的充分必要条件式（12），得到两大部类比例φ(t)取值的一个限制区间。

φmin≤φ(t)＜φmax，式中

按照马克思社会再生产理论，充分必要条件式（12）中的状态变量（YI(t)-CⅡ(t)）在实物形态上是生产资料，而社会总产品是由生产资料、消费资料两种不同用途的实物产品共同组成，因而式（12）表明了对生产资料的相对最低、最高数量要求。而式（21）是把对生产资料的相对最低、最高数量要求，转换成对于两大部类产品比例φ(t)取值范围的限制。

三、扩大再生产公式的图解法的验证

下面引用马克思《资本论》第二卷第二十一章中所举的第一例，对扩大再生产公式的图解法加以计算验证。[3]此例设定两个部类结构参数hI=4倍，hⅡ=2倍，eI=eⅡ=100%，来说明一般情形下两大部类的扩大再生产过程。直接引用该例中的第1年（起始年）的两大部类生产和资本积累数据，列在表1。根据此例第1年的数据，状态变量（YI(t)-CⅡ(t)）取值500，满足约束条件式（12）。此例是先决定第Ⅰ部类的剩余价值积累率为50%，也就是把第Ⅰ部类不变资本积累△CI(t)作为扩大再生产决策的自由变量，△CI(t)取值400处于式（16）确定的定义域内。此例确定的第Ⅱ部类不变资本积累△CⅡ(t)取值100满足式（13），这样确定的扩大再生产的解，就是图1坐标系当中的点（400，100），此点在线段△CI(t)+△CⅡ(t)= 500上。因此，此例验证了扩大再生产公式的图解法。

表1　引用《资本论》第二卷第二十一章中第一例验证图解法

［参考文献］

［1］陶为群.两大部类扩大再生产的充分必要条件与求解［J］.经济数学，2014，（3）.

［2］程恩富，冯金华，马艳.现代政治经济学新编（完整版·第二版）［M］.上海：上海财经大学出版社，2012：204-210.

［3］［德］马克思.资本论：第2卷［M］.北京：人民出版社，2004：574-585.

［责任编辑：杨彧］

［中图分类号］F091.91

［文献标识码］A

［文章编号］1673-8616（2015）01-0038-04

［收稿日期］2014-09-16

［作者简介］陶为群，中国人民银行南京分行副行长、研究员、安徽财经大学兼职教授（江苏南京，210004）。