涉及Fibonacci数列与Chebyshev多项式的一些反正切
张潇潇,胡 宏
(1.宁夏大学 数学与计算机学院,宁夏 银川 750021; 2.淮阴师范学院 数学科学学院,江苏 淮安 223300)
涉及Fibonacci数列与Chebyshev多项式的一些反正切
张潇潇1,2,胡 宏2
(1.宁夏大学 数学与计算机学院,宁夏 银川 750021; 2.淮阴师范学院 数学科学学院,江苏 淮安 223300)
根据Fibonacci数列和两类Chebyshev多项式的基本性质,利用反正切函数得出了一些关于黄金分割数与Fibonacci数列及Lucas数列的恒等式,同时获得了一些涉及两类Chebyshev多项式之间关系的恒等式.
黄金分割数; Fibonacci数列; Lucas数列; Chebyshev多项式; 反正切函数
0 引言
著名的Fibonacci数列{Fn}和Lucas数列{Ln}满足如下递推关系[1]:
Fn+2=Fn+1+Fn,F0=0,F1=1,n=0,1,2,…
Ln+2=Ln+1+Ln,L0=2,L1=1,n=0,1,2,…
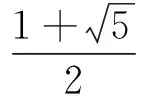
同样地,第一类Chebyshev多项式Tn(x)和第二类Chebyshev多项式Un(x)满足如下递推关系[2]:
Tn+2(x)=2xTn+1(x)+Tn(x),T0(x)=1,T1(x)=x,n=0,1,2,…,
Un+2(x)=2xUn+1(x)+Un(x),U0(x)=1,U1(x)=2x,n=0,1,2,…

1 涉及φ,Fn,Ln的反正切
引理1[4]设x,y为实数,有
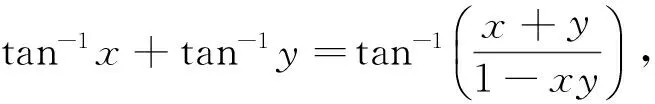
(1)
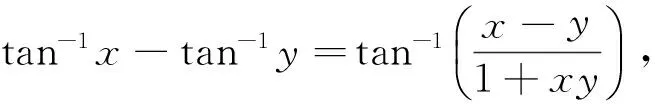
(2)
定理1 设m,k,r为任意整数,当mk±r≠0时有
(3)
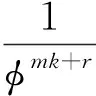
(4)
同样地,由式(2)可得
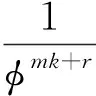
(5)
又因为φ>0,所以φmk+r>0,φmk-r>0,从而
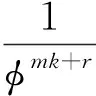
(6)
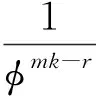
(7)
式(4),式(5)两式相加,再将式(6)带入,可得式(3)成立.
注Kunle Adegoke在文[4]中定理2.2就是在定理1中取m=2,r=1及m=2,r=-1时的特殊情况;文[4]中定理3.1就是在定理1中取m=2,r=0时的特殊情况;文[4]中定理3.2就是在定理1中取m=r=2时的特殊情况.
引理2 设m,k,r为任意整数,则
(8)
(9)

当m是偶数时,
又由式(5)可知
从而
又由式(5)可知
从而
故式(6)和式(7)成立.
定理2 设n为任意整数,m是奇数,则
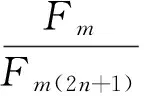
(10)
证明由式(9)可得
将以上两式相减可得证式(10)成立.
离休老干部由于多种因素对其心理状态有一定的影响,临床治疗中护理工作的积极有效的开展具有重要的作用。人文关怀可以对其进行心理需求的慰藉,给予充分的关心关怀,有效的改善其心理不良状态,积极配合临床治疗护理工作的开展,对其身体的康复具有促进作用。本文主要应用人文关怀在离休老干部心理护理中效果分析,研究离休老干部病房收治的84例,将相关资料整理并进行如下的阐述。
2 涉及Tn(x),Un(x)的反正切
定理3 设n为任意整数,∀x:x>1,则

(11)
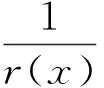
(12)
证明当x>1时,易知
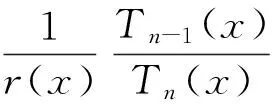
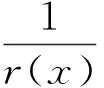
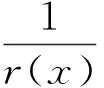
推论1 设n为任意整数,∀x:x>1

(13)

推论2 设为n任意整数,则

(14)
在定理3中令x=2,可得
推论3 设为n任意整数,则
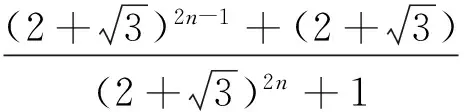
(15)

推论4 设n为任意整数,则
(16)
引理3 设k为任意整数,∀x:|x|>1,则
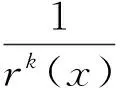
(17)
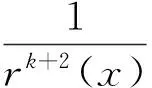
(18)
证明当∀x:|x|>1时,有
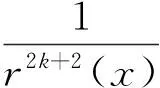
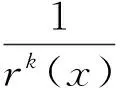
(19)
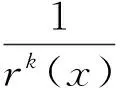
(20)
式(19)和式(20)两式相加得式(17),把式(19)和式(20)两式相减得式(18).在式(17)中令k=n,式(18)中令k=n-2,两式相减可得
定理4 设n为任意整数,∀x:|x|>1,则
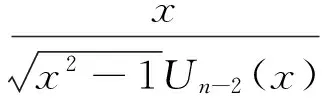
(21)
由式(1)可得
定理5 设n为任意整数,∀x:|x|>1
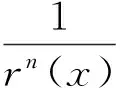
(22)
定理6 设n为任意整数,∀x:|x|>1

(23)
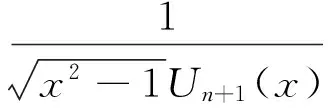
(24)
证明在式(17)中令k=n结合定理5可得式(23);在定理5中令k=n+2,结合在式(18)中令k=n可得式(24).
定理7 设n为任意整数,∀x:|x|>1则
(25)
证明由式(20)知
又因为
从而
即
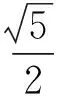
推论5 设n为任意整数,则
(26)
[1]Zhao F Z,Wang T M.Some identities involving the Fibonacci and Lucas numbers[J].Ars Combinatoria,2004,72:311-318.
[2]张文鹏.关于费波那奇数与契贝谢夫多项式[J].咸阳师范专科学院学报,1992,14(6):1-2.
[3]杨存典.关于第二类契贝谢夫多项式的一些恒等式[J].商洛师范专科学报,2002,16(4):6-8.
[4]Kunle A.The golden ratio Fibonacci numbers and BBP-type formulas[J].The Fibonacci Quarterly,2014,52(2):129-138.
[5]Chan H C.In terms ofφ[J].The Fibonacci Quarterly,2006,44(2):141-144.
[6]Hoggatt V E,Ruggles I D.A primer for the Fibonacci numbers:part V[J].The Fibonacci Quarterly,1964,2(1):46-51.
[7]Zhang W P.Some identities involving the Fibonacci numbers[J].The Fibonacci Quarterly,1997,35(3):225-229.
[8]Yuan Y,Zhang W P.Some Identities Involving the Fibonacci Polynomials[J].The Fibonacci Quarterly,2002,40(4):314-348.
[责任编辑:李春红]
SomeIdentitiesInvolvingArctangentofFibonacci
SequencesandChebyshevPolynomials
ZHANG Xiao-xiao1,2,HU Hong2
(1.School of Mathematics and Computer Science,Ningxia University,Yinchuan Ningxia 750021,China)
(2.School of Mathematical Science,Huaiyin Normal University,Huaian Jiangsu 223300,China)
In this paper,we derive some interesting identities involving golden ratio,Fibonacci sequences,Lucas sequences and the first and second type of Chebyshev polynomials by using the arctangent function.
golden ratio; Fibonacci; lucas; chebyshev polynomials; arctangent
2015-03-23
胡宏(1967-),女,江苏金湖人,教授,研究方向为数论与组合数学. E-mail:hysyhh@163.com
0157
:A
:1671-6876(2015)03-0197-06

