基于多元函数约束条件的变分极值在最优控制中的应用
吴群妹
(无锡科技职业学院 理科教学部,江苏 无锡 214000)
基于多元函数约束条件的变分极值在最优控制中的应用
吴群妹
(无锡科技职业学院 理科教学部,江苏 无锡 214000)
根据整型多元函数约束条件的变分极值定理,给出系统在给定性能指标达到最优时的最优控制以及最优轨线的必要条件,并且用实例加以验证.
条件极值; 泛函变分; 最优控制
0 引言
最优控制作为现代控制理论的重要组成部分,所要解决的主要问题是如何在给定条件下,确定一种合理的控制规律,使被控对象在预先规定意义上的性能指标具有最优值[1].该类问题也已经有很多人研究,如梁秀娟[2],唐旭清[3]人等.但是他们没有具体的给出在整型多元函数约束条件下系统达到最优控制和最优轨线的必要条件.本文根据整型多元函数约束条件的变分问题,给出系统在给定性能指标达到最优值时的最优控制以及最优轨线曲线方程的必要条件,并且将其应用于最优控制问题中.
1 整型约束条件变分问题

设泛函

(1)
整型约束条件
φi(t,x1,x2,…,xn)=0(i=1,2,…,m;m (2) 边界条件 (3) 研究J在约束条件以及边界条件下的极值问题,下面给出相关定理. 定理2 在整型约束条件(2)以及边界条件(3)下,目标泛函(1)取得极值的必要条件为 (4) 其中λi(t)为待定系数(i=1,2,…,m;m 证引入待定函数λi(t),作辅助函数 (5) 则辅助泛函 (6) 由定理1,式(1)的变分为 (7) 用λi(t)乘式(2)并在区间[x0,x1]上积分,得 (8) 对上式变分得 (9) (10) 因为λi(t)(i=1,2,…,m)是m个任意待定的函数,故可假定它由下面m个线性方程来决定. (11) 这里假定φi(i=1,2,…,m)是相互独立的,即至少要有一个m阶函数行列式不为零, (12) 就可以由式(11)求得λi(t)(i=1,2,…,m)的解.这时式(10)中剩下的变分项只有δx(m+1),δx(m+2),…,δxn,共n-m项, (13) 这里n-m项都是相互独立的,根据定理1将式(11)和式(13)合并就得到了式(14) (14) 证毕. 在控制理论中,所求的泛函极值曲线往往有一定的约束条件,常见的约束条件是状态方程[6].状态方程一般形式可以写成 (15) 式中x为n维向量,u为m维向量函数,m (16) 在约束条件(15)下取极值.引入待定函数λ(t),作辅助函数H(x,u,λ,t), H(x,u,λ,t)=F(x,u,t)+λ(t)f(x,u,t). H(x,u,λ,t)=F+λ(t)f(x,u,t) (17) 由定理2,在约束条件(15)下,辅助泛函 (18) 对(18)式第二项分部积分 (19) 代回(18)式得 (20) 设u(t)和x(t)相对于最优控制u*(t)及最优轨线x*(t)的变分为δu(t)和δx(t),则J*的变分为 (21) 使J*取得极值的必要条件是δJ*=0,即 (22) (23) 因此对于系统(15)与性能指标(16),如果初始时刻与初始状态、终止时刻与终止状态都固定,则u*(t)与x*(t)是最优控制和最优状态轨线的必要条件是:存在一协态向量λ(t),使λ(t)、u*(t)以及x*(t)满足 (24) 边界条件满足x(t0)=x0,x(T)=xT. 例1 给定系统的状态方程 在求多元函数系统约束性能指标极值的最优控制和最优状态轨线时,应用整型约束的变分极值定理是一个非常好的办法.本文仅对简单的系统的最优控制进行讨论,后面还可以针对其他复杂系统最优控制作进一步讨论. [1]张莲,胡晓倩,王彬,等. 现代控制理论[M]. 北京:清华大学出版社,2008. [2]梁秀娟,嵇海旭. 用变分法实现现代控制系统中的最优控制[J]. 装备制造技术,2013(2),73-74. [3]唐旭清,翁昊年. 变分法在最优控制问题中的一个应用[J]. 江南大学:自然科学版,2003,2(5),521-524. [4]老大中. 变分法基础[M]. 北京:国防工业出版社,2008:185-218. [5]贾小勇. 欧拉变分法基本方程不变性思想及其探源[J]. 西北大学学报:自然科学版,2011,41(3),537-542. [6]朱肖伟. 最优控制理论与应用中的若干问题[M]. 北京:科学出版社,2007. [责任编辑:李春红] TheApplicationinOptimalControlbasedonVariationalExtremumofMultiFunctionConstraints WU Qun-mei (Wuxi Technology and Professional College,Wuxi Jiangsu 214000,China) According to an integer multivariate function constraint variational minimum theorem,a necessary condition for optimal control and optimal trajectories are given when the performance achieved optimal and be verified with a example. conditional extreme value; functional variation; optimal control 2015-05-24 吴群妹(1981-),女,江苏苏州人,讲师,硕士,研究方向为应用数学、最优控制等. E-mail:wuqunmeixiangxiang@163.com O177.92; O232 :A :1671-6876(2015)03-0193-04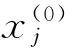

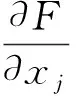

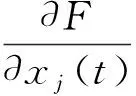
2 变分问题在最优控制中的应用





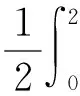
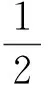
3 小结

