第二类r-置换因子循环矩阵的性质及谱分解

(1.西安培华学院基础部，陕西 西安 710125；2.文山学院数学学院，云南 文山 663000)

·基础学科·

第二类r-置换因子循环矩阵的性质及谱分解

胡 艳1，陆亚哲2

(1.西安培华学院基础部，陕西 西安 710125；2.文山学院数学学院，云南 文山 663000)

给出第二类r-置换因子循环矩阵的概念及一些基本性质。利用第二类r-置换因子循环矩阵的特征值和非奇异矩阵的充要条件，得出第二类r-置换因子循环矩阵的谱分解。

第二类r-置换因子循环矩阵；非奇异；谱分解

循环矩阵、r-循环矩阵、r-置换因子循环矩阵都是有趣的特殊矩阵，这些特殊的矩阵在编码理论、系统辨识、信号处理、计算机时序分析等诸多方面都有广泛的应用，关于这些循环矩阵的概念和性质在文献[1-4]中都有涉及。文献[4]研究了r-循环矩阵的特征值问题，文献[5-10]研究了第二类r-循环矩阵的性质及对角化、块置换因子循环矩阵的问题；但目前关于本文给出的第二类r-置换因子循环矩阵的相关研究却未见报道。

1 基本概念

定义1[1]称一个n阶置换矩阵P为基本置换因子循环矩阵当且仅当Pn=En，这里n是满足该式的最小正整数。

定义2 设P为满足定义1的n阶基本置换因子循环矩阵，对于Mn中的矩阵πr如果满足

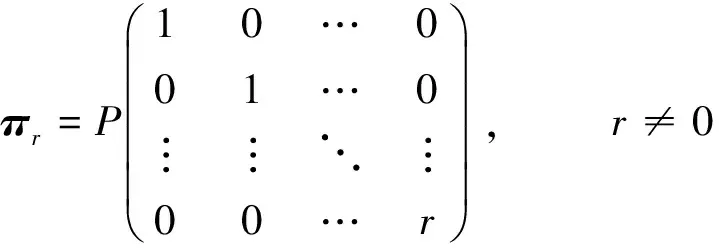
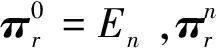
定义3 设πr∈PrCMn,对于Mn中的矩阵A,存在多项式

f(x)=a0+an-1x+an-2x2+…+a1xn-1，

称f(x)为A的伴随多项式。

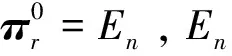
定义4[2]若n阶矩阵P∈Cn×n满足条件P2=P,则称P为幂等矩阵。

引理1[7]AT与A有相同的特征值。

引理2[7]vandermonde矩阵

的逆矩阵存在，且

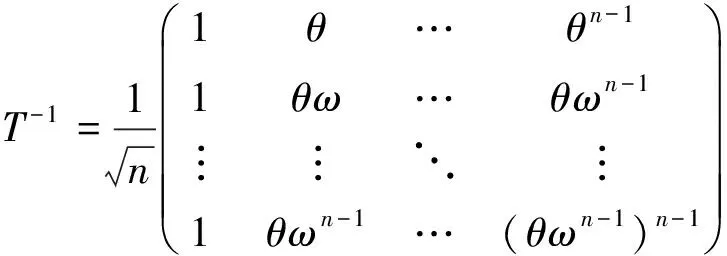
其中ω是n次本原单位根，θωj(0≤j≤n-1)是xn-r=0的n个不同的根。

2 主要结果

2.1基本性质

性质1 若πr为满足定义2中的n阶第二类r-置换因子循环矩阵，对于Mn中的矩阵A,若A∈PrCMn,则πrA=Aπr。

证明因为A∈PrCMn,由定义可得

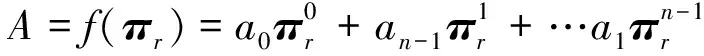
则

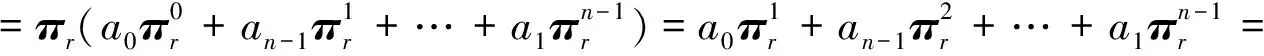
性质2 设矩阵K1,K2∈PrCMn,则K1+K2=K2+K1∈PrCMn,K1K2=K2K1∈PrCMn。

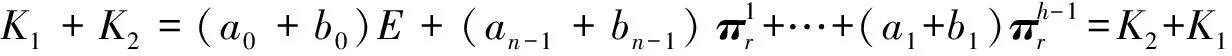
故K1+K2仍是πr的多项式，即K1+K2∈PrCMn。

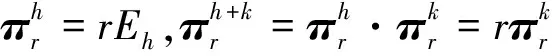
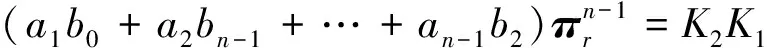
则K1K2仍是πr的多项式，因而K1K2∈PrCMn。

性质3A∈PrCMn可逆，则A-1∈PrCMn。

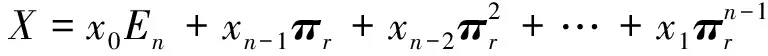
构造方程组

(1)

因为矩阵A可逆，所以方程组(1)有唯一解x0,xn-1,xn-2,…x1。且由方程组(1)可得

(2)

由式(2)可得

因此X为矩阵A的逆矩阵A-1,且A-1也是第二类r-置换因子循环矩阵。

2.2谱分解

定理1 设A∈PrCMn则A的特征值λj=f(θωj)=a0+an-1(θω)+…+a1(θωn-1)n-1,a0,a1,…,an-1是A的第一行元素(ai0,ai1,…,ain-1)对于置换矩阵πr的一个重排，其中ω是n次本原单位根，θωj(0≤j≤n-1)是xn-r=0的n个不同的根,f(x)=a0+an-1x+…+a1xn-1。

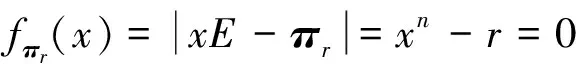
由特征值xi可求出相应的特征向量

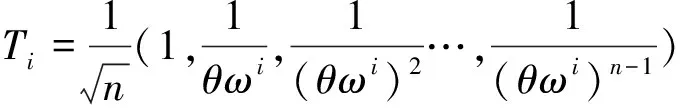
令T=(T0,T1,…Tn-1)，即

所以T-1πrT=diag(x0,x1,…,xn-1)=diag(θ,θω,…，θωn-1)；

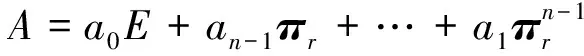
所以A的特征值是λi=f(θωi)。

推论1 若A∈PrCMn,且A=Percirpr(a0,a1,…，an-1),则A非奇异的充要条件是f(θωi)≠0(i=0,1,2,…,n-1)。其中第一行元素为(a0,a1,…,an-1)的第二类置换因子循环矩阵A记为A=Percircr(a0,a1,…,an-1)。

此推论易证。

定理2 设A∈PrCMn,并且有n个互异特征值f(λ0),f(λ1),…,f(λn-1),则A可对角化的充分必要条件是，存在n个幂等矩阵P0,P1,…Pn-1满足:

2)PiPj=0,当i≠j时；

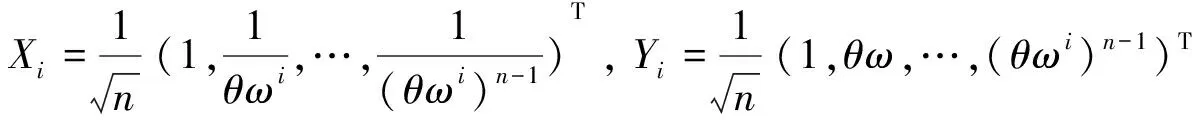
可以得到

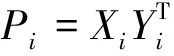
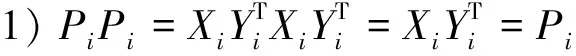
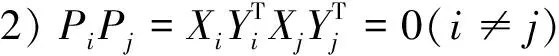
因而Pi是幂等矩阵。

令X=(X0,X1,…,Xn-1),Y=(Y0,Y1,…,Yn-1)。

通过验证可得：Y是X的逆矩阵，所以

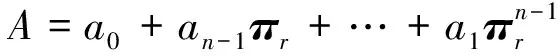
可得

故A与对角矩阵相似，因而A可对角化。

必要性：由πr的特征多项式xn-r,可得πr有n个互不相同的特征值λ0,λ1,…λn-1,从而可以得出对应的特征向量分别为

由定理1可知，A的特征值为f(λo),f(λ1),…,f(λn-1)。

由引理3可知，AT的特征值也为f(λo),f(λ1),…,f(λn-1)。

同理可得AT的特征值所对应的特征向量为

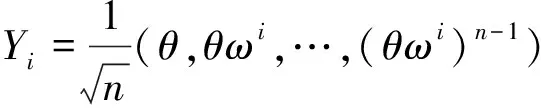
令

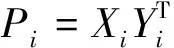
很容易验证：Pi满足1)、2)、3)

由

从而可得到

由引理4可得

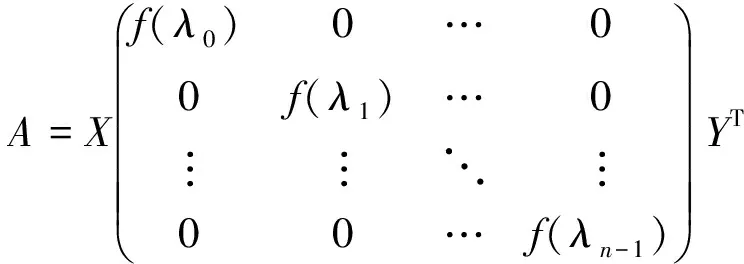
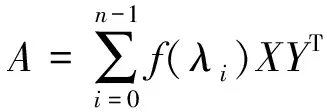
通过定理2,可得出求第二类r-置换因子循环矩阵的谱分解的一般步骤：

1)由置换因子循环矩阵A∈PrCMn,找出πr,得到特征多项式f(x)；

2)求出特征值，进而求出A特征向量以及左特征向量；

3)得到Pi，进而求出A的谱分解。

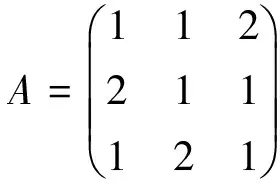
解：由

可得A是第二类r-置换因子循环矩阵，且r=1。

所以

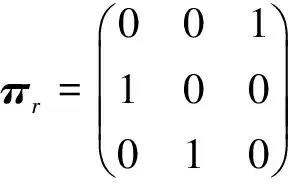
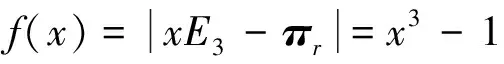
进而求出特征向量分别为：

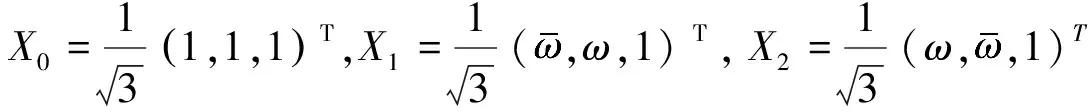
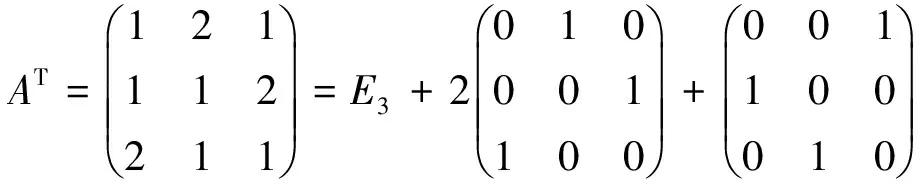
同理可以求得AT的特征向量分别为：

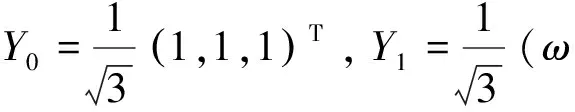
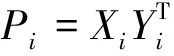
即

所以

[1]高殿伟.广义循环矩阵[J] .辽宁师范大学学报：自然科学版,1988(2):7-11.

[2]江兆林,刘三阳,张圣贵.求置换因子循环矩阵的逆阵及广义逆阵的快速算法[J] .高等学校计算数学学报, 2003, 25(3): 227- 234.

[3] Davisp.Matrices[M],Newyork:John Wiley,1979.

[4]王金林,戴华.r-循环矩阵特征值反问题[J].科技通报,2005, 5(9):505-509.

[5]赵立宽,李振,孟令霞.关于第二类r-循环矩阵的几个性质[J].曲阜师范大学学报：自然科学版,2009, 35(4): 34-36.

[6]兰远姣，何承源.第二类r-循环矩阵的判定条件及其对角化[J].曲阜师范大学学报：自然科学版,2011, 37(1):24-28.

[7]吴昌悫 ,魏洪增.矩阵理论与方法[M].北京：电子工业出版社,2006.

[8]胡艳,秦克云,孙继忠.r-块置换因子循环矩阵及其逆矩阵的求法[J].重庆师范大学学报：自然科学版,2012,29(4):63-67.

[9]毛纲源.循环矩阵及其在分子振动中的应用[M].武汉：华中理工大学出版社,1995.

[10]Stuart J L, Weaver J R. Matrices that Commute with a Permutation Matrix[J]. Linear Algebra and Its Appl, 1991, 150: 255-265.

(编校：叶超)

CharactersandSpectralDecompositionOftheSecondKindofr-permutationfactorCirculantMatrix

HU Yan1, LU Ya-zhe2

(1．DepartmentsBasicCourses，Xi’anPeihuaUniversity,Xi’an710125China；2.CollegeofMaths,WenshanUniversity,Wenshan610031China)

The concept and some characters of the second kind of r-permutation factor circulant matrix are given. Based on the Eigenvalues and the necessary and sufficicent condition of nonsingularity of the second kind of r-permutation factor circulant matrix, sepectral decomposition of the second kind of r-permutation factor circulant matrix is obtained.

the second kind of r-permutation factor circulant matrix ; nonsingularity; spectral decomposition

2014-10-07

国家自然科学基金(61473239);文山学院科研基金项目(14WSY01)

胡艳(1984—)，女，助教，主要研究方向为智能信息处理。

O151

：A

：1673-159X(2015)03-0083-06

10.3969/j.issn.1673-159X.2015.03.017