基于决策类划分的新型多变量决策树算法

(泉州经贸职业技术学院信息系，福建 泉州 362000)

·计算机软件理论、技术与应用·

基于决策类划分的新型多变量决策树算法

黄俊南

(泉州经贸职业技术学院信息系，福建 泉州 362000)

基于不可分辨关系、复合运算、集合运算和逻辑运算等集合论概念，构造一种新型的多变量决策树算法。该算法包括5个步骤：依据决策属性值划分出决策类；利用决策类之间条件属性集相交判断二义性条件属性值；利用决策类各条件属性值域的不同判断独立决策条件属性值；利用决策类自身条件属性集进行复合运算，获得多变量决策方法；使用或运算符(∨)连接各个部分的决策规则以取得完整的决策规则。以决策树典型训练集(气象信息系统)为例进行验证，其结果表明，该算法行之有效。通过时间复杂度的分析结果表明，该算法较之粗糙集算法更优，而且不亚于ID3算法。

单变量决策树；多变量决策树；决策表；集合运算；逻辑运算

决策树是用于模拟人们对于某种决策而进行的一系列判断过程的树形图。其分类方式近年来被广泛作为商业领域、科学研究等相关决策问题的解决方案。

决策树的构造算法有很多种运算方式，典型代表是Quinlan提出来的ID3算法[1]。此后他又提出了ID3的优化算法即C4.5算法[2]。此类算法是基于单变量构造的决策树(只检验单个属性)，这一限制使得对很多复杂概念的表达变得困难或无法表达[3]；因此，人们提出了多变量归纳学习系统。粗糙集多变量算法是将粗糙集中的相对核作为初试测试属性集合，采用粗糙集中的知识代替ID3的信息熵作为选择扩展属性的度量，在一些情况下，它能获得比ID3算法更简洁的决策树[4]。其典型代表有苗夺谦等[3]提出的基于粗糙集的多变量决策树的构造方法、吴强等[5]提出的基于非线性拟合方程的多变量决策树算法等。本文采用一个新的视角进行多变量决策树的构造，其主要目的是降低决策树构造过程的数据运算量及其复杂度，并提出较为易懂的运算过程。

1 主流决策树算法建树及简化的逻辑规则

目前，主流的决策树算法的代表是单变量算法ID3和多变量粗糙集算法[6-16]。本文利用表1的数据集[1]作为训练集。

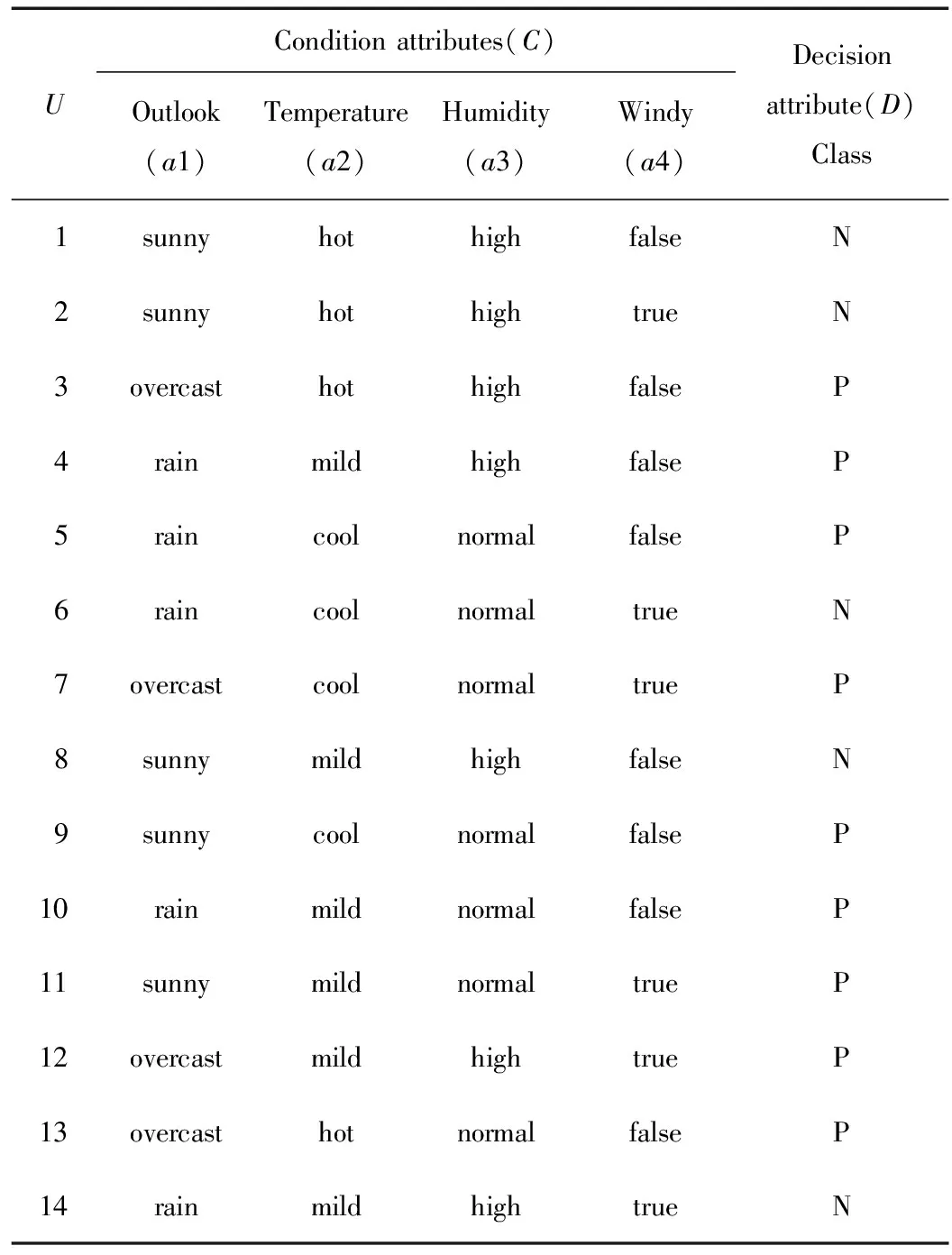
表1 一个关于气象信息系统表(训练集)

对表1数据分别根据ID3算法和粗糙集多变量粗糙集算法进行递归建树，得到的决策树如图1(a)和(b)所示。

对图1的2种构建过程使用“if-then”规则进行分类记录并简化，均可得如下逻辑规则：

If (outlook=”sunny” and humidity=”high”)or (outlook=”rain” and windy=”true”)

Then class=”N”; --class为N的逻辑规则

If (outlook=”sunny” and humidity=”normal”)or (outlook=”rain” and windy=”false”)or outlook=”overcast”

Then class=”P”;--class为Y的逻辑规则

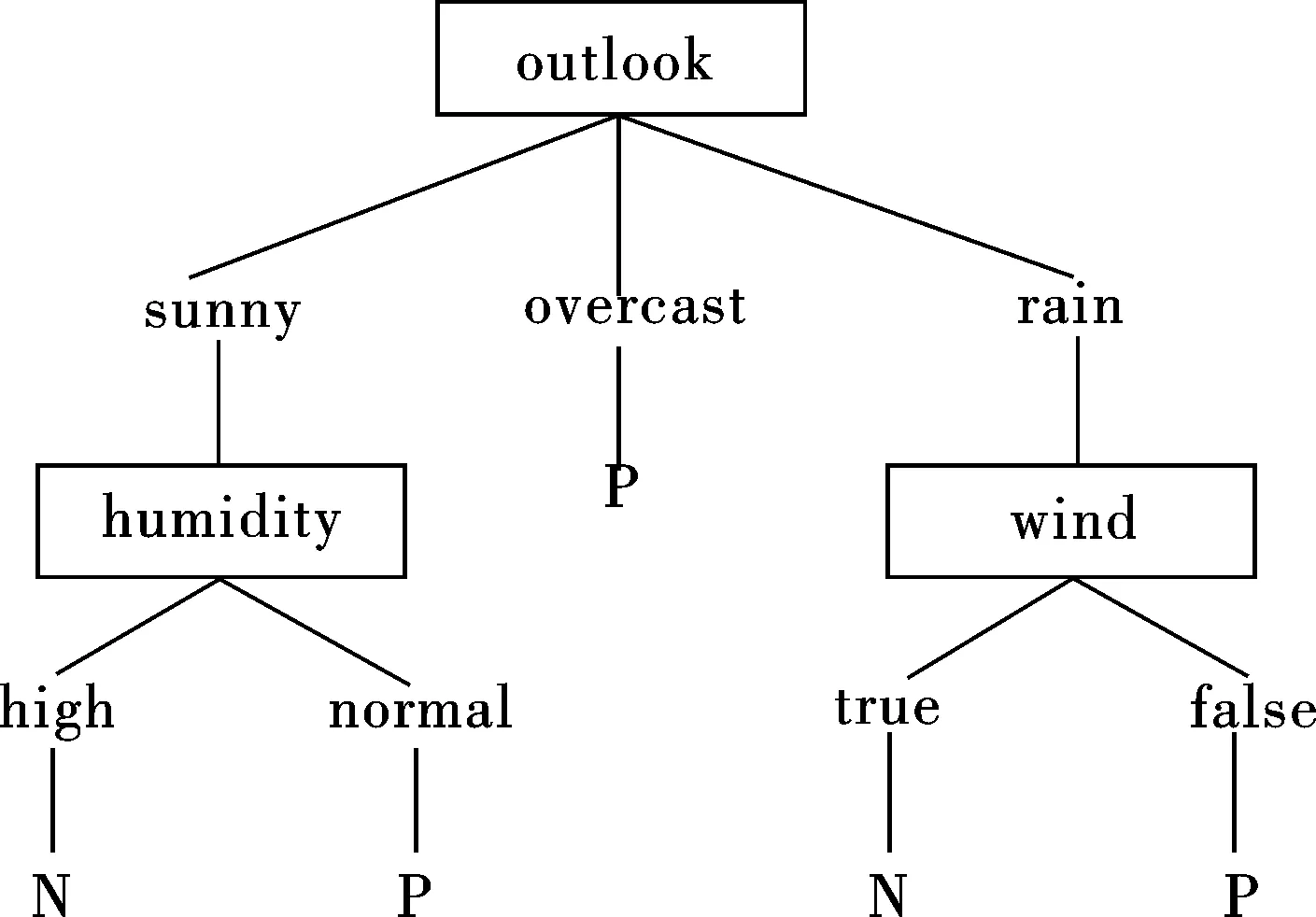
(a) ID3单变量决策树

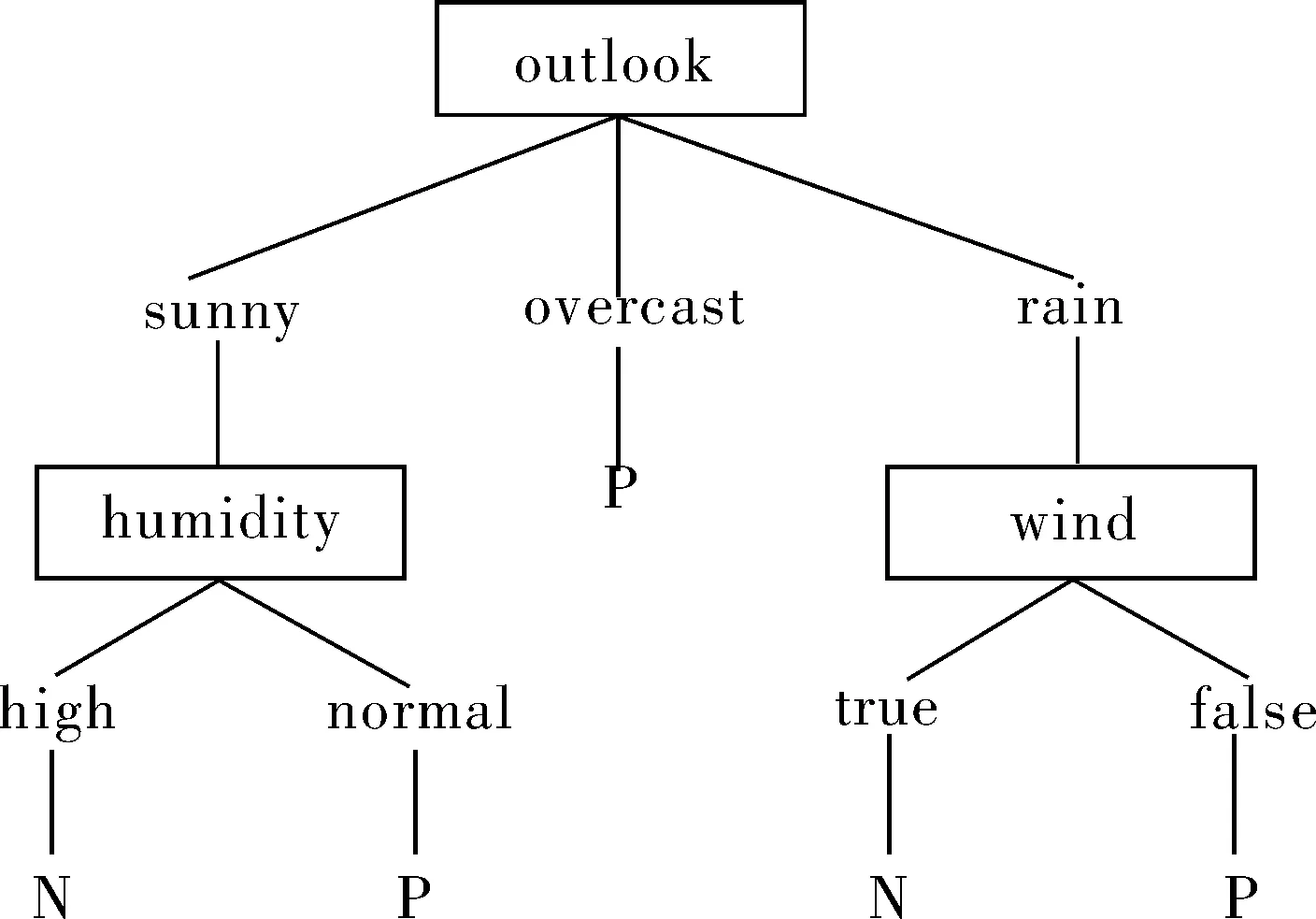
(b)粗糙集多变量决策树

2 决策类划分的多变量决策树算法构造过程

2.1决策表定义

一个决策表可以形式化定义[6]为：S=，其中U={u1,u2,…,un}是所感兴趣对象的有限集合，C∪D是属性的有限集，C为条件属性集，D为决策属性集，并且C∩D=∅，V为属性集C∪D的值域，f:U×(C∪D)→V为一个信息函数，表示任一对象的属性在V上的取值，即f(x,r)∈Vr，它指定了U中每个对象x的属性值。决策表S=中的依赖关系C→kD决定了一套if…then…形式的规则集。从逻辑观点出发，决策规则将形如a=v(a为属性名，v为属性值)的基本公式是利用连接词语“与” “或”和“蕴含”连接起来所建立的蕴含式。蕴含式前件表示条件，后件表示决策[7]。

2.2新型决策树算法描述

算法首先依据决策属性值划分出各自独立的决策类，利用决策类之间条件属性集相交判断并排除掉二义性，然后利用决策类各条件属性值域的不同判断并排除独立决策条件属性值，接着利用复合运算对自身条件属性集进行运算获得多变量决策规则，最后使用或运算符对运算后的单独决策规则和多变量决策规则进行连接以获取完整的决策规则。其相关算法描述如下：针对决策表形式化定义S=，其中C是条件属性集，D是决策属性集。假设C={c1,c2,…,cn}，c1～cn表示各条件属性。算法包含5个步骤。

步骤1:根据决策属性划分论域。使用不可分辨关系[7]对决策表U进行决策类划分，令集合Vd表示决策属性d的值域，设Vd={d(1),d(2),…,d(p)}表示决策值，值域个数为p，则决策属性d将论域U划分成{Ud(1),Ud(2),…,Ud(p)}。

步骤2:排除二义性[8]条件属性。如果一个文法存在某个句子对应2棵不同的语法树，则说明这个文法是二义的。二义性条件属性体现为相同的条件属性值能推导出不同的决策属性值，当决策类存在这种条件属性，决策分析将无法准确推导。对全部决策类分析并排除。

1)判断。假设存在2个决策类Ud(x1),Ud(x2)⊂U，其中1≤x1,x2≤p，且x1≠x2，这2个决策类的条件属性集分别是Cd(x1),Cd(x2)⊂C。设2个属性集相交后集合为Cd(x12)=Cd(x1)∩Cd(x2)，当Cd(x12)≠∅，则说明这2个决策类存在二义性条件属性值，使得Cd(x12)→Dd(x1)和Cd(x12)→Dd(x2)成立，且Dd(x1)≠Dd(x2)。

步骤3:分析并取得独立决策条件属性。当决策类中某些条件属性值不属于其他决策类时，则称此类属性值为独立决策条件属性值(简称独值)，可直接引作决策规则。

1)判断独值。重设Ud(j)为排除二义性条件属性值后的决策类。用ci(d(j))表示c1(d(j))～cn(d(j))条件属性，1≤i≤n。设决策类Ud(j)的条件属性ci对对象u存在值f(u,ci)=z，且该值不属于任何其他决策类，则称z为Ud(j)在条件属性ci上的独立决策条件属性值。用Vci(d(j))表示决策类Ud(j)条件属性ci的值域，Vci表示论域U条件属性ci的值域，则独立决策条件属性值满足：

如果ci={z:z∈Vci(d(j),z∉(Vci-Vci(d(j)))}，则f:Ud(j)×{ci:ci=z}∪Dd(j)→Vd(j)成立。——①

2)判断独值集。当决策类Ud(j)条件属性ci存在多个独值时，用集合Zi(d(j))={z1,z2,…,zq}表示，其中z1～zq表示条件属性ci的各个独立条件决策属性值，设为zk∈Vci(d(j))，1≤k≤q；因此，公式①可转变为公式②：

如果Zi(d(j))={z1,z2,…,zq}，且ci={zk:zk∈Zi(d(j)),Zi(d(j)⊆Vci(d(j)),Zi(d(j))⊄(Vci-Vci(d(j)))}，则f:Ud(j)×{ci:ci=zk}∪Dd(j)→Vd(j)。——②

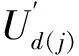
步骤4:复合运算构建的新型多变量决策树算法。完成前3步后的决策类Cd(j)x信息表为Sd(j)=，Ud(j)={u1(d(j)),u2(d(j)),…,un(d(j))}，Cd(j)={c1(d(j)),c2(d(j)),…,cn(d(j))}，|VDd(j)|=1，各分区决策类决策属性值唯一，且信息函数f:Ud(j)×(Cd(j)∪Dd(j))→VDd(j)成立。如论域包含对象m个，Ud(j)对应决策表如表2所示。

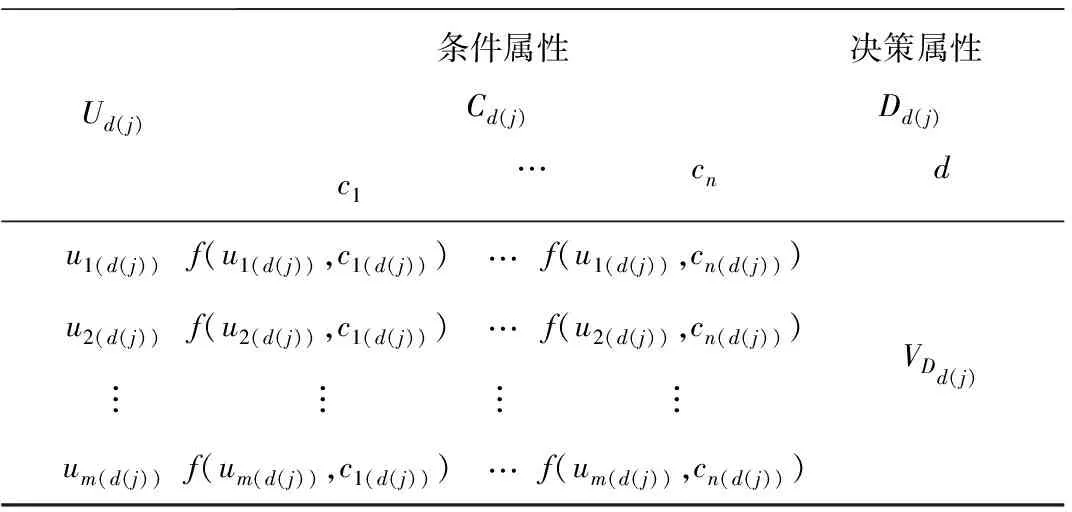
表2 决策表——论域Ud(j)

1)对象分量相交。取表2条件属性集Cd(j)，并用a11～amn表示1～m行(对象)在1～n列(条件属性)的值，下面分别用x和y表示行和列下标。条件属性集为

设tx∈Cd(j)，tx表示第x个对象的条件属性集，tx[ci]则表示对象tx在属性ci的一个分量，ci(d(j))={a1i,a2i,…,ami}，1≤i≤n。

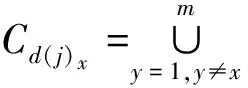
2)删除无效对象。对集合Cd(j)x中的每个对象所包含的属性值进行计数，当计数值小于等于1时，说明该对象的条件属性集无法进行有效决策，从集合Cd(j)x中删除此类对象。

3)判断最优对象近似度。当集合Cd(j)x所包含的有效元素个数越多，则由对象tx条件属性集所产生多变量决策的可能性越高。构建函数MAX(findnonull(Cd(j)x))用于求取Cd(j)x中有效元素个数的属性集。

4)保留最优循环后的多变量决策集合。当Cd(j)1～Cd(j)m中存在多个最大有效元素值相同时，保留这些集合并依次对其执行步骤4的1)～ 3)，直至每个集合最后只剩下单个对象(每循环执行1次，产生的新集合所包含的对象个数减1)。

运算结果可能会保留下多个拥有单个对象的集合，对每个集合执行步骤4的5)～ 7)。

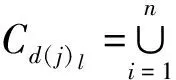
对Cd(j)l元素个数进行计数，并根据不同情况进行处理。

(1)|Cd(j)l|≤1。集合中有效的条件属性值小于等于1时，说明这个集合无法满足多变量决策要求。回溯到求取当前集合的上一集合，回溯后的集合至少包含2条以上的对象条件属性值有效，且每个对象至少包含2个非空分量。将每个对象的条件属性值作为最终集合进行约简，并执步骤4的6)。

(2)|Cd(j)l|≥2。集合中有效元素个数满足多变量决策要求，并执行步骤4的6)。

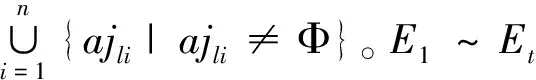
8)循环多变量运算。对论域Ud(j)循环执行步骤4的1)～ 7)直至所有对象完成多变量决策运算，每循环1次至少能获取1条多变量决策逻辑表达式。

9)推导出完整的逻辑表达式。当决策类Ud(j)完成多变量决策运算后可能产生n′个逻辑表达式，分别用condd(j)[1]～condd(j)[n′]表示。设condd(j)为决策类Ud(j)推导后的完整多变量逻辑表达式，则condd(j)=condd(j)[1]∨condd(j)[2]…∨condd(j)[n′]，且使condd(j)→d=VDd(j)成立。

10)判断最优逻辑表达式。当执行步骤4的5)时，如存在多个最优近似度相同集合，由此可能推导出多个有效逻辑表达式，分别用cond1(d(j))～condm′(d(j))表示。设condy′(d(j))表示cond1(d(j))～condm′(d(j))中的第y′个逻辑表达式，1≤y′≤m′。设函数findv(∨,condy′(d(j)))，用于查找condy′(d(j))中所包含的或运算符(∨)的个数，当该函数取值越低时，表示condy′(d(j))逻辑表达式的复杂度越低。保留最小复杂度的逻辑表达式作为最优逻辑表达式。

步骤5:决策表完整的决策规则。对各分区决策类完成上述步骤1～4，设Ud(1)～Ud(p)的独立决策条件属性逻辑表达式为indecondd(1)～indecondd(p)。indecondd(j)表示决策类Ud(j)的独立决策条件属性逻辑表达式，当indecondd(j)=∅时，Ud(j)不存在独立条件属性决策值。论域U独立决策条件属性逻辑表达式为indecond，则indecond=indecondd(1)→Vd(1)∨indecondd(2)→Vd(2)∨…∨indecondd(p)→Vd(p)。

设Ud(1)～Ud(p)的多变量决策逻辑表达式为condd(1)～condd(p)，论域U的多变量逻辑表达式为cond，则cond=condd(1)→Vd(1)∨condd(2)→Vd(2)∨…∨condd(p)→Vd(p)。

合并2部分决策规则取得完整的决策：cond∨indecond。

3 基于决策类划分新型多变量算法实例分析

通过对多个决策树进行算法实例分析，发现本算法是有效的，现以决策树典型训练集——气象信息系统表(表1)为实例进行证明。各步骤运算情况如下。

步骤1:根据决策属性划分论域。对训练集根据决策值进行不可分辨关系划分。因决策属性值域VD={N,P}，将论域U根据决策属性值划分为2个等价决策类。U/ID={{1,2,6,8,14},{3,4,5,7,9,10,11,12,13}}，这2个决策类分别用UN和UP表示。

步骤2:二义性条件属性判断。CN={a1N,a2N,a3N,a4N}，CP={a1P,a2P,a3P,a4P}。因CN∩CP=∅，所以论域U不存在二义性条件属性。

步骤3：独立决策条件属性值的判断和处理方式。求出CN和CP各条件属性值域。将CN与CP相对应条件属性值域进行比较，可见Va1P-Va1N={overcast}。说明a1=overcast→D=P为决策类UP的独立决策条件属性值。将判断为a1=overcast的独立条件属性值相关的对象从决策类UP中删除。

步骤4：获取多变量逻辑表达式。取UN和UP中的条件属性集分别进行分量相交。

由UN推导出的多变量逻辑表达式的最后结果为(a1=0∧a3=0)∨(a1=1∧a4=1)→D=N。

由UP推导出的多变量逻辑表达式的最后结果为(a1=1∧a4=0)∨(a1=0∧a3=1)→D=P。

步骤5：决策表U完整的逻辑表达式。

综上所述，将UN和UP取得的多变量决策规则转换为逻辑表达式，分别为：(outlook=sunny humidity=high) (outlook=rain windy=true)→(class=N)和(outlook=rain windy=false) (outlook = sunny humidity=normal)→(class=P)。

独立决策逻辑表达式为(a1=overcast)→(D=P)，即(outlook=overcast)→(class=p)。

将上述逻辑表达式组合为完整的决策表达式，可得气候集的决策表达式为 ((outlook=sunny humidity=high) (outlook= rain windy=true)→(class=N)) (outlook=rain windy=false) (outlook=sunny humidity=normal)→(class=P)) (outlook=overcast)→(class=P)。将其转换为逻辑语句：

If (outlook=”sunny” and humidity=”high”)or (outlook=”rain” and windy=”true”)Then class=”N”;

If (outlook=”sunny” and humidity=”normal”)or (outlook=”rain” and windy=”false”)or outlook=”overcast” then class=”P”;

由此可见，获得的结果与ID3和粗糙集多变量运算结果无二，证明新决策树构建方法成立。

4 算法复杂度分析与比较

设训练集中有n行记录，m个条件属性，决策值域个数为p，则ID3算法的信息熵的时间复杂度为O(n2log2n)。粗糙集的核心步骤是计算等价类，它的时间复杂度为O(m×n2)[5]。

下面对新算法5个步骤的时间复杂度进行分析。

步骤1采用不可分辨关系依据决策属性值对训练集进行划分，其时间复杂度为O(n)。

步骤2利用决策类之间条件属性集相交是否为空判断训练集是否存在二义性数据，其时间复杂度为O(p2)。

步骤3利用决策类之间的各条件属性值域的不同，判断是否存在独立决策条件属性值，并获取独立决策规则，其时间复杂度为O(m/p)。

步骤4利用一个复合运算方式构造出一种新型的多变量决策方法，能快速获取各决策类的多变量逻辑表达式，并依此推导决策规则，其时间复杂度为O(m×n2/p)。

步骤5使用或运算符(V)将各个独立决策规则和多变量决策规则进行连接，其时间复杂度为O(p)。

本算法的核心部分为第4步骤，取其时间复杂度与ID3算法和粗糙集算法对比。这3种算法对比的关键要素集中在n、m和p这3个参数。在其中1个参数变动，另2个参数保持不变的情况下进行分析，如表3—5所示，取得的实验分析结果如图2—4所示。

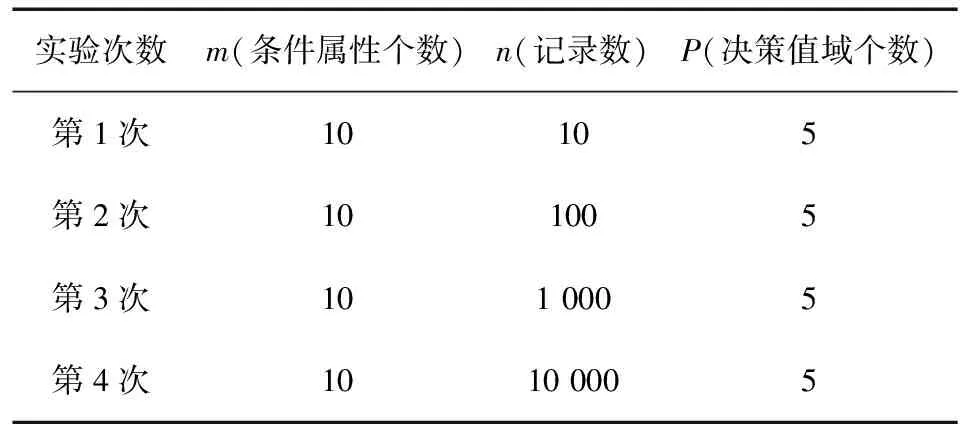
表3 仅记录增长

在条件属性个数和决策值域不变而记录增长的情况下进行分析的结果如图2所示。可知，当记录数增长时，3种算法的运算次数均是增长的，但新算法的增长速度最慢。

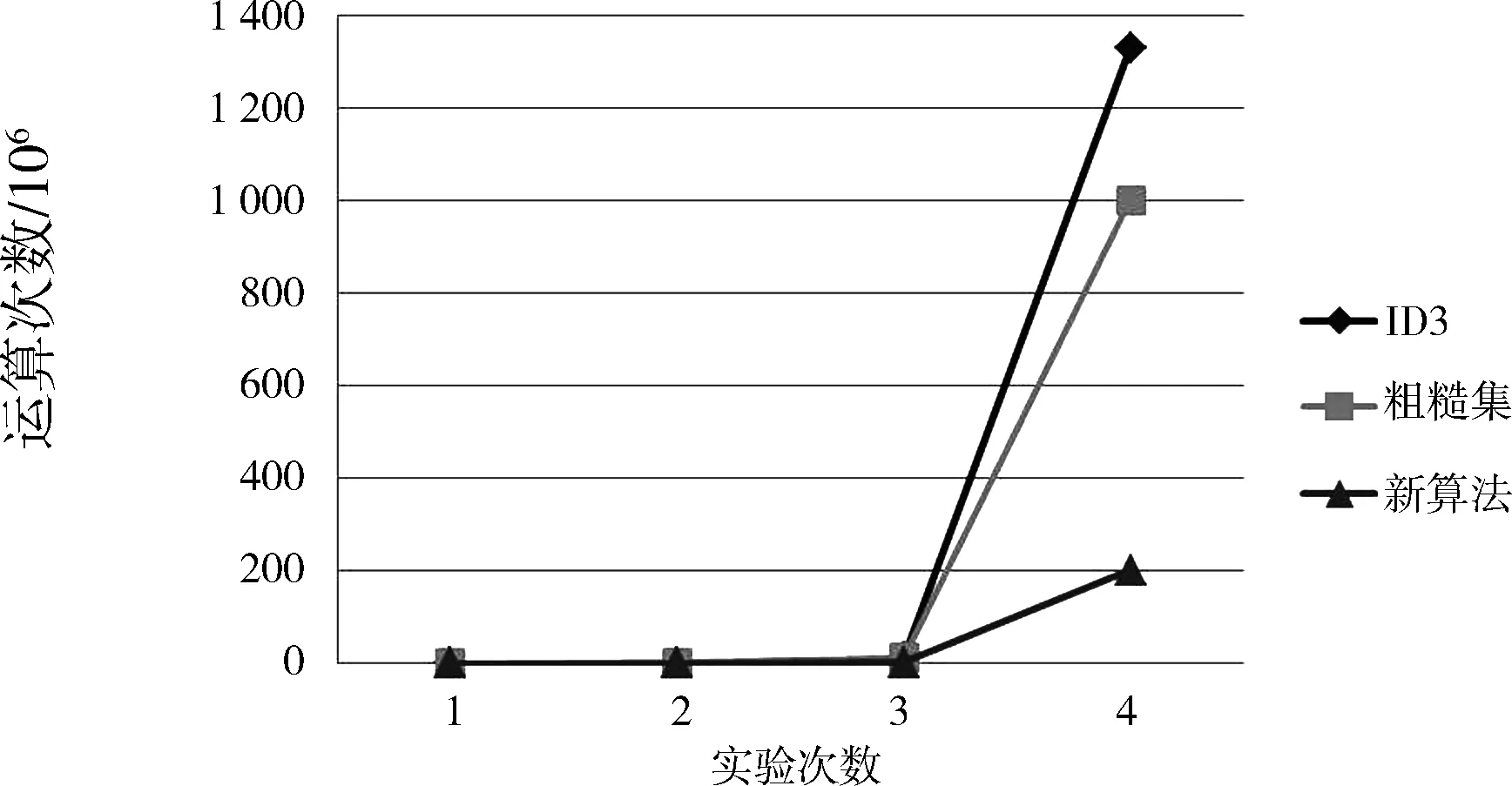
图2 仅记录增长算法分析图

表4 仅决策值域个数增长

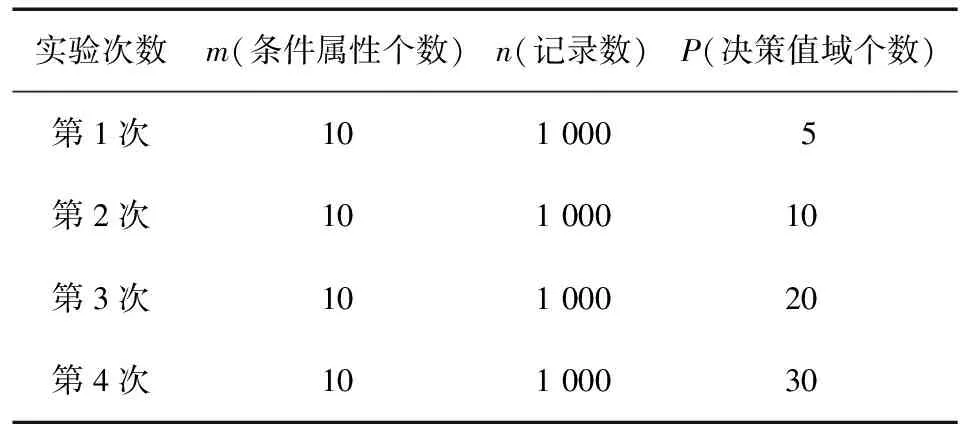
实验次数m(条件属性个数)n(记录数)P(决策值域个数)第1次1010005第2次10100010第3次10100020第4次10100030

在条件属性和记录数不变而决策值域个数增长的情况下进行分析的结果如图3所示。可知，当决策值域个数增长时，ID3和粗糙集这2种算法的运算次数是持衡且相同的(这2种算法的运算次数彼此覆盖)，新算法的运算速度却是降低的。

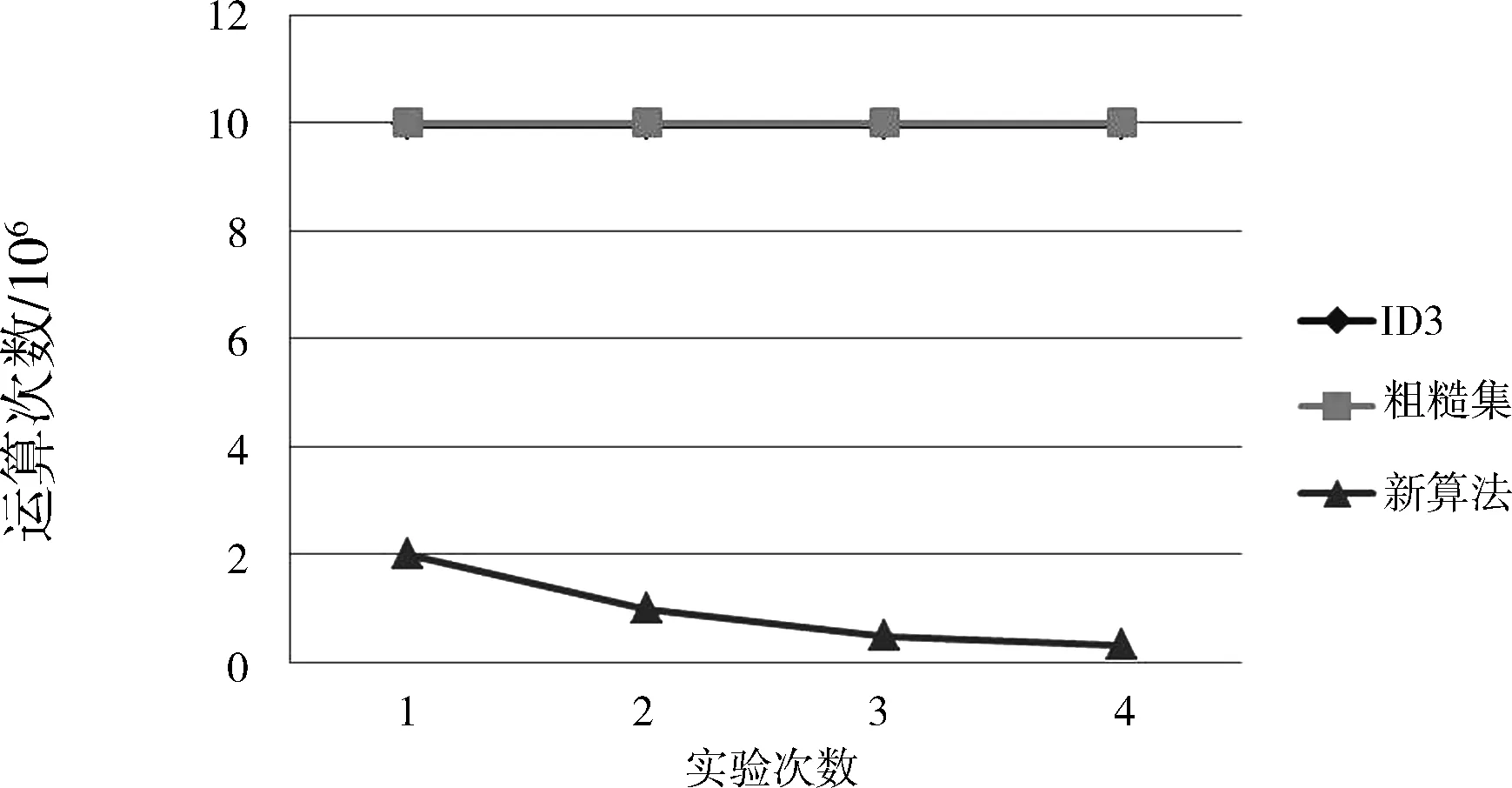
图3 仅决策值域个数增长算法分析图

表5 仅条件属性个数增长

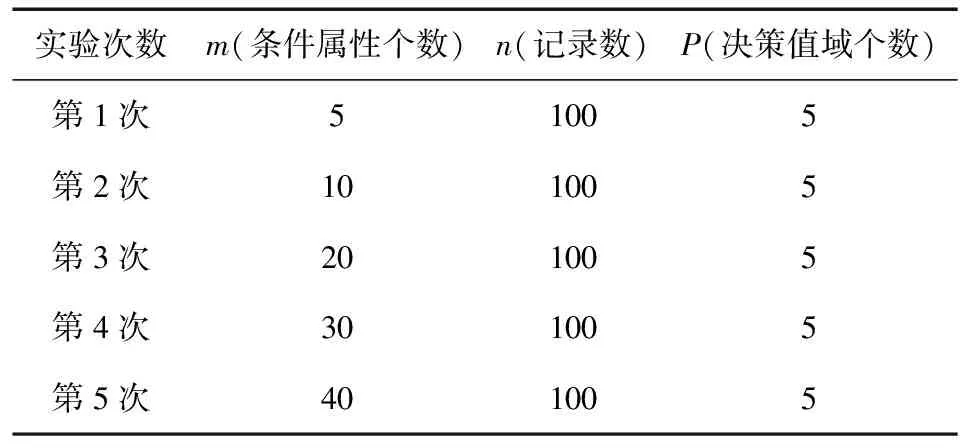
实验次数m(条件属性个数)n(记录数)P(决策值域个数)第1次51005第2次101005第3次201005第4次301005第5次401005

在记录数和决策值域个数不变而条件属性个数增长的情况下的分析结果如图4所示。可知，当条件属性个数增长时，ID3运算次数不变，而粗糙集和新算法的运算次数是增长的，但新算法的增长幅度远低于粗糙集。

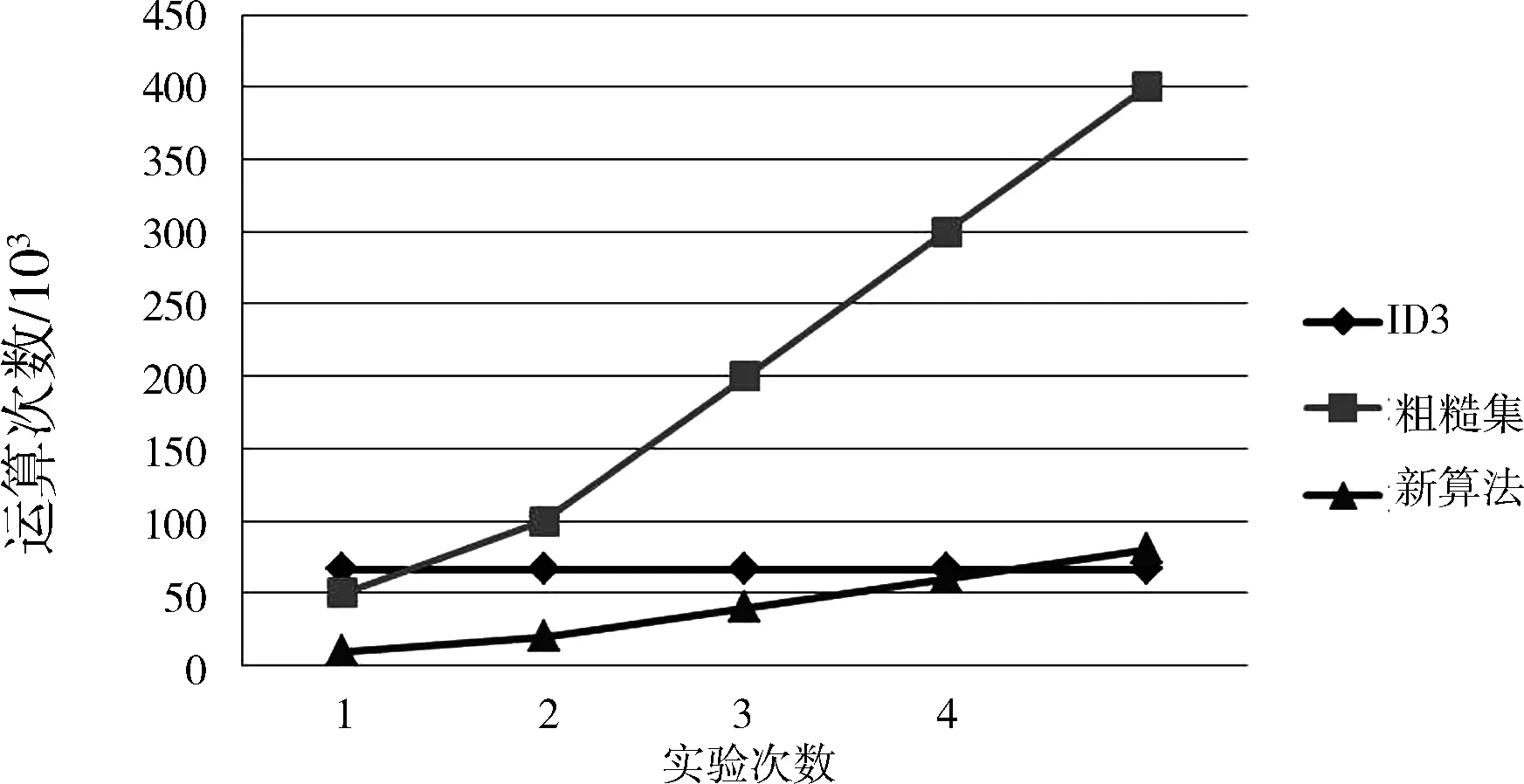
图4 仅条件属性个数增长算法分析图

综上所述：新算法在m、n和p这3个参数分别增长的情况下，其运算速度均远远优于粗糙集算法；当条件属性个数增长且达到一定临界值时，其运算速度会超过ID3算法。

5 结论

本文提出了一种新型的多变量决策树构造算法，该算法有5个步骤：1)采用不可分辨关系依据决策属性值对训练集进行划分，能有效减少后续算法涉及的数据量及其复杂度；2)利用决策类之间条件属性集相交是否为空判断训练集是否存在二义性数据；3)利用决策类之间的各条件属性值域的不同，判断是否存在独立决策条件属性值，并获取独立决策规则；4)利用一个复合运算方式构造出一种新型的多变量决策方法，从而快速获取各决策类的多变量逻辑表达式，并依此推导决策规则；5)使用或运算符(∨)将各个独立决策规则和多变量决策规则进行连接，获取完整的决策规则。通过模拟证明该算法有效，并在时间复杂度方面优于粗糙集，当训练集记录处于增长状况时更优于ID3算法。

[1]Quinlan J R.Induction of Decision Trees[J].Machine Learning,1986(1):81-106.

[2]Quinlan J R.C4.5:Programs forMachine Learning[M].SanMateo.CA:Morgan Kauffman,1993.

[3]苗夺谦,王珏.基于粗糙集的多变量决策树构造方法[J].软件学报,1997,8(6):425-431.

[4]沙惠新,叶东毅.基于知识粗糙集的多变量决策树的构建[J].福州大学学报：自然科学版，2004,32(2):138-141.

[5]吴强,李金龙,杨振宇.基于非线性拟合方程的多变量决策树算法[J].中国科学技术大学学报，2006,36(5):546-549.

[6]Pawlak Z W.Rough Sets[J].Internationl Journal of information and Computer Science,1982,11(5):314-356.

[7]安利平.基于粗集理论的多属性决策分类[M].北京：科学出版社,2008:15-22.

[8]吕映芝,张素琴,蒋维杜.编译原理[M].北京：清华大学出版社,1998:39.

[9]陈建凯,王熙照,高相辉.改进的基于排序熵的有序决策树算法[J].模式识别与人工智能,2014,27(2):134-140.

[10]王鑫,王熙照,陈建凯.有序决策树的比较研究[J].计算机科学与探索,2013,7(11):1018-1025.

[11]许行,梁吉业,王宝丽.基于双向有序互信息的单调分类决策树算法[J].南京大学学报：自然科学版，2013,49(5):628-636.

[12]王萍,张晓丹,张磊.H.264/AVC中基于决策树的P帧快速模式选择[J].中国图像图形学报,2014,19(3):476-483.

[13]王之津,周鹏,韩正彪.基于决策树算法的竞争对手识别模式研究[J].情报理论与实践,2013,36(3):1-6.

[14]陈子春,黄小刚.基于模糊相容关系的集值决策表的相对约简[J].西华大学学报：自然科学版,2012,31(4):31-36.

[15]彭宏,吴铁峰,张东娜，等.粗糙模糊模型及其在入侵检测中的应用[J].西华大学学报：自然科学版,2005,24(3):1-3.

[16]谢小林.基于ID3算法的道路客运行业信用评级模型[J].西华大学学报：自然科学版，2007，26(1)：25-27.

(编校：饶莉)

ANewMultivariatetheDecisionTreeAlgorithmBasedontheDecisionClassification

HUANG Jun-nan

(QuanzhouVocationalCollegeofEconomicsandBusinessInformationDepartment,Quanzhou362000China)

A new multivariate decision tree algorithm is proposed based on the conceptions of indiscernibility relation, compound operations, set operations and logical operation in set theory. It consists of five steps. Firstly, decision is classed according to the decision attribute value. Secondly, the attribute value is worked out according to the set intersection of the decision classes condition attribute. Thirdly, the independent decision condition attribute values are obtained according to each condition attribute field of the decision classification. Fourthly, multivariable decision rules are find out with compound operations of the decision classe condition sets. Finally, the OR operation is used to connect every decision rule in order to produce a complete rule. Experiment results demonstrate that the algorithm is effective. The time complexity results demonstrate that this algorithm has better time performance than rough sets algorithms, and no less than ID3 algorithm indeed.

univariate decision tree; multivariable decision tree; decision table; set operation; logic operation

2014-11-15

福建省教育厅科技项目(JB13357)。

黄俊南(1977—)，男，讲师，硕士，主要研究方向为数据库、算法分析、系统分析。

TP301.6

：A

：1673-159X(2015)03-0006-07

10.3969/j.issn.1673-159X.2015.03.002