“物理模型一题多问”彰显物理之美
(新疆兵团二中 新疆 乌鲁木齐 830002)
何 勇 陈奕琪
作为教师,我们在传授基础知识,指导学生掌握物理规律的同时,也要注意提高学生分析问题和解决问题能力、探索和思维的习惯,努力把他们培养成富有科学创新性的人才.对于一个物理模型,我们可以结合教学进度和学生的理解能力创设多个问题,使物理模型显现出它独特的魅力.
现就以“单导棒模型”、“子弹打木块模型”为例,创设一题多问,从不同角度对物理模型的理解,实现对知识的高度整合和灵活应用.
1 对比式提问
【模型1】现有两根足够长的直金属导轨平行放置,中间接有一定值电阻R(除电阻R外,其余各处电阻均忽略不计),装置处于匀强磁场B中,一根质量为m的均匀金属杆放在两导轨上,现对其施加一个水平向右的拉力F,大小和方向恒定,试分析均匀金属杆的运动情况?

图1
分析:金属杆运动,产生感应电流,金属棒受到的安培力对其运动有阻碍作用,根据牛顿第二定律可得

由此可得,金属棒做加速度减小的加速运动.在起始时金属棒的加速度最大,大小为;当F=F安时,达最大速度随后做匀速直线运动.
问题:如果将电阻换成电容器,如图2所示,其余条件不变,那么金属杆的运动情况又将如何呢?

图2
分析:金属棒在水平面上仍旧只受到拉力F和安培力F安的作用.
根据牛顿第二定律可得

由于在运动过程中,感应电动势不断变化,因此采用微元法,取极短的时间Δt进行研究

根据式(1)~ (3)得
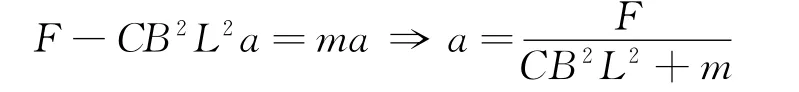
式中F,B,L,C,m都为常量.
因此,金属棒运动的加速度是恒定的,由此可得出金属棒在运动过程中一直做匀加速运动.
2 递进式提问
【模型2】如图3所示,已知子弹质量为m,水平初速度为v0,射入一质量为2m,长度为L的木块,设子弹射入木块过程中,相互作用力为恒力,子弹尺寸和空气阻力忽略不计.
问题1:若木块固定时,子弹恰好射穿.那么木块放在光滑平面上不固定时,子弹能否射穿?子弹射入深度大还是木块位移大?在相互作用力一定的情况下,木块的质量越大,子弹射入深度是否越大?时间是否越长?

图3
何 勇 陈奕琪
分析:面对如此多的问题,其实他们都是与运动学相关的问题,可以用一个方法解决——图像法.
解析:由于“子弹和木块”的相互作用为恒力.如果将两个物体运动情 况 画 在 同 一 “v-t”图中,如图4所示.当木块固定时,子弹恰好射穿,深度L=S△AOC;当木块不固定时,在B点共速,射入深度d=S△AOB<S△AOC,所以射不穿;而木块的位移s=S△OBE<S△OAB=d,木块位移小于子弹深度;当木块质量增大,则木块的加速度就越小,即“v-t”图线斜率越小,由OB向OB′,OB″变化,可看出深度S△OAB<S△AOB′<S△OAB″(深度会增大),时间t1<t2<t3(时间会越长).
问题2:一颗质量为m的子弹以初速度v0穿过在光滑水平面静止的两木块,所经历的时间为t1和t2,设子弹在木块中的阻力恒为F,两木块分别为mA和mB,则最终子弹和木块速度多大?

图4
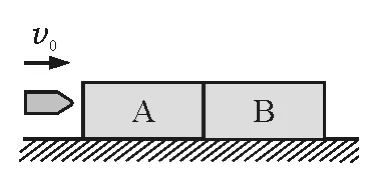
图5
解析:在子弹射穿第一块木块过程中,对“A和B”研究,由动量定理得

在当子弹在射穿第二块木块过程中,对“B”研究,由动量定理得

在子弹射穿木块全过程中,对“子弹”研究,由动量定理得
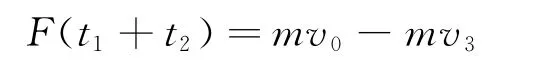
问题3:如图6所示,在光滑的水平面上的木块A的右端用轻弹簧再连接一质量为2m的木块B.若子弹射入木块A后留在里面,那么弹簧具有的最大弹性势能和B的最大速度为多少?

图6

图7
分析:子弹在射入木块A后留里面的过程时间极短,我们可以认为瞬间完成,并且达到共同速度.此后的运动就较为复杂些了,因为A,B的运动均为变加速运动,我们可以做出A,B的“v-t”图.
解析:(1)子弹与木块A共速后,压缩弹簧,B加速,A和子弹减速;
(2)当A,B共速时,弹簧压缩量最大,弹性势能最大;
(3)处于压缩的弹簧,之后使B加速,A减速,B速度大于A速度,压缩量减小;
(4)当弹簧恢复原长时,B速度最大;
(5)接着弹簧被拉伸,B做减速运动,A开始加速;
(6)当A,B达到共同速度时,弹簧拉伸至最长;
(7)处于拉伸状态的弹簧,之后使B继续减速,A加速,且弹簧逐渐恢复原长;
(8)当B速度为零时,恢复为初始状态;此后,各木块循环运动.
根据以上分析,由动量守恒得
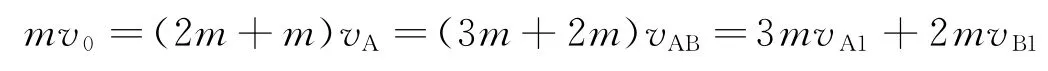
当子弹打入A后,由能量守恒得

根据上式解得

在平时的教育、教学过程中,我们可以通过给“物理模型”设置“对比式”、“递进式”的“一题多问”,有时甚至“一题多解”、“一题多变”等,加强学生对物理现象、知识、规律,以及物理本质的理解,彰显物理之美,而使我们的教学效果达到意想不到的效果.

