对高中数学教材二次开发的新视角、新思维

陈祥国

《高中数学课程标准》明确指出：教材是实施课程目标，实施教学的重要资源.教材应当有利于调动教师的积极性，创造性地进行教学;有利于改进学生的学习方式，促进学生主动地学习和发展.但是限于教材的篇幅，编者对问题的设计意图无法完全暴露，这就需要我们高中数学教师认真研究教材，对教材进行“二次开发”，让教材更有利于学生对知识的理解和思维的发展.

笔者认为高中数学教材二次开发的宝库之一是课本习题，现在以课本的一组习题谈谈“教材二次开发”的新视角、新思维，若有不当敬请指正.

题目 （高中数学必修一，241函数的零点，P72练习题B）

1.求下列函数的零点，并画出函数的图象：

（1）f（x）=2x+7;

（2）f（x）=2x2-5x+1;

（3）f（x）=（x-1）（x-2）（x+3）.

1 承上启下，做好教材新旧知识的过渡与整合

通过此组题目巩固了函数零点的定义与求法，题目虽然简单，但体现了函数与方程思想、数形结合思想，是非常有价值的“二次开发”.

解析 （1）（2）（3）题图象分别为图1，图2和图3：

图1     图2     图3

借此机会大胆地整合教材，做好新旧知识的过渡，引出下节课242“变号零点”的定义：如果函数图象通过零点时穿过x轴，则这样的零点为变号零点.让同学们讨论“变号零点”的性质，同时类比“变号零点”的定义给出“不变号零点”的定义，并举例说明.这样使平淡乏味的问题变得有趣味了，同学们各抒己见，很轻松地解决了新问题.“不变号零点”就是没有穿过x轴的零点.

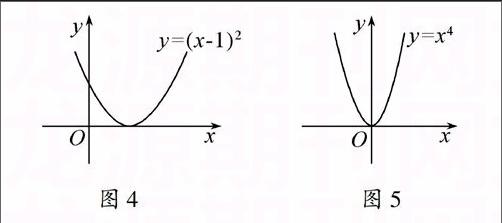
例如函数y=（x-1）2，y=x4等.

图象如图4和图5所示：

图4         图5

从数（定义）和形两个角度总结出零点的分类及性质，学生学习情绪高涨，真所谓“深深的话，浅浅地说”，浅显易懂.

因此，用好教材要以知识的连续性和学生认知的实效性为标准，这就需要我们每位教师认真分析教材，对教材的“二次开发”要有新视角、新思维，站在整体高度审视教材，大胆地整合教材，做到层次分明，结构清晰，让不同领域的知识交汇成一个系统.

2 引申拓展，寻找知识间的规律

利用这组题目设疑：“同学们，借助零点（变号零点和不变号零点）能否画出下列函数的图象？”

引申 画出下列函数图象：

（4）y=（x-1）2（x-2）（x+3）;

（5）y=（x-1）3（x-2）2（x+3）.

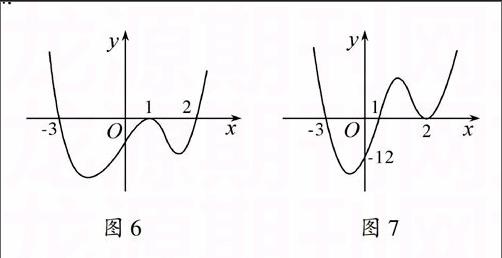
分析 （4）1是不变号零点，2，-3是变号零点，如图6所示;

（5）2是不变号零点，1，-3是变号零点.如图7所示.

图6         图7

师生共同总结规律如下：

1.分解因式求零点（x的系数为1）;

2.在x轴上从小到大标零点;

3.从右上方穿零点（奇过偶不过）.

“奇过偶不过”就是因式的奇次方对应的零点是变号零点，所以既穿又过;因式的偶次方对应的零点是不变号零点，所以只穿不过.

利用这组题目的拓展引申，归纳总结出一类“一元高次多项式函数”图像的画法，使同学们豁然开朗，体会到函数零点在画图像中“神奇”的重要作用，从而可以结合函数图像来研究函数的性质了.

数学是高中课程中的一门主要学科，课时最多，内容浩瀚，记忆和掌握起来都比较困难.所以我们要重视教材的“二次开发”，站在系统的高度上注意比较知识间的区别和联系，不但有利于抓住问题的本质，而且可以找出规律即共性，简化记忆，便于掌握.

3 变式应用，训练学生的思维能力

分析教材（P72练习B）两组题目很易得出其设计意图，利用函数图像来求解不等式.承接上述知识进行设疑，以达到训练学生思维的目的.

变式 解下列不等式：

（1）2x+7>0;

（2）2x2-5x+1≤0;

（3）（x-1）（x-2）（x+3）>0;

（4）（x-1）2（x-2）（x+3）<0;

（5）（x-1）3（x-2）2（x+3）≥0.

在大家熟悉的题目（1）（2）的启发下，学生们很容易联想到利用图像来解决不等式问题，顺水行舟，触类旁通，（3）（4）（5）就很容易解决了.

解析

由图象写出解集：

（3）的解集是{x|x>2或-3<x<1}，图8;

（4）的解集是{x|-3<x<2且x≠1}，图9;

（5）的解集是{x|x≥1或x≤-3}，图10.

图8     图9     图10

借助函数零点画出图像，一元高次不等式就轻松解决了，也就是“穿根法”.其解法实质是数形结合思想的应用，体现了高中数学中最重要的数学思想方法之一：函数、方程、不等式的转化.因而在教学中要加强数学语言的转化训练，培养这种意识，做到“胸中有图”，“见数思图”，以开拓学生的思维.

以课本的知识为载体，以层层设疑来达到知识的深化，从而提炼方法，总结规律，训练学生的思维能力.一组简单的题目却传递着“巨大的能量”，这需要我们每位教师在备课时做个“有心人”，在研究教材时做个“用心人”，开辟新的视角进行多维度的再开发，激发学生思维，让学生的能力在开发中获得更多的提升.

4 传递情感，激发学生学习数学的兴趣

通过对课本习题的“二次开发”，将一组看似简单的题目变得“深奥而富有生机和活力”，使课堂的“数学味”越来越浓，营造了良好的情感氛围.在课堂中对开发的问题使用“开放式”提问，“你发现了什么？”“谁起来说说自己的想法？”等等.让学生充分自由大胆地表述、质疑、探究、讨论，让学生体验数学思考的酸甜苦辣，享受智力活动的振奋与愉悦.在课堂上，笔者借助这一类函数的图象总结：“数学是美丽和谐的，我们的人生就像今天所研究的图像一样，曲曲折折，有上升也有下落，但我们一定要勇往直前（上升）……”.

随着人们对高效课堂的追求与新课程的深入推进，数学教材的二次开发越来越受重视，更重要的是学生因为开发而思考，课堂因开发而精彩，教师因开发而发展，教材因为开发而丰满，数学因开发而有趣.用新视角、新思维开发教材是一种境界，我们当继续努力！