一道无理函数值域问题的变式探究
2015-07-12 07:23邱明武
新课程(中学) 2015年10期
邱明武
(江西省信丰县第七中学)
函数值域的求法是高中函数教学中的重点,同时也是难点,其常用方法有:观察法、反函数法、分离常数法、配方法、换元法、判别式法、不等式法、单调性法、求导法、函数的有界性法、数形结合法等等.这道题主要考查无理函数值域的求法,而无理函数值域的常用求法有:单调性法、反函数法、配方法、换元法、求导法、数形结合法、构造解析几何模型法等。首先来探究一下本题的解决方法,如下:
解法1(单调性法)
解法2(反函数法)
这道题的两种解法平时教学多次渗透,学生也知道求值域的一些基本方法,但就是用起来达不到应用自如、熟能生巧、举一反三的地步.观察这道题的结构,不难联想到这道题的变式题又如何求解?下面就让我们来探究一下这道题的变式求解吧.
评注 这道题虽含根式看似很复杂,但若分析其单调性来求值域就很简单了.因此对某些求函数的值域或最值问题,可以从函数的单调性角度来考虑.
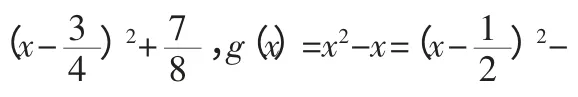
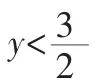
猜你喜欢
小猕猴学习画刊(2022年3期)2022-03-28
新世纪智能(数学备考)(2021年9期)2021-11-24
石家庄铁路职业技术学院学报(2021年1期)2021-06-09
快乐学习报·教师周刊(2021年37期)2021-02-07
新世纪智能(数学备考)(2020年9期)2021-01-04
中学生数理化·高一版(2018年10期)2018-11-08
祖国(2018年3期)2018-03-26
理科考试研究·高中(2017年10期)2018-03-07
课程教育研究·学法教法研究(2016年27期)2017-04-21
小学阅读指南·低年级版(2017年2期)2017-03-23

