一种动态面自适应滑膜控制策略*

高春燕

(陕西青年职业学院，陕西 西安 710068)

一种动态面自适应滑膜控制策略*

高春燕

(陕西青年职业学院，陕西 西安 710068)

针对传统算法存在的难以满足控制系统要求的问题，设计了一种动态面自适应滑膜控制策略，通过构建新切换函数并求导，得到了连续的动态滑膜控制律，最后通过仿真和试验结果，验证了该方法在鲁棒性和抖振方面具有较好效果。

自适应控制；非线性；不确定性；仿真；鲁棒性

滑膜控制作为一类非线性控制，具有响应速度快、对参数及扰动不灵敏、鲁棒性强和物理实现简单等优点，被广泛地应用在智能控制领域当中；但是，其具有非线性、不确定并带有干扰的缺点，为解决上述问题，提出通过采用智能控制的方法，如神经网络算法和模糊规则等对电动机伺服系统进行控制。为了解决抖动问题，有学者提出采用积分切换控制律的方式，加入切换函数积分的绝对值，从而使得其增益量近似为 0，以达到削弱抖振的目的。对此，本文提出在构建切换函数的基础上，得到连续动态自适应动态滑膜控制律，从而达到消除抖振和干扰的目的。

1 滑膜控制理论

对滑膜控制的核心可以概括为：首先，通过控制目标的运动轨迹，设计一个可达到稳态的目标滑膜面；然后，对滑模面的不同侧运动确定其空置率，从而得到使其中各个点都趋于平衡的滑模面运动，并达到稳定的状态[1]。根据轨迹的不同，通常可以将滑模面不同侧的这些运动点分为3类，即起始点、通常点和终止点。滑模运动示意图如图1所示，A表示起始点；B表示通常点，C表示终止点。

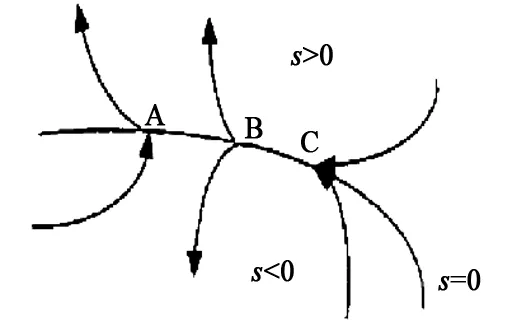
图1 滑模运动示意图

通过上述控制思想可知，滑膜控制主要还是针对终止点，根据该空间状态内的各个点无论处在任何一个滑膜面，都通过控制律算法使其沿着滑膜面s(x)=0进行运动，从而达到比较稳定的状态。同时，通常情况下，在滑膜运动的过程中，可对其中的滑膜面s(x)及其控制律U进行设计，设计目的是让滑膜避免在不同侧都存在一个s(x)，从而在控制律U的情况下都可达到s(x)，其速度的方向就是滑膜运动的方向，也就是说滑膜控制中只需要掌握s(x)和U即可实现在参数变化和外界扰动的情况下，其运动不受到任何的干扰[2-4]。因此，滑膜控制存在着很强的抗干扰能力，该控制过程通过数学模型可以描述为：

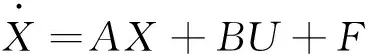
(1)

滑膜面为：

s=s(x)s∈Rm

(2)

设定好的控制律为：

(3)

在实际应用当中，对滑膜面的设定和对控制律的选取都有着各自的方法，其不同的组合方式被应用在不同的控制条件之下。根据对滑膜控制过程的描述可得，只要满足滑模面的存在性、可达性以及滑模运动的稳定性，即可通过滑膜实现控制。

2 控制系统问题的数学描述

假设该控制系统为高阶非线性系统，因此有：

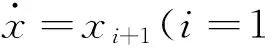
(4)式中，μ∈R，是系统控制输入；x=[x1,x2,x3,...,xn]T∈Rn；f(x)是系统的非线性的动态函数；v是辅助项，用于对动态控制律的设计；θ是误差。

式4表示该系统为非线性、不确定系统，包含着n个不确定的参数，建议其中的x>0并且不断递增。

3 自适应动态滑膜控制器设计

结合上述滑膜控制理论，首先要构造滑膜控制面。根据相关的计算流程，本文将该切换函数的公式定义为：

(5)

本文主要对设计的第1步进行了介绍，后续的步骤依此类推。将式5带入式1可以得到：

(6)

定义其中的Lyapunov函数，则有：

(7)

对式7进行求导得：

(8)

将x2作为虚拟控制输入，则存在一个期望的反馈控制函数：

x2=-λx1

(9)

式中，λ为常数，其值大于零，则有：

(10)

同理对步骤2进行计算和定义。

在第i步的时候，有i=3,…,n-1，对其以此类推，则有定义Lyapunov函数V3,V4,…,Vn-1，因此在第n步有：

(11)

对式11进行求导得到：

(12)

对此，令其动态滑膜控制律为：

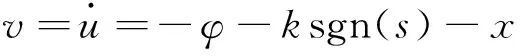
(13)

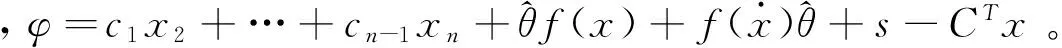
由此可以得到：

(14)

将式14带入式11中可以得到：

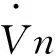
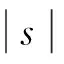
(15)

取其自适应率为：

(16)

将公式16带入式15可得到：

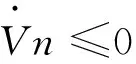
因此，通过上述分析可以得出李雅普诺夫定理，并且得到其在有限的时间之内将直接收敛到0，由此可以得出，该自适应控制方法的动态控制律可很好地实现在不确定性的条件下的动态滑膜控制，并且其抖振效果明显[5]。

4 算法验证

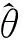
图2 系统响应时间

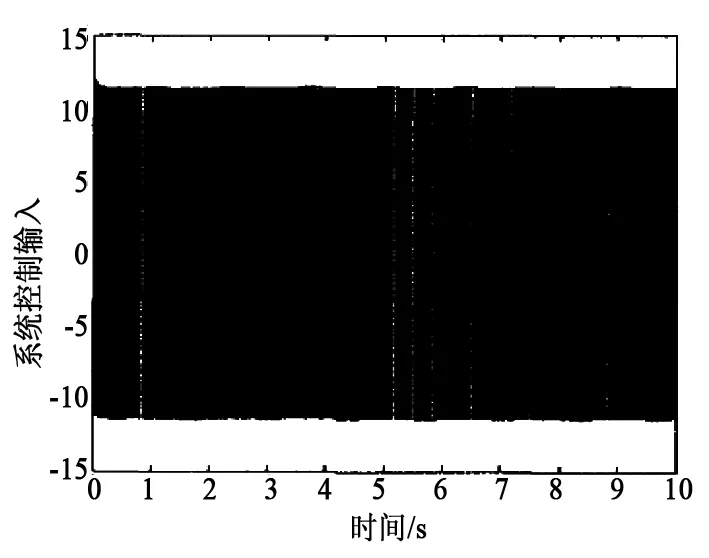
图3 常规滑模控制器控制量输出

5 结语

通过上述对算法的验证可得到其在稳定性和响应速度方面都有着非常明显的效果，并且在抖振效果方面也非常明显，由此证明该算法科学、有效，值得推广应用。

[1] 邓玮,孙君曼,崔光照,等. 基于非线性输入控制实现受扰混沌系统同步[J].系统工程与电子技术,2010,4:837-841.

[2] 吴宝举,李硕,王晓辉.自治水下机器人自适应滑膜控制[J].机械设计与制造,2010,7:142-144.

[3] 夏晓南,张天平.具有未建模动态系统的自适应动态面输出反馈控制[J].控制与决策,2014,12:2129-2136.

[4] 杨维，吴德君.模糊控制在工业机器人中的应用研究[J].新技术新工艺，2014(11)：97-99.

[5] 刘霞.基于PLC的双容液位控制系统设计研究[J].新技术新工艺，2013(2)：115-117.

责任编辑李思文

AControlStrategyforDynamicSurfaceAdaptiveSlidingMode

GAO Chunyan

(Shaanxi Youth Vocational College, Xi′an 710068, China)

Based on the problem of traditional algorithm are difficult to meet the requirement of control system, a dynamic surface adaptive synovial control strategy was designed, by constructing a new switching function, and through the derivation, dynamic synovial continuous control law was gotten, finally, the simulation and experimental results verified the effects of method in terms of robustness and chattering.

adaptive control, nonlinear, uncertainty, simulation, robustness

G 804.66

：A

高春燕(1980-),女,硕士,讲师,主要从事计算机应用和教学等方面的研究。

2015-01-04