由Noor积分算子刻划的多叶函数子类

华 芳, 束永祥

(镇江高等专科学校 丹阳师范学院,江苏 丹阳 212310)

由Noor积分算子刻划的多叶函数子类

华 芳, 束永祥

(镇江高等专科学校 丹阳师范学院,江苏 丹阳 212310)

用Noor积分算子刻划p叶星象函数、p叶凸象函数的新子类,建立包含关系。

p叶星象函数;p叶凸象函数;Noor积分算子。

在复分析中,自20世纪70年代以来,随着卷积理论的应用,许多学者应用卷积构造出多个算子,研究了解析函数和亚纯函数。近年来,许多学者[1-5]相继引进并研究了与Noor 积分算子有关的各种解析函数类和亚纯函数类。本文利用Noor积分算子定义了多叶解析函数的新子类,建立了包含关系。

1 引言

本文,我们总假定

U={z:|z|<1},

0≤α<1,设Ap表示具有形式

(1)

p∈N={1,2,3,…},且在U内解析的全体函数组成的函数类,若函数

f(z)∈Ap

满足

(2)

(z∈U),则称f(z)为α阶p叶星象函数,记作

若函数

f(z)∈Ap

满足

(3)

(z∈U),则称f(z)为α阶p叶凸象函数,记作

f(z)∈Cp(α)。

对于

f(z)∈Ap,

g(z)∈Ap

且

(4)

p∈N={1,2,3,…}，定义f(z)与g(z)的Hadamard积(卷积)

(5)

对于任意大于-p的整数n,定义函数

使得

(6)

对于

f(z)∈Ap,

定义1个算子

(7)

由式(7)可见

Ipf(z)=f(z)，

由式(7)还可以得到

z(In+pf(z))′=(n+p)In+p-1f(z)-nIn+pf(z)，

(8)

z(In+pf(z))′=In+p(zf′(z))。

(9)

算子In+p-1f(z)是由LIU[5]等给出的,Noor等定义了当p=1时的算子In,并做了研究。

用算子In+p-1f(z)可以刻划新的解析函数类:

Cp(α,n)={f(z)∈Ap:In+pf(z)∈Cp(α)}。

可得

本文建立了上述两个函数类的包含关系。

引理1[6]非常数函数ω(z)在U中解析,且

ω(0)=0,

若

z0∈U,则存在k≥1,使得

z0ω′(z0)=kω(z0)。

2 主要结论

定理1

证明设

置

(10)

这里ω(z)在U内解析,且

ω(0)=0,

从式(8)可得

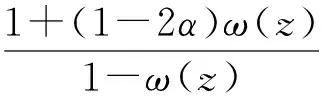
(11)

式(11)两边取对数得

ln(n+p+1)+ln(In+pf(z))-ln(In+p+1f(z))=

ln{(n+p+1)+[p(1-2α)-n-1]ω(z)}-ln(1-ω(z))

(12)

式(12)两边微分得

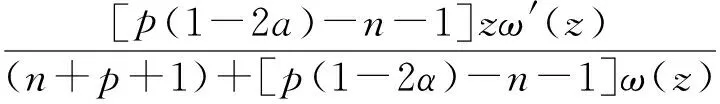
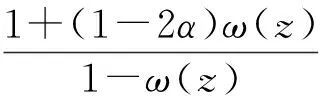
(13)

下面证明

|ω(z)|<1

(z∈U)。

若存在

z0∈U,

使得

由引理1,有

z0ω′(z0)=kω(z0),

k≥1,不妨设

ω(z0)=eiθ,

代入式(13)计算得

{[p(1-2a)-n-1]k(cosθ+isinθ)

{(n+p+1)+[p(1-2α)-n-1](cosθ-isinθ)}}·

{{(n+p+1)+[p(1-2a)-n-1]cosθ}2+

[p(1-2α)-n-1]2sin2θ}-1}=

k[p(1-2a)-n-1]Re{{(n+p+1)cosθ+

[p(1-2a)-n-1]+i(n+p+1)sinθ}·

{(n+p+1)2+2(n+p+1)[p(1-2a)-

n-1]cosθ+[p(1-2a)-n-1]2}-1}=

{(n+p+1)cosθ+[p(1-2a)-n-1]·

(n+p+1)2+2(n+p+1)[p(1-2a)-

n-1]cosθ+[p(1-2a)-n-1]2}-1=

-2p(1-a)k(pα+n+1)·{(n+p+1)2+

2(n+p+1)[p(1-2a)-n-1]

cosθ+[p(1-2a)-n-1]2}-1≤0。

这与

矛盾,故

|ω(z)|<1

(z∈U)。

设

ω(z)=k1(x,y)+ik2(x,y),

再由式(10)得

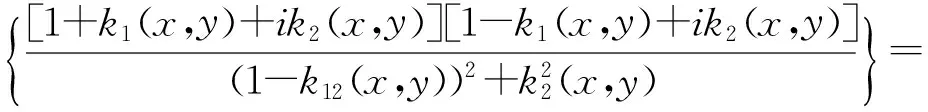
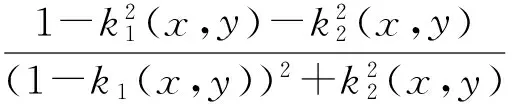
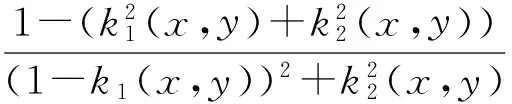
可得

证毕。

定理2

Cp(α,n)⊂Cp(α,n+1)。

证明

f(z)∈Cp(α,n) ⟺

f(z)∈Cp(α,n+1)。

证毕。

[1] CHO N E,KIM I H,SRIVASTAVA H M.Sandwich-type theorems for multivalent functions associated with the Srivastava-Attiya operator[J].Appl Math Comput,2010,217(2):918-928.

[2] WANG Z G,LI Q G,JIANG Y P.Certain subclasses of multivalent analytic functions involvingthe generalized Srivastava-Attiya operator[J].Integral Transforms Spec Funct,2010,21(3):221-234.

[3] AOUF M K,SEOUDY T M.Some preserving subordination and superordination of analytic functions involvingthe Liu-Owa integral operator [J].Comput Math Appl,2011,62(9):3575-3580.

[4] SHANMUGAM T N,JEYARAMAN M P.On sandwich theorems for certain subclasses of analytic functionsassociated with Dziok-Srivastava operator [J].Taiwan J Math,2009,13(6B):1949-1961.

[5] LIU J L,OWA S.Properties of certain integral operator[J].Int J Math Math Sci,2004,3(1):351-359.

[6] JACK I S. Functions starlike and convex of order α[J].London Math Soc,1971,3(2):469-474.

〔责任编辑： 卢 蕊〕

SomesubclassesOfp-valentfunctionsdefinedbyNoorlinearoperator

HUAFang,SHUYong-xiang

(Danyang Normal School, Zhenjiang College, Danyang 212310, China)

Some new subclasses of p-valent starlike functions and p-valent convex functions defined by Noor linear operator were introduced and studied and inclusion relations were established.

p-valent starlike functions; p-valent convex functions; Noor linear operator.

2015-01-02

华 芳(1972—),女,江苏镇江人,副教授,硕士,主要从事数学教学研究;束永祥(1972—),男,江苏丹阳人,副教授,硕士,主要从事数学教学研究。

O174.51

： A

：1008-8148(2015)02-0052-03