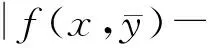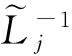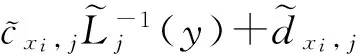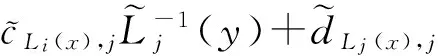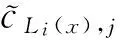一类分形插值曲面的构造方法
孙秀清
(江苏联合职业技术学院镇江分院 基础部,江苏 镇江 212016)
一类分形插值曲面的构造方法
孙秀清
(江苏联合职业技术学院镇江分院 基础部,江苏 镇江 212016)
主要介绍矩形域上一类分形插值曲面的构造方法,并对分形插值曲面的连续性进行严格的证明。
仿射分形插值函数;压缩因子 ;分形插值曲面
1986年,Barnsley[1-2]基于迭代函数系理论首先提出了分形插值函数的概念,它为数据拟合、函数逼近和计算机应用等提供了一种新的工具。多年来,许多学者对分形插值曲面的构造方法展开了广泛讨论,现有文献已经做了很多的工作,取得了丰硕的成果。文献[3]构造了在三维空间里一类多参数分形插值曲面。文献[4]构造了一例分段连续系统,并用迭代函数系来表示,进而研究它的分形特征。以上研究在迭代函数系中使用的都是常数压缩因子。文献[5]研究了一类分形插值曲面的中心变差,为这类分形插值曲面的分形维数的计算提供了基础。文献[6]考虑了多边形区域上过任意插值点的自仿射分形插值曲面。文献[7]证明了,在矩形区域上,当边界插值点共线时,迭代函数系的不变集是连续的插值曲面。文献[8]构造了有相同压缩因子的迭代函数系, 提出了等距插值时新的构造分形插值函数的方法。文献[9]构造了一类具有函数垂直尺度因子的迭代函数系,这类迭代函数系与传统迭代函数系相比,在生成分形插值曲面时更加方便,对插值结点要求的条件也更简单。事实上,这些构造方法都给出了一些限制条件,如插值点共线、压缩因子相等,Dalla[10]解除边界插值节点共线和压缩因子相等的限制,给出了一种新颖的构造方法。本文所研究的分形插值曲面的构造方法,放宽了边界插值结点、压缩因子相等这些限制条件,使得插值方法更加灵活,分形插值曲面的应用更具灵活性和普适性。
1 仿射分形插值函数
给定闭区间
I=[a,b]。
令
{(xi,yi):i=0,1,…,m}
是I×R上的插值结点集,m∈N+且m≥2。其中
a=x0 是I的1个分划。定义线性映射 Li(x)=aix+bi, 满足条件 Li(a)=xi-1, Li(b)=xi, s=max{|Si|:i=1,2,…,m}<1 叫做垂直压缩因子,我们定义映射 I×R→R, Fi(x,z)=siz+cix+di, 满足条件 Fi(a,z0)=zi-1, Fi(b,zm)=zi, 其中i=1,2,…,m。我们得到仿射映射I×R→I×R: (1) 其中 (2) 且i=1,2,…,m,则构成1个插值结点是 {(xi,zi):i=0,1,…,m} 的迭代函数系 {I×R;ωi,i=1,2,…,m}。 (3) 根据参考文献[1-2],我们可以得到下面的定理。 定理1设{I×R;ωi,i=1,2,…,m}是双曲迭代函数系,则存在唯一的不变集 K⊂R2。 它是I上f的连续函数的图像,插值结点集是 {(xi,zi):i=0,1,…,m}。 即 K={(x,z):z=f(x),x∈I}, 其中 f(xi)=zi, i=0,1,2,…,m。如果 并且插值结点不在1条直线上,那么K的计盒维数就是满足方程 (4) 的唯一解D,否则 dimB(K)=1。 通常情况下,f处处不光滑,f的计盒维数大于1。f是仿射映射ωi(i=1,2,…,m)生成的迭代函数系,那么f叫做仿射分形插值函数。 定理2f是迭代函数系{I×R;ωi,i=1,2,…,m}生成的仿射分形插值函数,当且仅当f满足方程 f(Li(x))=Fi(x,f(x)), (5) 其中x∈I,i=1,2,…,m。 定理3假设压缩因子 |si|<1, i=1,2,…,m,两组插值结点集 {(xi,zi):i=0,1,…,m}, f和g是对应的仿射分形插值函数,则 (6) 其中 ‖f-g‖∞=max{|f(x)-g(x)|:x∈I}。 证明令x∈I。假设x∈[xi-1,xi]。根据定理2, 因为 又因为 s=max{|Si|:i=1,2,…,m}<1≤ 同理 因此,记 即 令 G=[a,b]×[c,d] 是R2上的矩形域, {(xi,yj,zi,j):i=0,1,…,m;j=0,1,…,n} 是R3上的一组数集,其中 a=x0 c=y0 令ui(y)(i=0,1,…,m)是 J=[c,d] 上的(m+1)次连续函数,满足插值条件 ui(yj)=zi,j, 其中j=0,1,…,m。 对于任意y∈[a,b]和数集{(xi,ui(y)):i=0,1,…,m},根据上述仿射分形插值函数的构造方法,能得到插值结点集是{(xi,ui(y)):i=0,1,…,m}的仿射分形插值函数gy(x),那么有 gy(xi)=ui(y), i=0,1,2,…,m。 令 f(x,y)=gy(x), (x,y)∈[a,b]×[c,d]。 那么f(x,y)是[a,b]×[c,d]上的一个二元函数,并且满足插值条件 f(xi,yj)=zi,j, 其中i=0,1,2,…,m,j=0,1,2,…,n。 定理4f是G=[a,b]×[c,d]上的一个连续函数。 得到 i=0,1,2,…,m。根据函数f(x,y)的构造方法和定理3,有 令 δ=min{δ1,δ2}, 对于 可以得到 因此函数f(x,y)在G上是连续的。 引理对于任意的x∈[a,b],如果截面z=f(x,y),y∈[c,d]是由迭代函数系 生成的仿射分形插值函数,其中 那么截面 z=f(Li(x),y), y∈[c,d]也是一个由迭代函数系 生成的仿射分形插值函数,其中 证明对于任意的y∈[yj-1,yj],因为截面 z=f(·,y), 都是[a,b]的仿射分形插值函数,据定理2得 f(Li(x),y)=Fi,j(x,f(x,y))= sif(x,y)+ci,yx+di,j, (7) (8) 因为截面 z=f(x,·) 是闭区间[c,d]上的仿射分形插值函数,是由迭代函数系 生成的,那么 又根据方程(7)和(8)得 (9) 因为 z=f(xk,·), i=0,1,2,…,m,是[c,d]上的仿射分形插值函数,根据定理2得 结合方程(9)得 其中Ai,j,Bi,j,Ci,j和Di,j在y上相互是独立的。因此 z=f(Li(x),·) 也是一个仿射分形插值函数。完成引理的证明。 定理5如果ui(y),i=0,1,2,…,m是闭区间[c,d]上的仿射分形插值函数,那么对于任意的x∈[a,b],f(x,·)也是闭区间[c,d]上的仿射分形插值函数。 证明对于任意的固定点x∈[a,b],令 z=g(y) 是闭区间[c,d]上的仿射分形插值函数,插值结点集是 {(yj,f(x,yj)):j=0,1,2,…,n}, 压缩因子是 需要证明对于任意的y∈[c,d], f(x,y)=g(y)。 显而易见,存在连续的{i1,i2,…,ik,…},其中ik∈{1,2,…,m},那么 xk=Li1∘Li2∘…∘Lik(x0)→x,(k→∞)。 因为f(x0,·)是闭区间[c,d]上的仿射分形插值函数,根据引理,截面f(xk,·),k=1,2,3,…是闭区间[c,d]上的仿射分形插值函数,压缩因子是 因为f(·,yj),j=0,1,…,n在闭区间[a,b]上是连续的,对于任意的ε>0,存在N∈Z+,如果k>N,有 |f(xk,yj)-g(yj)|=|f(xk,yj)-f(x,yj)|<ε, j=0,1,…,n,则任意的y∈[c,d]和k>N,根据定理3, |f(xk,y)-g(y)|≤‖f(xk,y)-g‖∞≤ 说明 根据定理4,定理5证明完毕。 [1] BARNSLEY M F. Fractal functions and interpolation[J].Constr Approx,1986(2):303-329. [2] BARNSLEY M F. Fractal everywhere[M].New York: Academic Press,1988:17-18. [3] 江镅,冯志刚.一类多参数分形插值曲面[J].成都信息工程学院学报,2009,24(6):616-618. [4] 戴俊.一例分段连续系统的分形特征[J].江苏科技大学学报:自然科学版,2006,20(5):37-40. [5] 孙秀清.基于分形插值函数生成的分形插值曲面的中心变差[J].镇江高专学报,2014,27(3):44-47. [6] GERONIMO J S,HARDIN D. Fractal interpolation surfaces and a related 2-D multiresolution analysis [J]. Journal of Mathematical Analysis and Application,1993,176 (2) :561-586. [7] DALLA L. Bivariate fractal interpolation functions on grids[J]. Fractals,2002,10 (1):53-58. [8] ROBERT M. The minkowski dimension of the bivartiate fractal interpolation surfaces [J].Chaos Solition and Fractal, 2006(27):1147- 1156. [9] 彭涛.一类具有函数垂直比例因子的分形插值曲面[J].江苏科技大学学报:自然科学版,2010,24(6):615-618. [10] BOUBOULIS P,DALLA L. Fractal interpolation surfaces derived from fractal interpolation functions[J]. Math Anal Appl,2007 (336):919-936. 〔责任编辑: 卢 蕊〕 Aconstructionmethodofaclassoffractalinterpolationsurfaces SUNXiu-qing (Basic Courses Department,Zhenjiang Branch of Jiangsu Joint Vocational and Technical College, Zhenjiang 212016,China) A construction method of fractal interpolation surface on a rectangular domain with arbitrary interpolation nodes is introduced. The continuity of the bivariate functions corresponding to this type of fractal interpolation surfaces is proved. affine fractal interpolation function; vertical scaling factors; fractal interpolation surface 2014-12-05 国家自然基金会资助项目(51079064) 孙秀清(1978—),女,吉林松原人,讲师,硕士,主要从事数学分形插值函数研究。 O186.1 : A :1008-8148(2015)02-0055-04
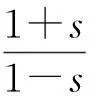

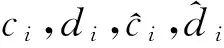
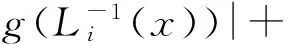
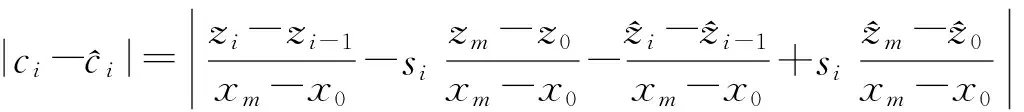








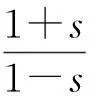
2 构造分形插值曲面