大型回转窑筒体结构的力学行为思考

杨爱龙

（中材装备集团有限公司，天津 300400）

大型回转窑筒体结构的力学行为思考

杨爱龙

（中材装备集团有限公司，天津 300400）

本文通过建立含耐火砖模型和函数加载有限元模型对大型回转窑筒体变形和应力的计算结果进行了详细分析。

大型回转窑 筒体结构 力学行为

1. 回转窑的支撑与摩擦载荷分析

由于筒体的长度要比其直径大得多，因此可以采用超静定变刚度连续梁模型来对筒体各档支承的支撑载荷进行计算。筒体的总长是50.95 m,内半径1.375 m，且各处的厚度不同。在不考虑下滑静摩擦的影响我们可以将筒体视为水平连续梁处理后的等效重力加速度为g′=9.8cos 2.977°=9.787 N kg。而筒体的材料是Q345C，其密度ρ=7.85×103kg m3，筒体的总质量是127 426.0 kg。筒体内部耐火砖层的质量是199 030.7 kg，物料质量是11 000.0 kg，他们在回转窑内以螺旋式向前移动，其速度比较均匀，物料质量在轴线方向被视为均布载荷。因此可以将物料、耐火砖和筒体的自重合在一起视为作用于水平梁的等效均布载荷,其集度q= (337 456.7×9.787) /50.95=64.822 kN/ m。

窑尾扬料板和密封物的质量是1 705.15 k，集中力载荷F1=16.688 kN。由于筒体上和切向钢板连接的范围相对较小，所以也可以将大齿轮的质量看做集中力载荷，为F2=51.614 kN。然后就可以用Ansys软件计算超静定变刚度连续梁的支反力。

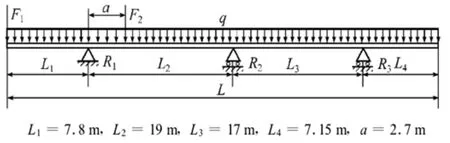
如上图所示，建立模型，并分段定义梁单元的几何参数，得出下图中的超静定变刚度连续梁有限元模型。

其应力和挠度都不能对筒体的局部变形和应力状态进行准确的反映，建立这个模型的作用主要是计算得到各档支承的竖直方向支反力，分别为R1=1 201.460 3 kN、R2=1 159.928 5 kN、R3=1 009.594 kN。

2. 筒体变形和应力的计算结果分析

2.1 静止工况下筒体的变形和应力状态

本文采用采用含耐火砖模型和函数加载模型对实际稳定运转工况下的回转窑进行了计算，并通过对筒体横截面圆度的分析，试图找出筒体强度和刚度上的薄弱点。

2.1.1 变形状态分析

在利用含耐火砖有限元模型去计算在静止工况下的回转窑，可以得其轮带的变形情况。变形情况等比例放大之后，可以看出变形量很小，最大的时候才达到1.109 mm。最大的变形发生在Ⅰ、Ⅱ挡支承之间的靠近中央位置的筒体正下方的外壁上，而第Ⅰ、Ⅱ档支承之间筒体跨距是19m，第Ⅱ、Ⅲ档之间跨距是17m，造成这一现象的原因可以用材料力学连续梁理论解释，即超静定多跨连续梁的最大挠度总是发生在最长跨距段的近似中央位置。

2.1.2 应力状态分析

经过比较和验证，可得出在各档轮带的托轮支撑接触区存在应力集中，且最高达到101.3 MPa，最高点出现在第一档轮带的支撑接触区，但并没有触及轮带材料的屈服极限。

2.2 稳定运转工况下筒体的变形和应力状态

分析筒体在稳定运转工况下的变形与应力状态，只需要在静止模型中采用含耐火砖有限元模型，并增加转矩和摩擦载荷。

2.2.1 变形状态分析

下图所示的是通过计算得出的是在稳定运转工况下筒体和轮带的总体变形情况。从图中可以看出筒体受大齿轮转矩作用发生变形，最大变形为1.109 mm，发生位置和静止状态相比，沿转矩环向偏转大约9°。

2.2.2 应力状态分析

本文的关注重点在于在稳定运转工况下的筒体部分的应力强度，下图(a)所示的是在单独抽取和观察的筒体的应力场的当量应力分布情况，其中最大的当量应力发生在筒体中间档轮带支承位置的内表面，最大值是20.625 MPa。而且筒体大部分区域的当量应力分布呈现出纵向对称性，而且具有较高的安全系数，但是应力在轴向分布上很不均匀，在三档支承节段上的应力是悬空筒节段上应力的3到4倍。若果筒体发生支承磨损与偏斜或者筒体的物料载荷增加，那么档位支承段筒体的应力状态就会被严重破坏，因此十分有必要对档位支承段筒体的厚度进行补强和优化。

而大齿圈处的局部筒体的应力集中，但是其最高应力值也比较小，因此具有较高的安全性。由此可见，在实际运转工况下的筒体的应力要比停工静止状态下的应力大，但是变化相对较小，表明大齿轮的托轮支承和回转转矩之间的摩擦阻力对筒体应力分布的影响是微小的，因此，将回转窑窑体结构处理为静止状态进行工程分析也是准确的。

2.3 稳定运转工况下筒体函数加载有限元模型的比较分析

采用函数加载有限元模型对稳定运转工况下的筒体当量应力进行计算，如下图所示，其中筒体的最大当量应力发生在筒体与中间轮带支承位置的接触区，最大值是24.162 MPa，这一计算结果与前文所提到的用含耐火砖有限元模型进行计算的结果相比，得出的最高应力结果较大，但是两者的应力分布规律相一致。含耐火砖模型单元数为59 737,总自由度数为614 150，而函数加载模型的单元数为42 641,总自由度数为458 392，因此，在总自由度上函数加载模型相较较少了大约1/4，从而使计算效率有所提高。

2.4 稳定运转工况下筒体的横截面圆度分析

筒体的横截面圆度对于回转窑的安全运转来说具有十分重要的意义，如果筒体的横截面圆度很差的话，将很容易导致振动或者耐火砖的掉碎砖现象，使筒体壁产生局部高温，导致疲劳破损、材料劣化，将对筒体的强度安全造成威胁。

横截面在X方向的最大正位移UXmax和最小位移UXmin恰好在左右两个端点，Y方向的最大正位移UYmax和最小位移UYmin恰好在上下两个端点。选取图中的对应点课读出位移的数值，分别是UXmax=0.351 22、UXmin=-0.347 36、UYmax= -0.007 663、UYmin=-0.662 80，通过计算可以得出横截面的圆度是0.676 86mm。在以同种方法推算出截面A、C、D的圆度分别为cA=0.653 88 mm,cC=0.509 93 mm,cD=0.033 707 mm。比较可得横截面B的圆度最大，也就是说在第二档轮带附近筒体的圆度是最差的，从而得出在中间轮带支承附近的筒体内部掉碎砖现象最为严重，因此在日常对筒体进行检修时，需要重点关注支承区域筒体内部是否发生掉碎砖现象，并且对注重对筒体厚度的优化，对截面刚度的补强。

小结：本文通过建立含耐火砖模型和函数加载有限元模型对大型回转窑筒体变形和应力的计算结果进行了详细分析。可以得出以下结论，第一，回转窑在静止和运转两种工况下的表型情况和应力都可以满意相应的刚度和强度条件。第二，实际运转时筒体最高应力发生在筒体与中间档轮带接触区的内表面。第三，中间档轮带附近的筒体圆度最差，最容易出现问题。第四，各档位段的支承载荷分配不均，以至于筒体的应力分布不均匀。

[1]王和慧,陈一凡,谢可迪,王东良,王守波,朱斌,周金水. 回转窑液压挡轮的应力强度与疲劳断裂分析[J]. 机械强度. 2009(06)

[2]唐鼎,刘义伦,赵先琼. 大型回转窑筒体力学状态综合分析[J]. 水泥. 2013(01)

[3]王峰圃,李强,姜奎松. 回转窑筒体裂纹产生原因分析及修复[J]. 机械研究与应用. 2010(01)

TQ172

B

1007-6344（2015）11-0003-01