利用频率指纹检测耐火砖的内部损伤
孟 浩,王志刚,刘昌明
(武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉 430081)
1 引言
耐火砖在生产过程中容易产生断层、裂纹等内部损伤[1],损伤严重时会极大降低耐火砖的使用性能。若将性能低劣的耐火砖投入使用,可能会造成严重的安全事故。因此,对耐火砖进行损伤识别具有重大意义。目前的耐火砖损伤检测技术应用较多的有超声波检测法,声发射检测法,冲击回波检测法[2],这些方法虽然检测精度高,但操作复杂,成本较高,无法满足批量检测的要求。因此,寻求一种高效率、低成本、易操作的耐火砖损伤检测方法迫在眉睫。
频率不仅可以反映结构的健康状况,而且是结构动力学响应中最易测得且测量最准的特征量。利用频率指纹进行损伤检测具有高效性、准确性和经济性等优点,因此频率指纹被广泛应用于桥梁、混凝土、木材、农作物等方面的损伤检测中[3],在耐火砖的损伤检测领域也已有相关应用:文献[4]建立了一套耐火砖内部质量检测系统,通过分析敲击声信号的一阶固有频率,可以自动识别受损的耐火砖;文献[5]利用模糊聚类的方法分析耐火砖的共振频率,识别了受损耐火砖并确定了其损伤类型。
但上述方法仅判断了耐火砖是否受损,而没有进一步的损伤定位或损伤定量的研究。耐火砖的模态频率不仅与损伤程度有关,还受损伤位置的影响。文献[6]在对结构进行模态分析时得出结论:任意两阶频率变化量之比仅是损伤位置的函数而与损伤程度无关。文献[7]提出任意两阶模态频率变化量的平方比仅是结构损伤位置的函数。故只有确定了耐火砖的损伤位置,才能进一步确定其损伤程度。国内外利用模态频率进行损伤定位的研究众多。文献[8]提出了利用频率变化量之比和模态应变能变化率进行梁类结构的损伤识别:先根据频率变化量之比确定损伤的可疑位置;再通过损伤前后模态应变能的变化率准确定位损伤位置。文献[9]利用频率变化量的平方比作为损伤的动力指纹,判定结构的损伤位置,并采用插值法从频率改变率中获取刚度损失量进行损伤定量。
根据结构的动力学响应特性可知,高阶模态频率的能占比较低,实际测试中高阶模态频率不易测得。通过实验可较好测得耐火砖的前三阶模态频率,根据耐火砖损伤后第三阶与第一阶频率变化量的比值以及第三阶与第二阶频率变化量的比值确定耐火砖的损伤位置,并根据该位置频率变化率与损伤系数的关系曲线图,确定耐火砖的损伤程度。
2 损伤位置的确定
2.1 理论分析
任意结构的振动特性都可以看作是由质量、阻尼以及刚度矩阵构成的振动系统。若忽略阻尼的影响,结构的振动方程为:

式中:K—结构刚度矩阵;M—结构质量矩阵;ω—固有频率;φ—振型。
发生损伤后,结构的质量和刚度会改变,从而结构的固有频率和振型也会发生改变,由摄动理论式(1)可知:

式中:ΔK—刚度矩阵变化量;ΔM—质量矩阵变化量;Δω—频率变化量;Δφ—振型变化量。耐火砖的内部缺陷导致结构刚度明显降低,而质量变化并不明显。若不考虑质量变化,则ΔM=0;式(2)则变为:
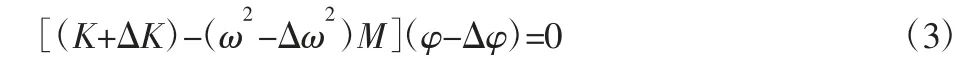
展开式(3),且忽略二阶项,整理可得:

单元变形可以由结构振型推导出来,对于某阶模态i(i=1,2,3…)则有:

式中:A—结构单元总数;m—单元号;ε—单元变形。若结构只存在单个损伤,即损伤单元只有一个,设损伤单元为N,则:

由式(6)可以看出,在不同阶数的模态频率下,单元的变形是变化的,而单元的刚度矩阵变化量ΔK 是不变的,因此定义单元损伤系数[9]:

式中:αN—损伤系数矩阵;KN—单元损伤前的刚度—单元损伤后的刚度,则:

将式(8)带入式(6)得:

同理,对于某阶模态j(j=1,2,3…)有:

两式相比得到损伤后任意两阶频率变化量之比:

由式(11)可知,结构损伤后任意两阶频率变化量的比值仅与损伤位置有关,与损伤程度无关。
2.2 数值仿真
选取的耐火砖主要参数为:弹性模量E=21542MPa,泊松比σ=-0.53,密度 ρ=2162kg·m-3,b×h×l=115mm×60mm×230mm。耐火砖的形状是对称的,若采用对称的约束形式,会推导出两个损伤位置,因此将耐火砖以悬臂梁的形式进行约束。分别在耐火砖的10mm、20mm、30mm…220mm 处(0mm 处为耐火砖的自由端)制造深15mm、宽0.8mm 的贯穿性缺口模拟损伤,利用有限元数值仿真软件对耐火砖进行模态分析,得到不同损伤位置Δω3与Δω1、Δω3与Δω2的比值。以耐火砖的损伤位置为横坐标(横坐标为归一化坐标,耐火砖的自由端为横坐标的零点),以Δω3与Δω1的比值为纵坐标绘制曲线图,如图1 所示。
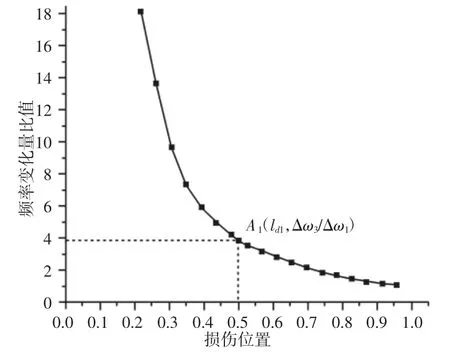
图1 Δω3/Δω1 随损伤位置变化的曲线图Fig.1 Curve Map of Δω3/Δω1 with Position Change
同样,以耐火砖的损伤位置为横坐标,以Δω3与Δω2的比值为纵坐标绘制曲线图,如图2 所示。

图2 Δω3/Δω2 随损伤位置变化的曲线图Fig.2 Curve Map of Δω3/Δω2 with Position Change
通过实验测得结构完好时前三阶频率ω1、ω2、ω3的值,以及结构损伤后前三阶频率的值。算出 Δω3/Δω1的值,在图1 中作一条过点(0,Δω3/Δω1)的水平线,与曲线交于点 A1(ld1,Δω3/Δω1),该点的横坐标 ld1即为损伤位置。或算出 Δω3/Δω2的值,在图 2 中作一条过点(0,Δω3/Δω2)的水平线,与曲线交于点A2(ld2,Δω3/Δω2),该点的横坐标 ld2即为损伤位置。经仿真和实验发现,当损伤位于耐火砖(0~50)mm 位置时,无法准确推导出损伤的位置,由于耐火砖结构的对称性,只需置换耐火砖的约束端与自由端,损伤位置则变换到(180~230)mm 位置之间,从而确定损伤位置。
3 损伤程度的确定
文献[10]在利用共振频率测试耐火砖弹性模量的研究中,推导了耐火砖的一阶共振频率ω、截面惯性矩J 以及弹性模量E 之间的关系:

耐火砖的截面惯性矩J=bh3/12,某处受损后,损伤处横截面的高hd=h-h0,截面惯性矩耐火砖某处存在损伤时,此处的截面惯性矩减小,进而导致结构整体的截面惯性矩减小。随着损伤程度的加剧,结构的整体截面惯性矩J 会随之减小,结合式(12)可知,由于弹性模量E 为定值,频率ω 也会随之降低。
沿x 轴方向将耐火砖平均划分成23 个单元,如图3 所示。其中耐火砖的右端为自由端。
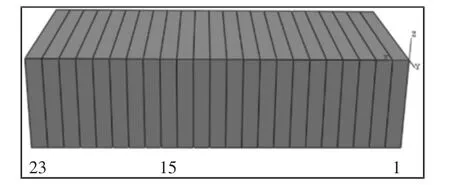
图3 单元划分图Fig.3 Unit Division
在第一个单元的中间位置制造宽为0.8 mm、深为h0的贯穿性缺口模拟损伤,通过有限元数值仿真软件对耐火砖的损伤进行分析,计算出未受损时耐火砖的一阶模态频率ω1以及不同损伤深度时耐火砖的一阶模态频率引用损伤系数α=h0/h 描述损伤程度,以损伤系数α 为横坐标,频率变化率为纵坐标,根据分析结果绘制出单元1 的频率变化率与损伤系数的关系曲线图。利用相同的方法分别绘制出第2-23 个单元频率变化率与损伤系数的关系曲线图,曲线图的变化趋势基本相同,其中单元15((150~160)mm 位置)的频率变化率与损伤系数的关系曲线图,如图4 所示。

图4 单元15 的频率变化率-损伤系数变化曲图Fig.4 Curve of Frequency Variation with Damage at Fifteenth Units
4 实验验证
在耐火砖的155 mm 处(位于第15 个单元),制造一个宽0.8 mm、深20 mm 的贯穿性缺口,使用敲击锤敲击耐火砖,接收并存储敲击产生的声信号。利用MATLAB 软件对声信号进行FFT 变换,提取耐火砖的前三阶模态频率。分析结果,如表1 所示。

表1 分析结果Tab.1 Analysis Results
在图1 中作一条过点(0,2.33)的水平线,与曲线交于点A1,如图5 所示。在图2 中作一条过点(0,3.75)的水平线,与曲线交于点A2,如图6 所示。由图5 可知A1的横坐标在0.67 附近,对应的耐火砖损伤位置ld1为154.1 mm。由图6 可知A2的横坐标在0.66 附近,对应的耐火砖损伤位置ld2为151.8 mm。根据ld1和ld2可以确定损伤位于第15 个单元。在图 4 中作一条过点(0,14.5)的水平线,交曲线于点D,如图7 所示。点D 对应的横坐标误差为故此方法可以较为准确的推断耐火砖的损伤位置和损伤程度。

图5 Δω3/Δω1 随损伤位置变化的曲线图Fig.5 Curve Map of Δω3/Δω1 with Position Change

图6 Δω3/Δω2 随损伤位置变化的曲线图Fig.6 Curve Map of Δω3/Δω2 with Position Change

图7 单元15 的频率变化率-损伤系数变化曲线图Fig.7 Curve of Frequency Variation with Damage at Fifteenth Units
5 结论
首先从理论上推导了损伤导致的任意两阶频率变化量之比仅是损伤位置的函数而与损伤程度无关,依此绘制出耐火砖频率变化量的比值与损伤位置的关系曲线图,根据频率变化量的比值确定了耐火砖的损伤位置;再绘制出该位置第一阶频率变化率与损伤系数的关系曲线图,通过频率变化率确定了耐火砖的损伤程度。并和实验结果做了对比,结果表明:(1)通过耐火砖损伤后的第一阶与第二阶频率变化量的比值可以确定损伤位置。(2)确定损伤位置后,根据该位置第一阶频率变化率与损伤系数的关系曲线图可以确定损伤程度;(3)对位于耐火砖(0~50)mm 位置的损伤,直接采用该方法不能获取损伤位置,须置换耐火砖的约束端与自由端,此时损伤位于耐火砖(180~230)mm 位置,即可确定损伤位置。

