带冲突关系装箱问题的启发式求解算法

元 野， 李一军

(1.哈尔滨工业大学 管理学院，哈尔滨 150001； 2. 国家自然科学基金委员会 管理科学部，北京 100085)



带冲突关系装箱问题的启发式求解算法

元 野1， 李一军2

(1.哈尔滨工业大学 管理学院，哈尔滨 150001； 2. 国家自然科学基金委员会 管理科学部，北京 100085)

现实物流活动中大量存在的食品、药品和危险品等货物的分组包装问题属于带冲突关系的装箱问题(BPPC)，其优化目标是在满足货物间冲突限制的前提下完成装箱操作，并最小化使用货箱的数量。本文从实际需求出发，基于货物之间的冲突关系、装箱顺序和货箱容量等约束建立相应的数学规划模型；随后设计了求解BPPC问题的启发式算法，算法通过迭代求解最大团结构实现货物间冲突关系的消去，根据当前货物最大团采用改进降序首次适应算法(FFD)完成货物装箱操作，并通过“洗牌”策略对已有装箱方案进行局部优化；最后，针对Iori算例数据，将以上算法与基于图着色的启发式算法进行比较分析，结果表明，本文算法是求解BPPC问题更为有效的方法。

运筹学与控制论；冲突装箱问题；最大团；启发式算法

0 引言

装箱问题(bin packing problem, BPP)是一个经典的组合优化难题，在切割加工与物流运输等领域有着广泛应用，并已被证明属于NP完全问题[1,2]。在对食品、药品以及某些危险品货物的包装过程中，由于不同的物理、化学或生物性质，导致某些货物不允许被装入到同一个货箱当中，由此便产生了带有冲突关系的装箱问题(bin packing problem with conflicts, BPPC)。BPPC模型是在经典装箱模型的基础上，加入了货物冲突限制，是装箱模型与图着色模型的结合形式，求解时需要兼顾“密集装箱”与“冲突化解”两方面的内容，才能实现问题的全局优化[3]。

BPPC模型源于经典装箱问题模型，但其求解难度更大，目前国内外针对这一问题的研究内容甚少。Jansen[4]首次将BPPC模型中的冲突关系表示成图结构形式，通过迭代的求解最大导出子图，设计了渐近式近似求解算法框架；Gendreau等[5]首次提出了BPPC问题的整数规划模型，并分别从装箱模型和图着色模型两个角度探讨了问题下界；Muritiba等[6]采用集合覆盖的方式对BPPC问题进行了重新建模，在对问题下界进行近似讨论的基础上，提出了分支定界算法进行精确求解；Khanafer等[7]基于树结构分解的方式设计了求解BPPC问题的通用算法框架；Elhedhli等[8]通过定义分支规则来消除冲突约束，基于此采用动态规划的方式进行计算。从模型求解角度，作为NP-hard问题，传统数学规划方法和精确算法在求解能力和效率上有所不足，针对BPPC模型的特征，需要设计包含冲突化解和货物装箱的两阶段启发式算法。冲突关系的定义和消去可以基于冲突图结构来实现，其思想源于图着色模型中的最小色数问题[9,10]；而装箱问题的启发式算法在文献[11]当中进行了系统总结。此外，BPPC模型及其求解算法还可以应用于特定的调度问题和资源分配问题，例如排考问题的建模和求解[12]。

本文重点阐述BPPC问题的数学模型，并基于该模型设计包含冲突化解和货物装箱过程的求解算法。主要包括三方面的工作：首先，引入冲突图结构来对货物之间的冲突关系进行描述，将货物集合定义为图结构上的冲突因子；其次，针对图着色过程中货物划分易陷入局部最优的缺点，从冲突图的补图——兼容图入手，迭代求解其最大团结构，获取当前相互之间不存在冲突关系的最大货物子集；第三，基于数学模型和当前获取的最大团结构，采用改进降序首次适应启发式求解算法实现装箱操作。最后选取国际标准算例进行仿真验证，实验结果表明，上述算法是求解BPPC模型的有效方法。

1 BPPC问题的数学规划模型

BPPC模型的基本定义可以描述为：给定由n件重量分别为w1,w2,…,wn的货物组成的货物列表I和由m个最大容量均为c的货箱组成的货箱列表H；I中的任意一件货物i对应一个冲突货物列表Li，其中的每件货物均与i之间存在冲突关系，即不允许与i装入到同一货箱当中；模型的求解目标是在满足货箱容量和货物间冲突约束的前提下，将I中的所有货物装入货箱当中，并最小化所使用货箱的数量[5]。为具体描述货物之间的冲突关系，引入冲突图的定义如下。

定义1 冲突图CG=(CV,CE)为一个无向图，代表I内所有货物之间的冲突关系。其中，顶点集合CV对应I中的每件货物，边集CE对应货物之间的冲突关系。

为方便冲突关系消去和后续装箱操作，需要对冲突图中的边集CE进行如下扩展：首先，对任意货物i∈I，在i与其对应的冲突货物列表Li内的每件货物之间添加一条边；其次，对任意两件货物i,j∈I，如果wi+wj>c，则在i和j之间添加一条边。

BPPC数学模型需要用到的决策变量包括：

数学规划模型表示如下[7]：

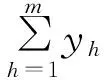
(1)

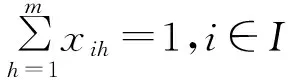
(2)

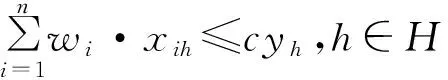
(3)

xih+xjh≤yh,(i,j)∈CE,h∈H

(4)

yh∈{0,1},h∈H

(5)

xih∈{0,1},i∈I,h∈H

(6)

以上模型当中，(1)式表示BPPC模型的目标函数；(2)式表示任意一件货物只能装入到一个货箱当中；(3)式表示任意一个货箱中装入所有货物的重量之和不允许超过货箱的最大容量；(4)～(6)式表明任意一个货箱当中装入的所有货物都必需满足冲突约束限制。

2 基于最大团的BPPC问题启发式算法

BPPC模型较为直观的解法是基于冲突图结构上的独立集来消去冲突关系，通常采用图着色的方式实现，即对冲突图CG中可以装入到同一货箱中的货物着以相同的颜色，求得货物列表I的一个划分，并基于每一划分进行装箱。然而，图着色过程不仅时间复杂度较高，并且由于强制将货物列表I进行划分，容易陷入局部最优的状态，很难取得质量很高的装箱方案。针对这一缺陷，本文将冲突图的补图定义为兼容图，迭代求解兼容图上的最大团结构，每次根据当前获取的最大团采用改进降序首次适应的方法进行装箱操作，并通过“洗牌”策略对获取的装箱方案进行局部再优化，以期获取质量更高的装箱方案。

2.1 基于最大团结构的冲突关系消去方法

2.1.1 最大团的定义

定义2[13]给定简单无向图G=(V,E)，其中的完全子图Q称为图G中的一个团结构，即Q中任意两个顶点之间都有E中的一条边相连接，如图1所示。

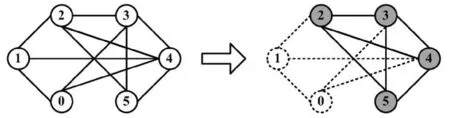
图1 团结构示意图

定义3 对于给定图G中的一个团结构Q和顶点υ(v∈G且υQ)，如果顶点集合Q∪{υ}仍为图G中的一个团结构，则记υ为团Q的邻接顶点，且将Q在G中的所有邻接顶点数目记为ρ(Q)。

定义4[13]对于图G中的团结构Q来说，如果ρ(Q)=0，则称Q为图G的一个极大团；顶点数量最多的极大团称为图G的最大团。

显然，图G的最大团一定是它的极大团，反之不成立。最大团问题(maximum clique problem, MCP)的求解也是NP难的，随着图中顶点数量的增多和边密度的增大，求解问题的时间复杂度越来越高。因此，通常采用启发式算法或智能算法进行求解。

2.1.2 基于最大团的冲突消去总体策略

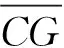
兼容图是冲突图的转换形式，冲突图上的独立集等价于兼容图上的团结构，都对应不含冲突关系的货物子集。因此，求解冲突图上的独立集和兼容图上的团结构是两种消去货物间冲突关系的有效方法，二者基于不同的数据结构得以实现。根据BPPC模型定义，冲突消去的目的是在货物列表I中寻找可相互兼容的货物子集I’，并基于I’进行装箱操作。本文通过求解兼容图上的最大团结构来搜索可相互兼容的货物子集，设计了基于最大团结构的冲突消去方法，其具体步骤如下[5]：

Step 1 从还未装箱的货物列表当中挑选出与所有货物间均不存在冲突关系的货物集合，即从冲突图CG=(CV,CE)中挑选出所有度数为零的顶点集合CV0，并令冲突图CG=(CV-CV0,CE)；若CV=∅，则转至Step 4；

Step 2 采用2.1.3小节部分中介绍启发式策略计算当前冲突图CG=(CV-CV0,CE)中的一个最大团D，并随机选取货物i∈D；

Step 4 令DI=Di∪CV0，DI则为货物列表的一个冲突消去结果；

Step 5 输出DI，当前冲突消去过程结束。

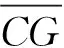
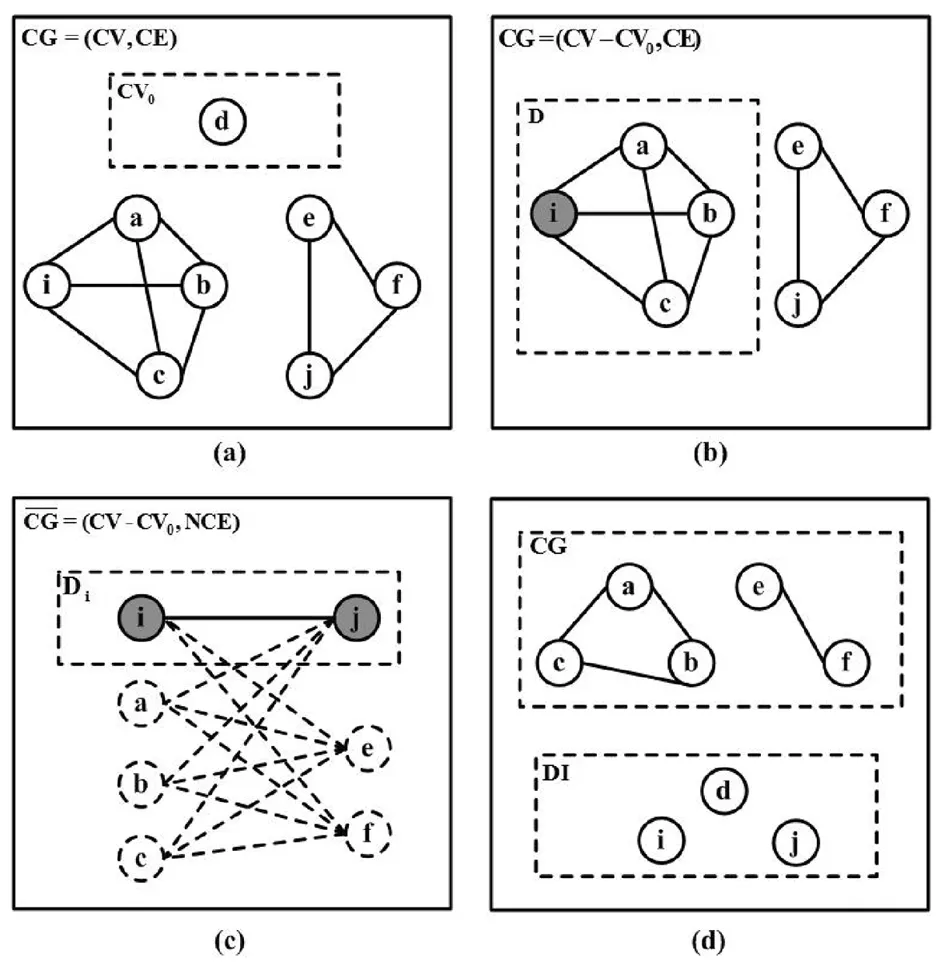
图2 冲突消去过程示例

2.1.3 最大团的计算

冲突消去过程中，针对冲突图和兼容图的最大团计算是核心内容，并且后续的装箱操作也是基于当前兼容图上的货物最大团进行。因此，最大团的求解质量决定了可同时执行装箱操作的货物规模，是获得较优装箱方案的基础。此外，目前计算最大团的启发式算法通常是基于当前已获得的极大团列表，从中挑选出顶点数最多的一个极大团作为结果输出，因此，算法还需要充分考虑给定图结构上极大团的搜索能力[14]。综合以上分析内容，本文基于给定图结构的邻接矩阵和当前最大团，采用顶点插入过程和顶点取代过程进行优化，设计了迭代求解最大团的启发式搜索算法。

(1)顶点插入过程

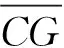
(2)顶点取代过程

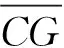
(3)启发式搜索策略

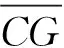
Step 2 基于极大团Qi，调用顶点插入过程对Qi进行扩展；

Step 3 基于扩展后的极大团Qi，遍历其中全部可取代的顶点，调用顶点取代过程对Qi进行再扩充，并从顶点取代结果中选取顶点数最多的Qi插入到极大团列表List中；

Step 4 若不存在还未遍历的顶点i，则选取顶点数最多的Qi，令Qmax=Qi，并转至Step5；否则令i=i+1，并转至Step 1；

Step 5 从List中随机选取两个极大团Qx和Qy，令Qx,y=Qx∩Qy，并依次调用顶点插入过程和顶点取代过程对Qx,y进行扩展；

Step 6 若Qx,y中顶点数量多于Qmax，则令Qmax=Qx,y；否则，若不满足算法终止条件(执行Step 5的最大次数，此处设定为100次)，转至Step 5；

Step 7 输出Qmax，一个最大团的计算过程结束。

2.2 改进FFD启发式装箱算法

经过冲突关系消去后得到的货物最大团即为当前可直接进行装箱操作的货物集合。通常来说，为了获取质量较高的装箱方案，需要基于“大件货物优先装箱”和“密集装箱”两项原则进行方案构建。其中，“大件货物优先装箱”原则是指优先考虑将重量较大的货物装入到货箱当中；“密集装箱”原则是指针对某一个已被使用的货箱来说，尽可能向其中装入更多的货物。以上两个原则的实质是提高每个货箱的空间利用率，即一个货箱中已装入的所有货物重量之和与该货箱最大容量之间的比值。算法可以通过提高所有货箱的空间利用率来减少装箱方案中所使用货箱的数量。因此，针对一个不含冲突关系的货物集合，本文基于著名的降序首次适应算法[16](First Fit Decreasing, FFD)进行改进，设计了一种包含构建过程和优化过程的启发式装箱算法。

在初始状态下，问题的启发式信息只有各货物的重量和货箱的容量值，因此，需要依据“大件货物优先装箱”原则构建一个较优的初始装箱方案。具体过程为：首先，按照货物列表中货物重量由大到小的顺序对货物进行重新排序；然后，顺次遍历排序后的货物列表，如果当前货箱的剩余容量可以容纳遍历到的货物，则对该货物进行装箱操作，并将其从货物列表中删除；否则，跳过该货物继续遍历余下货物；最后，如果遍历完成后，货物列表仍不为空，则开启一个新货箱，重复以上装箱过程，直到所有货物均完成装箱操作为止。

通过以上操作得到一个完整的装箱方案之后，问题的启发式信息变为各货箱的空间利用率，因此，需要依据“密集装箱”原则提高货箱空间的利用情况，从而进一步减少使用货箱的数量。具体过程为：首先，从已有装箱方案中选取空间利用率最低的一个货箱，复制保存其中的所有货物信息，并释放该货箱空间；其次，采用“洗牌”策略[2]对上述货物进行重新装箱，即顺次遍历每件货物，依据现有各货箱的剩余容量，采用首次适应算法[16](First Fit, FF)执行装箱操作。如果通过“洗牌”策略得到更优的装箱方案，则用新方案取代旧方案，否则继续重复执行上述操作，直到满足算法终止条件为止(由于“洗牌”操作中不包含随机过程，此处的算法终止条件为连续执行10次“洗牌”操作仍无法得到有所改进的装箱方案)。

图3 算法流程图

2.3 算法总体流程

以上内容详细介绍了针对BPPC模型的冲突消去过程和货物装箱过程。冲突消去过程主要通过最大团结构的表示和求解来实现，货物装箱过程主要通过改进FFD算法来实现，二者有序结合在基于迭代过程的算法框架当中。流程图如图3所示。

3 实验与分析

为验证算法性能，选取文献[6]中基于标准装箱问题算例设计的实验数据进行测试，所有实验数据可以从网站http://www.or.deis.unibo.it/research_pages/ORinstances/BPPC.html上下载。算例分为三类，货物数量分别为120、250和500，其中每件货物的重量在20～100之间随机选定，所有货箱容量值固定为150。每一类算例按照冲突货物数量的密度值δ(0.1≤δ≤0.9)不同进一步划分为九个小组，每个小组有十个具体算例。密度值δ的计算方式为：对某一货物i赋予一个满足[0,1]区间上均匀分布的特征值pi，那么，对于同组算例中的另外一件货物j，如果满足(pi+pj)/2≤δ，则在货物i与货物j之间添加一对冲突关系。为验证提出算法的有效性，选取文献[17]中提出的基于图着色的冲突消去方法与本文提出的基于最大团的冲突消去方法分别实现并进行比较，比较内容主要包括针对每组算例计算得出的最优值、最差值和均值，并通过均值来计算算法改进效率。所有算法细节采用Java语言来实现，相应的虚拟机版本为Java Development Kit 1.7.0，具体计算结果如表1所示。

表1 两类启发式算法计算结果对照表

(1)在货物数量规模相同的一类算例内部，当冲突密度值较小的时候(0.1≤δ≤0.3)，由于兼容图中的边较为稠密，算法求解质量主要取决于改进FFD装箱算法的性能，此时本文提出算法相比基于图着色过程的启发式算法改进程度较小；随着冲突密度值的增大(0.4≤δ≤0.6)，兼容图中的顶点集合划分数量增多，此时基于最大团的启发式算法更为有效地将冲突消去过程和装箱过程有机结合在一起，计算结果的改进程度较大；在冲突密度值最大的情况下(0.7≤δ≤0.9)，兼容图中的边较为稀疏，算法求解质量与冲突消去过程密切相关，此时本文提出算法具有更强的兼容货物搜索能力，但计算结果的改进能力有所下降。

(2)从整体角度来看，不同规模的三类算例在计算结果上均有所改进。相比基于图着色过程的启发式算法，本文提出算法通过迭代方式搜索兼容图上的货物最大团，更大限度的发挥改进FFD装箱算法的计算性能，有助于获得质量更优的装箱方案。

4 结论

带冲突关系装箱问题是图着色问题与装箱问题这两个经典NP难题融合之后的一个新问题。尽管该问题在实际物流系统中的应用更为广泛，但由于问题的复杂性，直至最近几年才引起国内外学者们的关注。本文根据问题的数学模型，采用最大团计算取代图着色方式实现货物冲突关系的消去，并基于此设计了求解该问题的一个混合启发式算法。实验表明，本文提出的算法有效地将“冲突化解”和“货物装箱”过程融为一体，根据问题蕴含的启发式知识引入局部搜索算子，在保证求解质量的同时，确保了算法的稳定性。但通过实验也发现，算法有时也容易陷入局部最优，尤其问题规模较大时，其求解质量会受到影响，下阶段工作将侧重解决这一方面的问题。

[1] Wäscher G, Haußner H, Schumann H. An improved typology of cutting and packing problems[J]. European Journal of Operational Research, 2007, 183(3): 1109-1130.

[2] Zhu W B, Zhang Z Y, Oon W C, Lim A. Space defragmentation for packing problems[J]. European Journal of Operational Research, 2012, 222(3): 452- 462.

[3] Lin Y H, Lin C, Lin B. On conflict and cooperation in a two-echelon inventory model for deteriorating items[J]. Computers & Industrial Engineering, 2010, 59(4): 703-711.

[4] Jansen K. An approximation scheme for bin packing with conflicts[J]. Journal of Combinational Optimization, 1999, 3(4): 363-377.

[5] Gendreau M, Laporte G, Semet F. Heuristics and lower bounds for the bin packing problem with conflicts[J]. Computers & Operations Research, 2004, 31(3): 347-358.

[6] Muritiba A E F, Iori M, Malaguti E, Toth P. Algorithms for the bin packing problem with conflicts[J]. INFORMS Journal on Computing, 2010, 22(3): 401- 415.

[7] Khanafer A, Clautiaux F, Talbi E. New lower bounds for bin packing problems with conflicts[J]. European Journal of Operational Research, 2010, 206(2): 281-288.

[8] Elhedhli S, Li L Z, Gzara M, Naoum-sawaya J. A branch-and-price algorithm for the bin packing problem with conflicts[J]. INFORMS Journal on Computing, 2011, 22(3): 404- 415.

[9] Galinier P, Hertz A. A survey of local search methods for graph coloring[J]. Computers & Operations Research, 2006, 33(9): 2547-2562.

[10] Balogh J, Butterfield J. Excluding induced subgraphs: critical graphs[J]. Random Structures & Algorithms, 2011, 38(1-2): 100-120.

[11] Balogh J, Békési J, Galambos G. New lower bounds for certain classes for bin packing algorithms[J]. Theoretical Computer Science, 2012, 440-441: 1-13.

[12] Gogos C, Alefragis P, Housos E. An improved multi-staged algorithmic process for the solution of the examination timetabling problem[J]. Annals of Operations Research, 2012, 194(1): 203-221.

[13] 潘全,郭鸣,林鹏.基于MapReduce的最大团算法[J].系统工程理论与实践,2011,31(S2):150-153.

[14] Chen Q, Fadlullah Z M, Lin X D, Kato N. A clique-based secure admission control scheme for mobile adhoc networks(MANETs)[J]. Journal of Network and Computer Applications, 2011, 34(6): 1827-1835.

[15] Dang D C, Moukrim A. Subgraph extraction and metaheuristics for the maximum clique problem[J]. Journal of Heuristics, 2012, 18(5): 767-794.

[16] Elhedhli S. Ranking lower bounds for the bin-packing problem[J]. European Journal of Operational Research, 2005, 160(1): 34- 46.

[17] Galinier P, Hertz A. A survey of local search methods for graph coloring[J]. Computers and Operations Research, 2006, 33(9): 2547-2562.

A Heuristic Algorithm for Solving the Bin Packing Problem with Conflicts

YUAN Ye1, LI Yi-jun2

(1.SchoolofManagement,HarbinInstituteofTechnology,Harbin150001,China; 2.DepartmentofManagement,NationalNaturalScienceFoundationofChina,Beijing100085,China)

In real distributions, there are a great many of packing problems with food, medicine and hazardous material named bin packing problem with conflicts, whose objective is to minimize the number of used bins and has to satisfy the conflict constraints among the items. To solve the problems, the mathematical model of BPPC is proposed based on the conflict relationship among the items, packing order and capacity constraints of the bins; and then a heuristic algorithm is designed for solving BPPC, the algorithm computes the maximum clique structure iterately to eliminate the conflict relationship among the items, runs the packing operation according to the items corresponding to the current maximum clique structure, and a local search methed named shuffling strategy is applied to further optimize the current packing results; lastly the simulation experiment is carried out on Iori’s strandard instances compared with the heuristic algorithm based on the graph coloring model, the computational results demonstrate that the heuristic algorithm in this paper is more feasible and effective.

operations research and cybernetics; bin packing problem with conflicts; maximum clique; heuristic algorithm

2013- 07- 02

国家社会科学基金项目资助(10CGL076)；教育部人文社会科学研究青年项目资助(12YJC630160)；黑龙江省自然科学基金项目资助(G201020)；黑龙江省教育厅科学技术研究项目(11551332)

元野(1985-)，男，朝鲜族，博士研究生，主要研究方向：运筹学、物流与车辆调度；李一军(1957-)，男，教授，博士生导师，主要研究方向：管理信息系统、电子商务。

F224.31

A

1007-3221(2015)02- 0051- 07