降低光子晶体谐振腔Q值的方法分析
郝建红 喻 宇
(华北电力大学电气与电子工程学院 北京 102206)
降低光子晶体谐振腔Q值的方法分析
郝建红 喻 宇*
(华北电力大学电气与电子工程学院 北京 102206)
该文在分析计算金属光子晶体的正三角形晶格TE模式的色散特性、全局带隙分布图的基础上,针对金属光子晶体结构谐振腔Q值较高的问题,对降低光子晶体谐振腔Q值的方法进行了分析和设计。采用加载介质柱的混合结构和介质微扰两种方法分别对谐振腔的Q值进行有效的控制,并分析了两种方法对谐振腔模式选择性的影响。结果表明,两种方法都能在不改变谐振腔模式选择性和场分布的基础上有效降低Q值,而介质微扰的方法还同时清除了与TE04竞争的两种杂模,提高了模式选择性。
光子带隙;Q值;谐振腔;模式竞争
1 引言
在毫米、亚毫米和太赫兹波段的回旋器件的注-波互作用过程中,强流电子束间的相互作用强度非常明显,采用基模工作的回旋管由于尺寸小加工困难和热损耗高[1]等问题,往往需要采用过模结构,通过高阶模式[2]进行注-波相互作用。因此,在高功率高频率器件中,比如回旋振荡管,模式竞争就会随着频率的增加而变得更加激烈,使得回旋管的效率变差。为了获得高频纯净模式[3]的微波激励,相互作用结构就必须具有模式选择性。光子带隙[4](Photonic Band Gap, PBG)结构的出现为解决这一问题带来了希望。PBG结构是金属柱[5]或介质柱按空间周期排列构成的,具有频率选择性。跟周期势阱中电子能隙类似,PBG结构[6]中存在电磁波的通带和禁带。当PBG结构中存在缺陷时,频率在禁带[7]内的模式将被束缚在内,频率不在禁带内的模式则会从缺陷中泄漏出去。因此,采用PBG结构可以设计具有频率选择性[8,9]的高频结构。
文献[10]将三角形晶格的光子晶体应用于加速器单元,其工作频率选在17.1 GHz,工作模式为准TM010模。与传统TM010模相比,该光子晶体谐振腔具有以下特点:具有纯净的模式、传统尺寸大小、输入耦合不发生频偏。文献[11]设计并用软件HFSS模拟了PBG回旋振荡管电场分布的结果。该器件工作模式设计为类TE04模,工作频率140 GHz,工作电压68 kV,工作电流5 A,产生25 kW的峰值功率。同年,文献[12]对带有输入耦合的PBG谐振腔进行了理论研究和冷测,工作模式是类TM01模,工作频率是17 GHz。
以往工作研究重点大多集中于PBG回旋管腔的电压、电流、频率以及功率等方面的讨论,而对谐振腔的品质因数Q值则没有予以过多关注。具有较低品质因数的谐振管能最大化地缩小回旋管的自激反应,理论上,一个由PBG结构设计的PBG高频率回旋管的有载Q值[13,14]高达135000,在这个值下回旋管的自激反应非常严重。PBG谐振腔的另一个优势就是它能通过移除一个或多个金属柱从横向有效地提取功率。横向功率[15]提取决定了回旋管的提取效率,然而工作在亚毫米波段的回旋管较长,具有很高的有载Q值,导致有限的提取效率。如果能找到有效的方法控制PBG谐振腔的Q值,那么将不仅能提高PBG谐振腔的提取效率,同时也能解决谐振腔的热损耗的问题。
本文针对金属光子晶体Q值较高的问题,在以上工作的基础上,探讨降低PBG谐振腔Q值的设计方法,以类TE04模为例,分析了采用加载介质柱的混合结构和介质微扰的方法控制PBG谐振腔的Q值大小,并讨论了两种方法对谐振腔模式选择性的影响。
2 基本物理模型分析
由于正三角形阵列缺陷内束缚模式场分布具有更好的角对称性,而且TE模式能更有效地与环形电子注相互作用,本文以TE模式为例加以分析。
由Maxwell方程可以推导出关于位函数的ψ(x⊥)的Helmholtz方程:
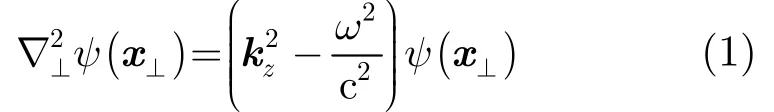
式中,ψ为TE模式的位函数;⊥x为横位移;zk为纵波矢量;ω为角频率;c为光速。
TE模式下金属柱表面满足以下边界条件:

其中n为金属表面的法向量;s为金属表面。
由于电导率在空间上的离散平移对称性,我们可以将Helmholtz方程写成block形式:
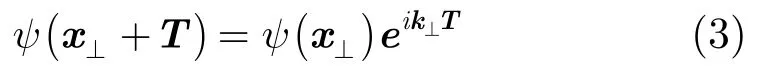
其中,k⊥=kxex+kyey为任意横向波矢量,空间周期矢量T满足:
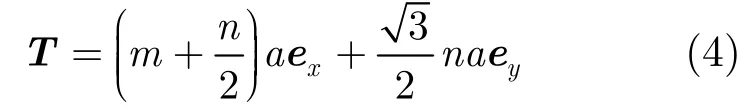
其中m,n为正整数,a为晶格常数。
由式(3)可以导出周期性边界条件:
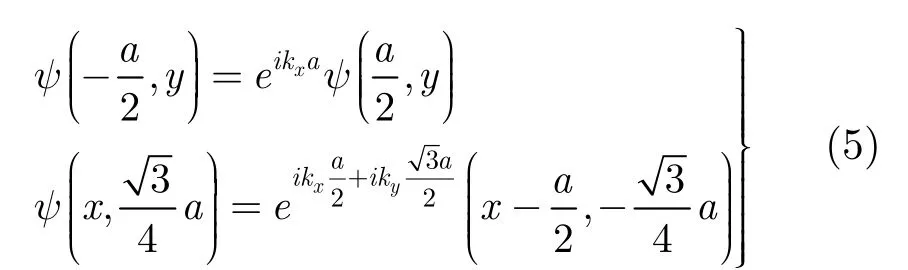
式(1)联立边界条件式(2),式(5)构成了Helmholtz方程的本征问题。
3 PBG谐振腔的电磁模式分析
本文采用有限差分法[16]对Helmholtz方程的本征值问题进行求解,由于正三角形晶格基本单元为菱形,应用有限差分法离散化网格,为充分利用各节点信息,差分格式采用九点差分格式,我们将Helmholtz方程式(1)以及周期性边界条件式(5)分别差分为以下表达式:
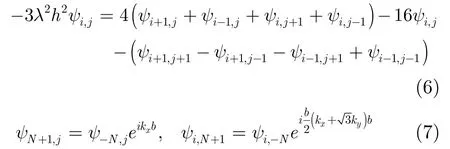
对于式(6)和式(7)的ψi,j方程,将它划分为(2N +1)×(2N+1)=L个网格,就有L个方程,但是除去网格点落在理想导体柱内的M个方程,剩下(LM)个方程,左边构成的矩阵是(L-M)×(L-M)阶矩阵,然后求解特征值,即可得到金属光子晶体全局带隙图。考虑归一化频率ωa/c在0~20, r/a在0~0.5之间变化,其中ω为角频率,r为金属柱半径,a为晶格常数,即金属柱之间的距离。通过数值计算得到TE模全局带隙图,结果如图1所示。
从图1我们可以发现当r/a<0.2时整个PBG结构是不存在全局带隙的,当0.2<r/a<0.33时存在一个全局带隙,而当r/a>0.33时,存在多个全局带隙,图1给出了3个全局带隙分别可以对不同频率的PBG结构进行设计。
图2为金属圆柱正三角晶体的PBG谐振腔截面图,其中R1为中心缺陷的内切圆半径。如图将整个PBG结构中间三层金属柱全部去掉,根据几何关系可以得
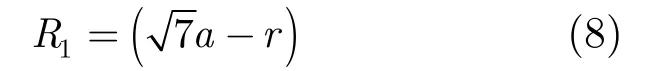
而对于圆柱波导其TEmn模的截止波长满足:

其中ymn为m阶贝塞尔函数的导函数的第n个根,R2为圆柱波导的截止半径。为了方便分析,我们假定PBG结构的内切圆半径与圆柱波导中电磁模式对应的截止半径相近,即
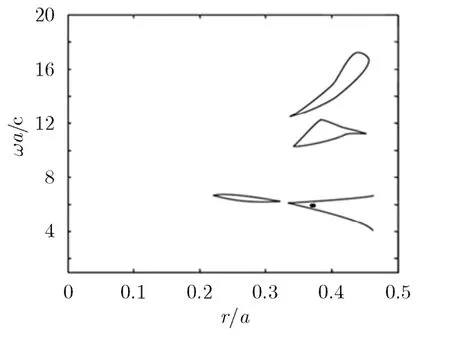
图1 正三角形晶格中TE模式全局带隙图
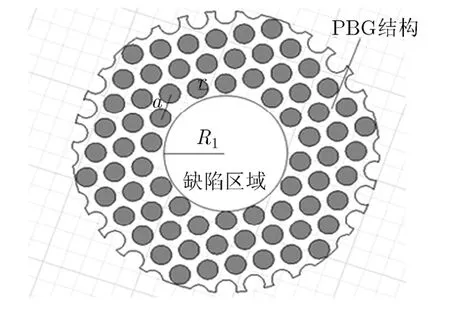
图2 PBG谐振腔截面示意图

因为正三角形结构具有良好的角对称性,因此我们选取角对称性比较好的TE04模来设计PBG谐振腔,选取的工作点如图1(图中的黑点)所示,选择r/a=0.365,晶格常数和金属柱半径分别为a=1.99, r=0.727。图3给出了类TE04模本征频率为141.53 GHz的PBG谐振腔和传统谐振腔横向截面上的场分布图。
对比图3(a)和3(b),可以看出PBG谐振腔有效将TE04模束缚在缺陷区域内,其场分布与普通谐振腔一致且具有一定的模式选择性,但是其Q值却高达13865.2,相比普通141 GHz的普通谐振腔高出10倍之多。
4 降低PBG谐振腔Q值的优化设计
对于谐振频率为140 GHz的PBG谐振腔,它的热负荷和自激反应将非常激烈,严重影响了PBG谐振腔的正常工作。本节将分别讨论采用加载介质柱和介质微扰的方法对PBG谐振腔的Q值进行优化设计,并总结了优化后的PBG谐振腔工作中的工作参数以及竞争模式。
4.1 采用加载介质柱混合结构降低Q值
传统的谐振管直接加载介质柱,电子束会使这些介质充电,这样便会产生额外的空间电荷,导致电子束在传播中发生分裂。目前,一种可以控制PBG回旋管Q值的方法是采用介质柱来代替其中一部分金属柱,形成混合腔。在混合PBG结构中,一方面,为了避免介质填充对谐振腔电磁特性的不良影响,介质柱要尽量远离电子束;另一方面,介质柱置于PBG结构的外层,又削弱了混合结构降低Q值的作用。所以,要综合两方面因素进行介质柱位置的优化设计。
4.1.1 介质柱位置对Q值的影响 在介质柱混合PBG结构中,为了避免介质填充对谐振腔电磁特性的不良影响,在设计上要把介质柱隐蔽在一排或者几排金属柱后面。这样介质柱离电子束通道更远,在介质柱前一排的金属柱将会把电子束屏蔽掉。这种设计能极大减小介质填充的影响。图4分别给出了靠近中心第2层和第3层的铜柱换成介电常数为ε=12.27,介质损耗率为tan(δ)=0.3的介质柱(介质材料陶瓷在真空器件中被广泛应用,在通过低温共烧技术后其介电常数在2~2000范围内变化)后的场分布图,图4(a)结构的品质因数低至135.637,但和图3(b)对比可以看出,这种混合结构的谐振腔虽然大体上把能量禁锢在了缺陷区内,但是边缘区域的能量和电场大小都发生了变化。我们对此进行了改进,将介质柱向外移动一层,如图4(b)所示,计算结果是其Q值为387.676,且电场分布与图3(b)相比没有太大的变化。虽然这种混合结构的PBG腔对于Q值的控制没有图4(a)那么强,但是已经具有很低的有载Q值,能够满足回旋振荡管的加工和工作要求。
为了便于更好地分析介质柱的位置和Q值的关系,我们将谐振腔的周期柱排列扩大到6层,从而进一步分析了第3层和第4层的铜柱加载介质柱对谐振腔Q值的影响,如图5(a)和5(b)所示。为了方便分析,我们将几种位置加载介质柱结构的谐振腔的Q值汇总于表1。由此可知,加载介质柱能够有效的控制Q值的大小,而且随着加载介质柱离中心缺陷区域距离的增加,Q值也随着增加。
实际上,因为此设计采用的是用介质柱的损耗来减少谐振腔的Q值,所以随着介质柱到中心缺陷区域距离的增加,介质柱与中心电子束的作用也跟着降低,Q值也自然升高了。同时我们发现只要介质柱在第3层及其以后其谐振腔的能量和场分布都能比较完善禁锢在中心缺陷区域,所以,为了获得满足要求的场分布和较低Q值的相互作用结构,只要保证最里层为金属柱,设计第3层或其它层为介质柱就可以达到不同程度降低Q值的目的。实际中,可以根据不同的需求进行优化设计,达到最佳状态要求。
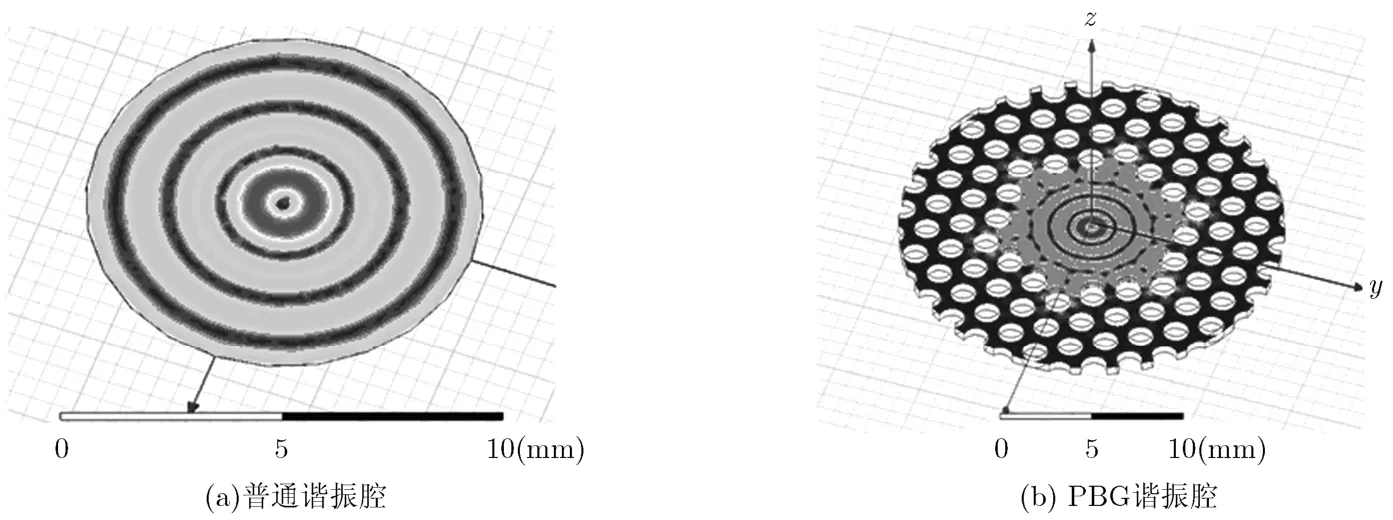
图3 谐振频率为141 GHz的类TE04的场分布
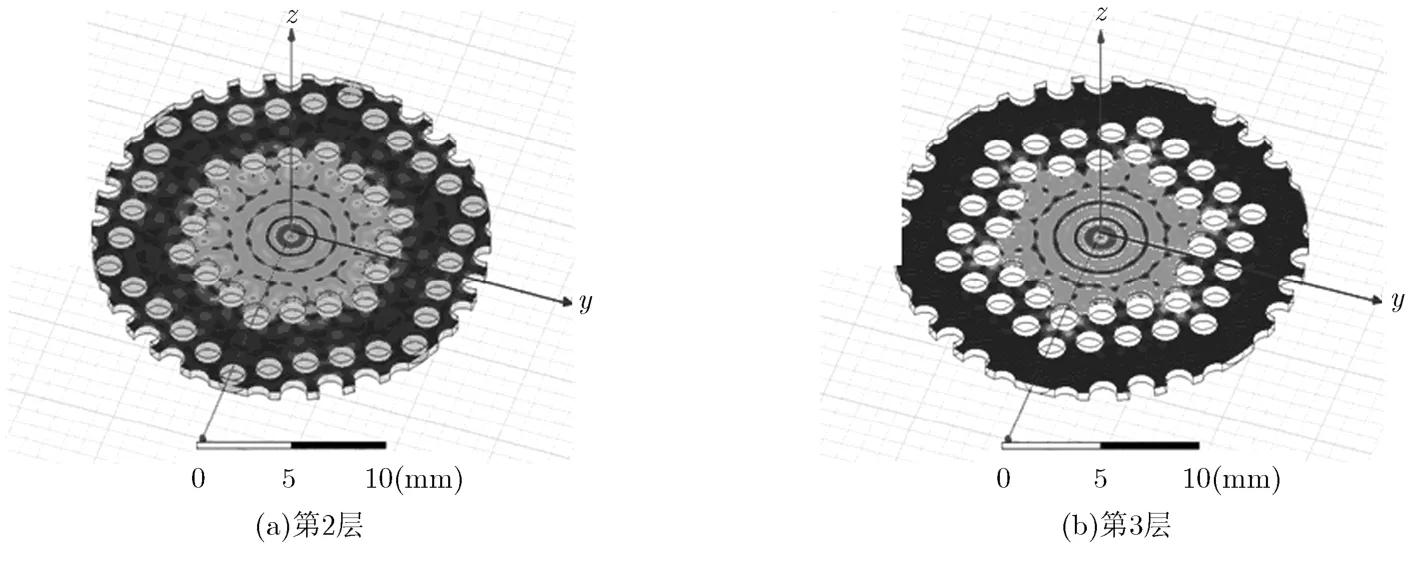
图4 第2层和第3层金属柱换成介质柱后谐振腔的场分布
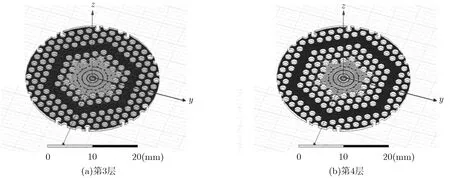
图5 谐振腔第3层和第4层加载介质柱

表1 介质柱的位置和Q值的关系
4.1.2 介质材料对Q值的影响 上一节讨论了介质柱位置变化和品质因数Q的关系,下面将进一步讨论加载介质柱的介电常数和介质损耗率对品质因数Q的影响。保持图4(b)谐振腔结构不变,控制介质损耗率为0.3,可以得出谐振腔Q值随介质柱介电常数的变化,如图6(a)所示,从图中我们可以发现随着介电常数增加品质因数Q值相应增加,基本是呈线性关系,而且变化幅度在100以内,对于一个介质加载谐振腔可以通过调整介电常数的大小对谐振腔Q值进行细微调整。图6(b)也是保持图4(b)谐振腔结构不变,并控制介电常数为12.27时,Q值与介质损耗率的关系,可以看出总体上随着介质损耗率的增加品质因数是减少的,但是随着介质损耗率的增大,介质发热越严重,能量损耗也就越多。在PBG谐振腔中,介质柱是作为一个绝缘体出现在谐振腔内,而当作绝缘材料或电容器材料的高聚物时,介质损耗率越小越好。所以,对于140 GHz的谐振腔介质损耗率最好在0.2~0.3左右。
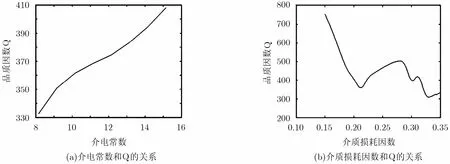
图6 介质材料的参数和Q的关系
以上分析表明,对于加载介质柱的PBG谐振腔,可以根据实际应用需要,用介质柱的位置对谐振腔的Q值进行大调,再用介电常数的大小对谐振腔的Q值进行微调,并同时把介质损耗控制在0.22左右,从而达到满意的要求。
4.2 通过介质微扰控制Q值大小
加载介质柱的混合腔设计虽然在一定程度上可以降低品质因数Q的大小,但同时也造成了一定的介质损耗。考虑到实际工程中,介质柱的损耗是非常严重的,而且介质柱和铜柱之间的距离非常近(大约为0.5 mm),损耗产生的一些污秽物不能及时清理就会附着在铜柱上,对谐振腔电磁特性产生不良影响,影响谐振腔的正常工作。因此为了减小介质损耗对谐振腔电磁特性的影响,我们考虑将加载介质柱设计改为介质微扰的方法来控制Q值的大小。
在由金属柱构成的PBG谐振腔的缺陷区域中,插入4根介质柱作为微扰,插入微扰(介质柱)的位置尽量在TE04场分布为接近为0的位置(见图7(a)),根据文献[17]介质微扰公式为
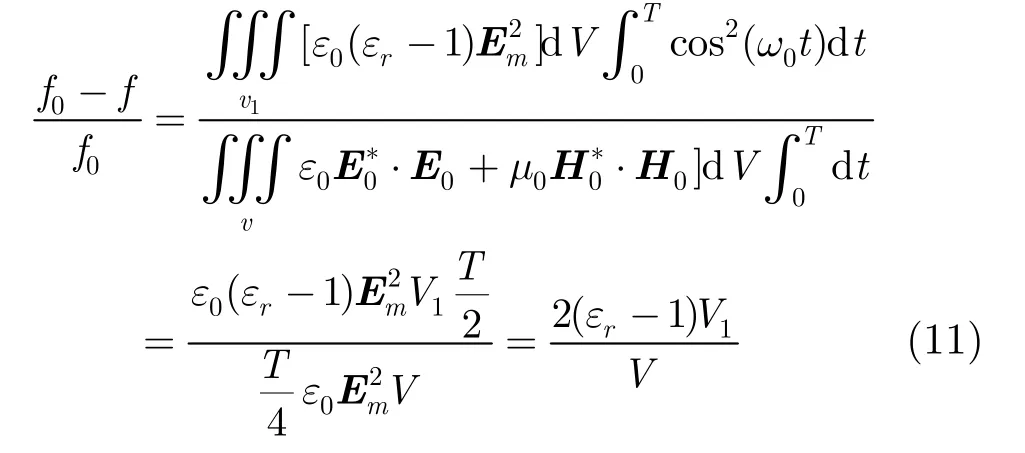
其中f0, f分别表示谐振腔原来的谐振频率和经扰动后的谐振频率,V是谐振腔的体积,V1是加载的介质体积。
式(11)可以计算出谐振腔经微扰后的新谐振频率和材料之间的关系。选定插入圆柱形介质柱的基本参数为:介电常数为11.7,介质损耗为0.22,圆柱半径为0.2 mm,介质柱的高度和腔体高度一致。计算得到介质微扰后的谐振腔的工作频率为142.34 GHz,其Q值为1535.44,与原谐振腔的Q值相比缩小了约9倍,很大程度上控制了Q值的大小。加入介质微扰后谐振腔场分布如图7(b)所示,从图中可以看出,TE04的场分布与未加介质微扰的谐振腔场分布一致,说明介质微扰比介质柱加载对TE04电场的影响要小得多,这主要是因为微扰介质柱放置在TE04模的电场分布为0的位置上,也就是处于图7中圆环部分。从图中我们还可以发现介质柱和铜柱的距离保持在3 mm左右,可以有效地控制介质损耗残留对铜柱的影响。这样不仅保证了谐振腔的工作环境,而且解决了谐振腔Q值过高问题。但这种方法对于谐振腔Q值的控制并没有第1种那么强,而且此种方法略微改变了谐振腔TE04的工作频率,对于工程计算也会带来一些不便。
4.3 低Q值PBG结构谐振腔的模式选择性
PBG谐振腔与普通谐振腔相比最大的优势在于能够很大程度上抑制模式竞争,保证谐振腔的单模运行。对于一个140 GHz的TE04普通谐振腔,在其工作频段上模式竞争非常严重。然而加载PBG结构后的谐振腔能在很大程度上抑制杂模在腔内传播。采用加载介质柱和介质微扰方法能够将PBG谐振腔的Q值进行有效的控制,但不希望破坏它的模式选择性。为此我们在130~155 GHz范围内对普通谐振腔、PBG谐振腔、加载介质的PBG混合腔以及介质微扰的PBG谐振腔进行了模式分布的计算,其结果归纳为表2。
从表2可以看出PBG谐振腔能够有效地减少谐振腔中的竞争模式,加载介质柱的方法并没有影响到PBG谐振腔的模式选择性,而且相应模式的谐振频率也几乎是一样的,所以采用加载介质柱的方法不仅能够有效地控制Q值,而且谐振腔的模式选择性和谐振频率也没有发生改变。另外,采用介质微扰后,谐振腔中存在的模式减少了两种,分别是TE72和TE121,这是因为利用微扰原理改变谐振腔的谐振频率,使原本处于禁带的模式的频率改变,从而将杂模的频率调整到通带频率范围内,增强了谐振腔的模式选择性。所以介质微扰的方法不仅能够有效控制Q值的大小,还能增加谐振腔的模式选择性,但谐振腔的谐振频率略微有所改变。
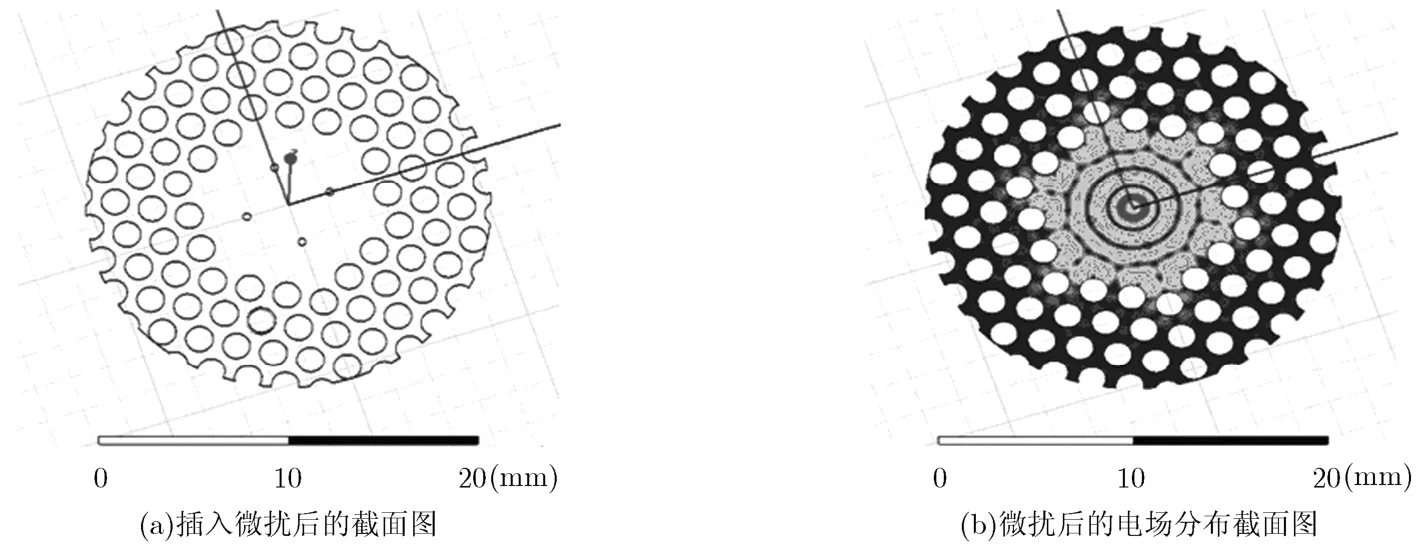
图7 谐振腔的横截面图
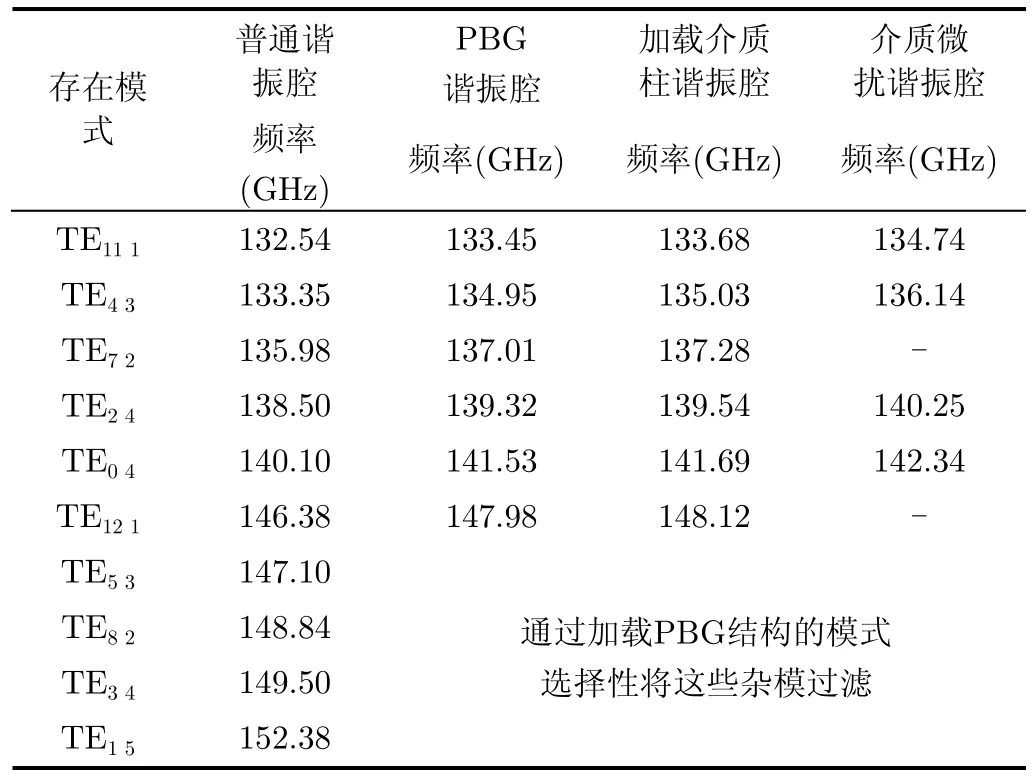
表2 模式选择性的比较
5 结论
本文在分析计算金属光子晶体的正三角形格子TE模式的色散特性、全局带隙分布图的基础上,针对光子金属晶体结构PBG谐振腔Q值较高的问题,设计了两种PBG介质混合结构用于控制PBG谐振腔Q值的大小,两种方法各有利弊,具体总结如下:(1)采用加载介质柱的混合结构能够很大程度上控制PBG谐振腔Q值的大小,并可以通过改变介质柱的位置和介电常数以及介质损耗因数来满足不同工程对Q值的需求。但介质柱损耗残留污秽物会破坏谐振腔的电磁特性,从而影响谐振腔的正常工作。(2)为了减小介质柱对场分布的影响,将介质柱加载改为介质柱微扰,经过微扰后的PBG谐振腔,Q值明显降低,其大小为原PBG谐振腔的1/9,同时也解决了介质残留影响PBG谐振腔电磁特性的问题。(3)比较了两种方法对谐振腔模式选择性的影响,发现加载介质柱的方法并没有改变谐振腔的模式选择性和谐振频率,而介质微扰法不但没有增加谐振腔的模式竞争反而清除了TE04的两种竞争杂模,提高了模式选择性,但会略微提高的谐振腔的谐振频率。
上述降低Q值的方法可以为适合实际需求的PBG谐振腔的工程设计提供理论参考。
[1] John S. Strong localization of photons in certain disordered dielectric super lattices[J]. Physical Review Latters, 1987, 58(23): 2486-2489.
[2] 郝保良, 刘濮鲲, 唐昌建. 二维非正交坐标斜方格金属光子带隙结构[J]. 物理学报, 2006, 55(4): 1862-1867.
Hao Bao-liang, Liu Pu-kun, and Tang Chang-jian. The two-dimensional metal photonic band gap structure consisting of a skew lattice in a nonorthogonal coordinate system[J]. Acta Physica Sinica, 2006, 55(4): 1862-1867.
[3] 闫敦豹, 袁乃昌, 付云起. 基于FDTD的波导介质层PBG结构的研究[J]. 电子与信息学报, 2004, 26(1): 118-123.
Yan Dun-bao, Yuan Nai-chang, and Fu Yun-qi. Research on dielectric layer PBG structures in waveguide based on FDTD[J]. Journal of Electronics & Information Technology, 2004, 26(1): 118-123.
[4] 董玉和, 刘永霞, 朱敏. 速调管输出腔高阶横磁模式加载波导滤波器输出回路[J]. 电子与信息学报, 2013, 35(5): 1267-1270.
Dong Yu-he, Liu Yong-xia, and Zhu Min. Klystron output circuit of high order transverse magnetic mode in coaxial cavityloaded with waveguide filter[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1267-1270.
[5] Yablonovitch E, Gmitter T J, and Leung K M. The facecentered-cubic case employing nonspherical atoms[J]. Physical Review Latters, 1991, 67(17): 2295-2298.
[6] 罗尧天, 唐昌建. 光子带隙谐振腔回旋管振荡器的自洽非线性理论[J]. 物理学报, 2011, 60(1): 014104.
Luo Yao-tian and Tang Chang-jian. Self-consistent nonlinear theory of gyrotron oscillator with photonic-band-gap cavity [J]. Acta Physica Sinica, 2011, 60(1): 014104.
[7] 孙迪敏, 蒋艺, 马国武, 等. 正三角形晶格金属柱光子带隙结构[J]. 强激光与粒子束, 2013, 25(10): 2643-2647.
Sun Di-min, Jiang Yi, Ma Guo-wu, et al.. Metal photonic band gap structures formed by triangular arrays[J]. High Power Laser and Particle Beams, 2013, 25(10): 2643-2647.
[8] 张弛, 罗积润. UC-PBG结构创建准TEM波导的仿真分析[J]. 电子与信息学报, 2010, 32(2): 454-458.
Zhang Chi and Luo Ji-run. Analysis and simulation of the Quasi-TEM waveguide by using UC-PBG structure[J]. Journal of Electronics & Information Technology, 2010, 32(2): 454-458.
[9] 夏玉玺, 刘高峰, 唐昌建. 206 GHz光子带隙谐振腔回旋管[J].强激光与粒子束, 2012, 24(2): 431-435.
Xia Yu-xi, Liu Gao-feng, and Tang Chang-jian. 206 GHz gyrotron with photonic-band-gap cavity[J]. High Power Laser and Particle Beams, 2012, 24(2): 431-435.
[10] Smirnova E I, Kesar A S, Mastovsky I, et al.. Demonstration of a 17 GHz, high-gradient accelerator with a photonic-bandgap structure[J]. Physical Review Latters, 2005, 95: 074801.
[11] Sirigiri J R, Kreischer K E, Macuhzak J, et al.. A photonic band gap resonator gyrotron[J]. Physical Review Latters, 2001, 86(24): 5628-5631.
[12] Smirnova E I, Chen C, Shapiro M A, et al.. Simulationof photonic band gaps in metal rod lattices for microwave applications[J]. Journal of Applied Physics, 2002, 91(3): 960-968.
[13] Sirigiri R. A novel quasioptical gyrotron traveling wave Amplifier[D]. [Master dissertation], Plasma Science and Fusion Center Massachusetts Institute of Technology Cambridge, 2002.
[14] 雷朝军, 喻胜, 李宏福, 等. 94 GHz缓变结构回旋管设计与数值模拟研究[J]. 强激光与粒子束, 2014, 26(2): 3002-3007.
Lei Chao-jun, Yu Sheng, Li Hong-fu, et al.. Design and numerical simulation of a 94 GHz gyrotron with gradually tapered cavity[J]. High Power Laser and Particle Beams, 2014, 26(2): 3002-3007.
[15] 刘畅, 罗尧天, 唐昌建, 等. 回旋管光子带隙谐振腔冷腔电磁模式分析[J]. 物理学报, 2009, 58(12): 8174-8179.
Liu Chang, Luo Yao-tian, Tang Chang-jian, et al.. Electromagnetic mode analysis on the cold characteristics of photonic-band-gap resonant cavity loaded in gyrotron[J]. Acta Physica Sinica, 2009, 58(12): 8174-8179.
[16] 乔海亮, 王玥, 陈再高, 等. 全矢量有限差分法分析任意截面波导模式[J]. 物理学报, 2013, 62(7): 204-207.
Qiao Hai-liang, Wang Yue, Chen Zai-gao, et al.. Full-vectorial finite-difference analysis of modes in waveguide with arbitrary shape[J]. Acta Physica Sinica, 2013, 62(7): 204-207.
[17] 王子宇. 微波技术基础[M]. 北京: 北京大学出版, 2003: 180-184. Wang Zi-yu. Microwave Technology Foundation[M]. Beijing: Peking University Press, 2003: 180-184.
郝建红: 女,1960年生,教授,博士生导师,主要研究方向为高功率微波、混沌控制等.
喻 宇: 男,1989年生,硕士,主要研究方向为高功率微波.
Analysis of the Method to Decrease the Q Value in Photonic Band Gap Cavity
Hao Jian-hong Yu Yu
(Institute of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China)
Based on analyzing the dispersion characteristics and global band gaps for general two-dimensional Photonic Band Gap (PBG) structures formed by triangular arrays of metal posts for TE modes, two methods are proposed to solve the problem of the high Q value in PBG cavity. The result shows that the Q value can be effectively controlled by loading media structures or inserting dielectric perturbation in PBG cavity. In consideration of mode competition in PBG cavity, the mode selection is calculatedrespectively for the two methods. It is shown that the two methods both can control the Q value without reducing the mode selection or changing the electric field distribution of TE04mode. In addition, two competing modes are cleared in the method of dielectric perturbation, which improves the mode selection at the operation frequency of TE04mode.
Photonic Band Gap (PBG); Q value; Resonator; Mode competition
TN129
A
1009-5896(2015)03-0739-07
10.11999/JEIT140486
2014-04-15收到,2014-09-17改回
国家自然科学基金(61372050, 61250008)资助课题
*通信作者:喻宇 252423540@qq.com

