基于I/Q支路相干积分观测滤波的GPS接收机信号跟踪方法

沈 锋 李伟东李 强

(哈尔滨工程大学自动化学院 哈尔滨 150001)

基于I/Q支路相干积分观测滤波的GPS接收机信号跟踪方法

沈 锋 李伟东*李 强

(哈尔滨工程大学自动化学院 哈尔滨 150001)

针对传统GPS接收机在弱信号环境下跟踪误差大，收敛速度慢的缺点，该文提出一种基于I/Q支路相干积分观测滤波的GPS信号跟踪方法。将接收机I/Q支路相干积分输出为观测量，应用无迹卡尔曼滤波(Unscented Kalman Filter, UKF)算法构建卡尔曼滤波器，得到基带数字信号处理滤波模型，闭合接收机跟踪环路。该方法能够有效减小传统GPS跟踪环路中信号参数的估计误差，提高接收机抗干扰能力和弱信号环境下环路跟踪性能。仿真对比结果表明，不同载噪比环境下相比传统GPS信号跟踪的方法，基于I/Q支路相干积分观测的信号跟踪算法能够提高跟踪精度，加快跟踪收敛速度。

全球定位系统；弱信号；跟踪环路；相干积分

1 引言

全球定位系统(GPS)定位误差不随时间积累，全天候提供高精度的定位和导航服务已经实现全球覆盖，在军民领域均具有广阔的用途和发展前景[1,2]。近年来，全球用户对于GPS应用提出了越来越高的要求，应用范围也越来越广泛。

传统GPS接收机在高载噪比(C/N0)强信号环境下跟踪性能良好，但是在弱信号、多路径以及强电磁干扰环境下，接收机跟踪性能受到严重影响，对弱信号处理一直是接收机技术研究的难点[3,4]。针对复杂环境下的GPS信号跟踪问题，文献[5]介绍了用载波跟踪环和码跟踪环结构分别对接收GPS信号中的码相位和多普勒频移进行同步跟踪，确保本地复现信号与输入信号的相关积分值达到最大；文献[6]提出一种位同步方法(K-P法)，能够在低载噪比条件下检测电文数据位边缘，但前提条件是没有载波相位和频率误差；文献[7]利用扩展卡尔曼滤波(Extended Kalman Filter, EKF)消除信号跟踪时的多路径效应，其设计模型较为简单，但不能有效地跟踪微弱信号；文献[8]提出一种将EKF滤波算法和贝叶斯估计结合的方法，实现对弱信号载波和伪码相位的跟踪；文献[9,10]给出了基于自适应卡尔曼滤波的信号跟踪方法，通过历史信息估计噪声协方差矩阵，跟踪变化中的系统模型，由于动态协方差矩阵的非正定性，在微弱信号的环境下容易失锁；文献[11]在分析EKF滤波算法的基础上，将无迹KF(UKF)滤波算法引入到接收机跟踪环路中，完成对载波相位和码相位的估算，但未在弱信号跟踪问题上做深入研究；文献[12]给出了UKF滤波算法在接收机码环中的应用，并通过采用仿真噪声干扰下的微弱GPS伪码中频信号对该算法进行了性能分析，但文中选取的状态量维数低且观测量信息少，未能更好地反应跟踪环路信息。

为解决弱信号环境下的信号跟踪，本文在分析传统GPS接收机载波和码跟踪环路工作的基础上，基于I/Q支路相干积分观测提出了利用卡尔曼滤波器实现GPS信号跟踪方法，该方法利用接收机I/Q支路相干积分输出为观测量，克服传统鉴别器输出时带来的误差，对载波环和码环的特征量进行联合估计并应用UKF滤波构建滤波器模型，通过对非线性函数概率密度函数的估计来获取状态估计，得到基带信号处理滤波模型，能够有效地解决微弱信号下的信号跟踪问题。文中基于UKF滤波算法建立Kalman滤波器模型，采用有限数量的Sigma点集χ对载波频率误差、载波相位误差和码相位误差等参数进行估计，并对不同载噪比环境下的跟踪性能进行了仿真对比分析，验证了所提方法的正确性与有效性。

2 GPS信号跟踪模型

GPS卫星首先利用伪码(C/A码)对数据码进行扩频调制，再将伪码与数据码的组合码通过双相移位键控机制(BPSK)对载波(L1)进行调制。在不考虑噪声的情况下，由接收机天线接收到的第i颗卫星中频信号可写成

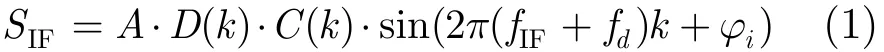
信号跟踪阶段，信号通道从捕获阶段获得的对当前卫星信号载波频率和码相位的粗略估计值出发，通过跟踪环路逐步精细对这两个信号参量的估计[1]。根据鉴别器的不同，载波跟踪环路通常有相位锁定环路(Phase Lock Loop, PLL)和频率锁定环路(Frequency Lock Loop FLL)两种形式，码跟踪环路采用延迟锁定环路(Delay Lock Loop, DLL)。传统的跟踪环路如图1所示。

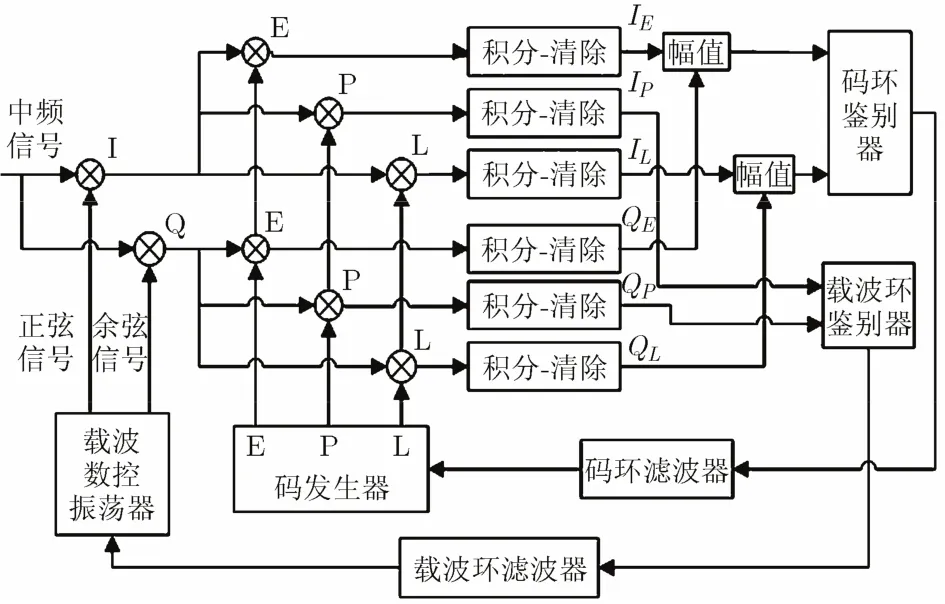
图1 传统GPS跟踪环路总体结构图

在历元k时刻，载波环鉴别器使用即时码(P)相关器的输出值IP和QP，得到载波频率差异δf和相位差异δφ, FLL和PLL分别采用叉积鉴频法和二象限反正切函数鉴相器[13]，载波频率误差和相位误差分别为

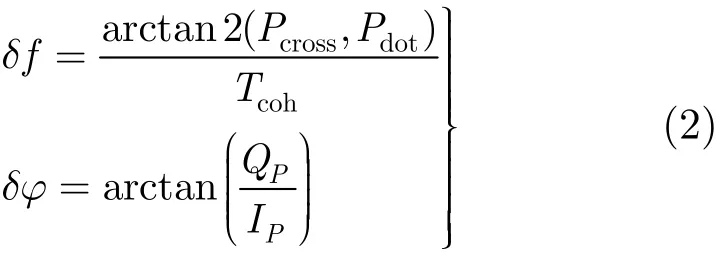
式(2)中，叉积Pcross与点积Pdot分别等于

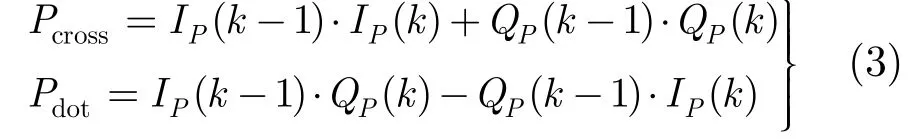
延迟锁定环路(DLL)通过超前码(E)、滞后码(L)相关器的输出来计算码相位误差，采用非相干超前减滞后功率法，码相位误差为

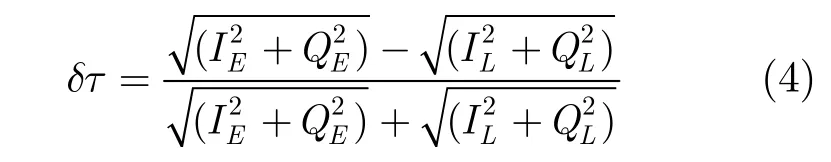
式(4)中，IE,QE,IL和QL为超前支路与滞后支路相干积分值。

环路滤波器通常是一个低通滤波器，其目的在于降低环路中的噪声，载波和码鉴别器的输出经过环路滤波后，将滤波结果反馈给数控振荡器(Numerical Controlling Oscillator, NCO)进而调整本地载波频率、载波相位和伪码相位，载波环路尽力使得本地复现载波信号与卫星载波信号的相位或频率保持一致[2]。码NCO复制出3份不同相位的E、P和L复制C/A码，与接收到的C/A码做相关运算，推算出C/A码自相关函数的主峰位置，从而检测出码相位差异。

在弱信号环境下，传统GPS接收机接收到的信号容易受到内部热噪声和动态应力误差的影响，使GPS接收机跟踪环路中信号参量估计误差加大，且鉴别器在鉴别相位时存在着非线性因素，因此跟踪环路容易产生失锁现象。由于传统跟踪方法处理微弱信号方面的先天性不足，本文提出利用接收机内部跟踪环路I/Q支路相干积分值作为观测量，应用UKF滤波方法构建滤波器模型代替传统算法中载波跟踪和码跟踪的鉴别器。

3 基于I/Q支路相干积分观测信号跟踪算法

3.1 基于相干积分观测滤波的信号跟踪模型

图2为本文所提出的基于I/Q支路相干积分观测滤波的GPS信号跟踪方法，其核心思想是采用Kalman滤波器代替传统GPS跟踪环路中的鉴别器。Kalman滤波是一种利用最小方差准则的最优估计算法，可以对系统状态参量进行精确估计，且可以更为有效地对系统进行控制[14,15]。为了能够准确地跟踪输入信号的频率和相位，选择滤波器状态量为

图2 Kalman滤波器跟踪环路结构图

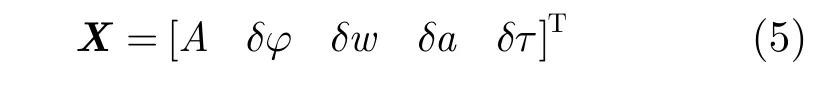
式(5)中，A为归一化信号幅值，δφ为载波相位差，δw 为载波频率差，δa为载波频率变化率，δτ为码相位差。卡尔曼滤波器的状态方程如式(6)所示。

式(6)中，λL为L1载波波长，λCA为C/A码波长， Qk为过程噪声，记为：零均值白噪声序列。

将I/Q支路相干积分输出值作为滤波器的观测量，建立与状态量相关的非线性方程为

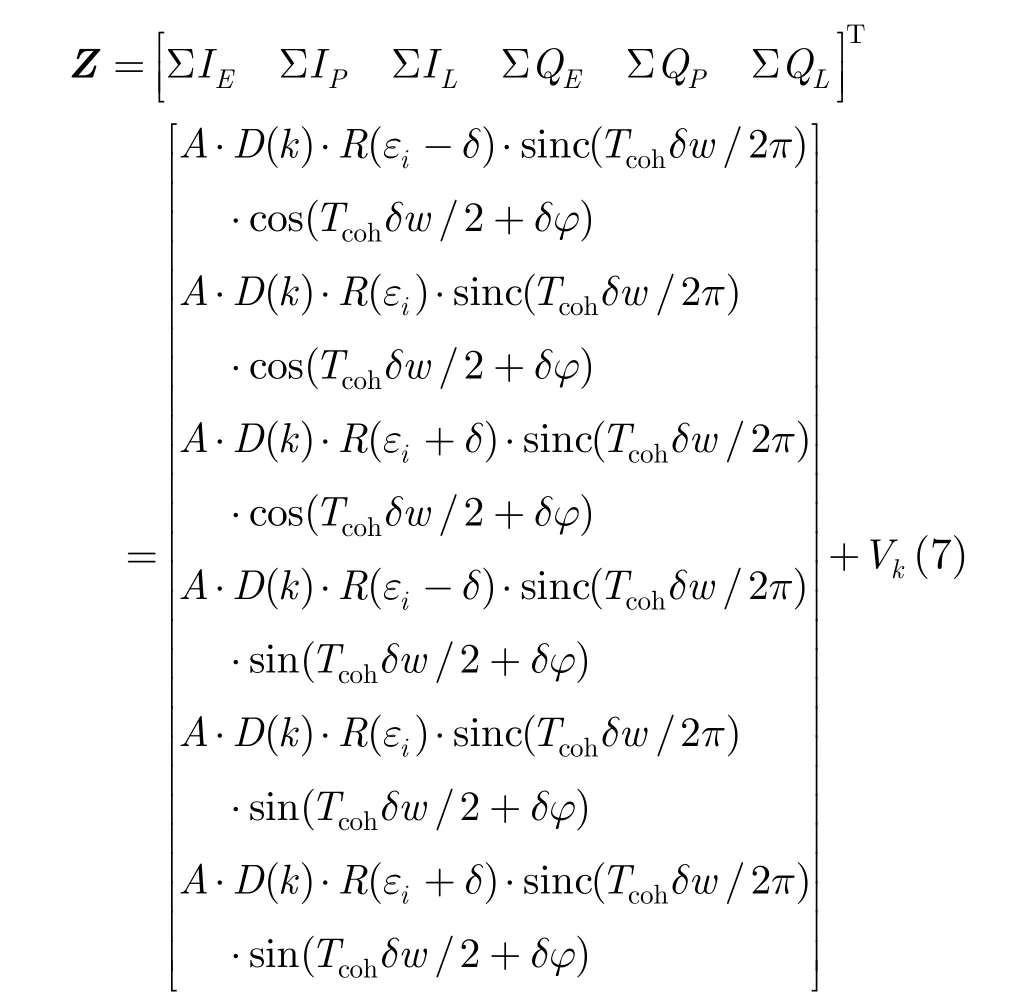
式(7)中，δ为本地C/A码超前滞后间隔，R(εi)为C/A码自相关函数。Vk为量测噪声，噪声方差阵为

式(8)中，σN是相关信号I, Q处理后的噪声强度[11]。跟踪过程中，观测量与状态量存在非线性关系，因此采用UKF滤波算法进行环路滤波处理，得到估计出的载波相位差δφ、载波频率差δw和码相位差δτ。

3.2 基于UKF的卡尔曼滤波器

UKF滤波算法是采用UT变换和传统卡尔曼滤波架构的有效结合，通过对非线性函数概率密度函数的估计来获取状态估计，UT变换是UKF算法的核心和基础。在确保采样均值和协方差为x和px的前提下，选择2n+1个Sigma点集，将非线性变换应用于采样的每个Sigma点，得到非线性转换后的点集和py是变换后Sigma点集的统计量。

卡尔曼滤波器离散化后的非线性系统模型为

状态变量XK初始分布均值为，方差矩阵为P。UT变换产生Sigma点χ和对称采样的加权序列w，表示为

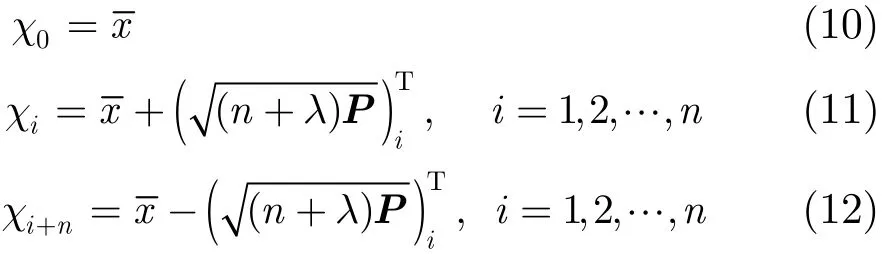
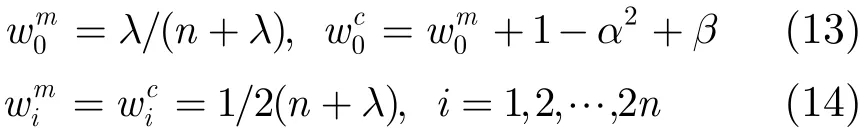
时间更新

测量更新

UKF滤波算法是对非线性函数的概率密度分布进行近似，采用一系列确定的Sigma点集来逼近状态的后验概率密度，避免了EKF滤波算法求导计算雅克比矩阵带来的大量计算，克服了EKF滤波算法线性化忽略高阶项而带来的跟踪精度问题。UKF滤波算法的计算量大小取决于UT变换选择Sigma点集平方根分解运算，当状态变量维数较高时，2n+1个Sigma点增多，UKF滤波算法计算量也会相应地增加，优化平方根分解方式可以减小计算量，同时随着计算机技术的不断发展，计算速度越来越快，滤波算法复杂度带来的滞后问题将会较好地解决。

4 仿真与分析

为了验证基于I/Q支路相干积分值为观测信息的GPS信号跟踪性能与正确性，首先利用传统二阶跟踪环路对GPS中频模拟信号进行跟踪仿真，通过鉴别器输出载波相位差和码相位差。然后利用本文提出的Kalman滤波器模型代替传统的跟踪环路，利用I/Q支路相干积分值为观测量建立系统模型，并输出跟踪信号的误差信息。仿真过程中，数字中频信号频率和采样频率分别设置为1.5 MHz和5 MHz，码速率1.023 Mcps，载波和码环路带宽分别设为8 Hz 和4 Hz，预检测积分时间设为1 ms。

图3为载噪比42 dBHz下的载波相位和码相位跟踪误差对比图，由图可以看出传统二阶跟踪环路在强信号环境下能够较好地跟踪GPS卫星信号，载波跟踪环更新360次左右达到稳态，码环更新580次左右达到稳态，稳态时载波和码环跟踪误差分别控制在10°和0.1个码片内。基于I/Q支路相干积分值为观测量的Kalman滤波模型下的信号跟踪性能更为优越，载波和码跟踪初始阶段均有一个较小的超调量，在环路更新240次左右就能达到稳态值，快速性得到充分体现，且跟踪精度更加准确，能够实时、快速地跟踪接收到的卫星信号。

图4是在32 dBHz下所做的载波相位和码相位跟踪误差对比图，由图可以看出，相对42 dBHz传统二阶跟踪环路信号跟踪性能有所下降，稳态时载波相位和码相位跟踪误差分别扩大到16°和0.2个码片范围内，基于I/Q支路相干积分值为观测量的Kalman滤波模型超调量有所增加，但是其值变化不大。码跟踪环路更新310次左右达到稳态值，较传统二阶码跟踪环路630次更快，快速性仍然能够得到体现，且跟踪精度较传统二阶跟踪环路更高，误差波动范围更小。

表1和表2给出了传统和Kalman滤波模式下跟踪数据对比结果，由表可以看出，载噪比42 dBHz 和32 dBHz环境下，卡尔曼滤波跟踪模式载波和码相位误差的均方差均比传统跟踪模式小，且波动范围较后者要小。在载噪比32 dBHz环境下，传统跟踪模式载波相位均方差9.90°, Kalman滤波模式均方差2.44°，后者要比前者要小很多。传统跟踪模式载波相位误差最大值达到近30°，而Kalman滤波模式最大值仅为6.42°，远小于前者。由此也可以得出，Kalman滤波模式的跟踪性能更优。

图5为传统二阶环路和Kalman滤波器模式在低载噪比24 dBHz下的I/Q支路输出信息对比图，由图5可以看出传统二阶环路在低载噪比环境下，输出的信息是一些发散的数据点，起始阶段跟踪过程就不理想，随着环路鉴别误差逐渐增加，最终导致环路跟踪失锁。而Kalman滤波器模式I支路信息正确解调，Q支路输出的只是一些噪声。Kalman滤波器跟踪模式下系统利用接收机最原始的I/Q支路相干积分值作为观测量，有效减小了使用鉴别器观测时所带来的误差量，在低载噪比环境下仍能正确解调出跟踪的卫星信号导航数据。

图4 传统和Kalman滤波模式载噪 比32 dBHz下跟踪误差对比

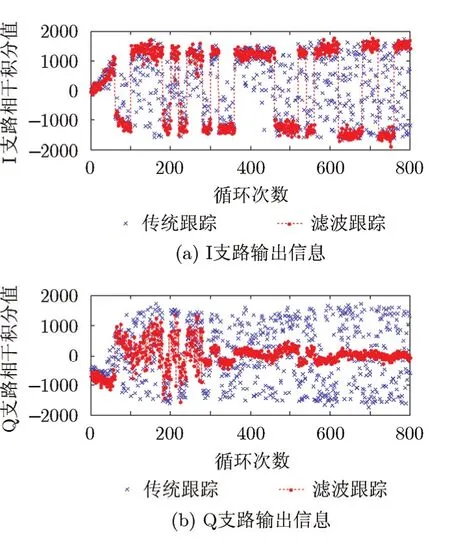
图5 低载噪比下二者I/Q 支路信息对比图

表1 传统和Kalman滤波模式42 dBHz下跟踪数据对比

表2 传统和Kalman滤波模式32 dBHz下跟踪数据对比

为了进一步分析滤波方法的时效性，对传统二阶环路和Kalman滤波器模式的耗时情况进行仿真与分析。

图6为传统二阶环路和Kalman滤波器模式在环路更新过程中的时效性对比图，由图可以看出，跟踪环路更新500次，两者每次环路更新耗时数量级都在毫秒级，时间消耗上差别很小，在滤波器中引入UKF滤波算法，不但在跟踪性能上得到改善，而且算法复杂度引起的时间滞后问题也随着计算机技术的发展而得到改善。

5 结束语

图6 传统和Kalman滤波模式下时效性对比

在对传统跟踪环路通过鉴别器输出误差信息分析的基础上，提出基于I/Q支路相干积分观测的Kalman滤波模型及应用UKF滤波算法进行仿真。通过Kalman滤波处理与传统跟踪环路在不同载噪比环境下的性能仿真对比，可以得出：应用UKF滤波算法处理非线性信号快速收敛、对动态参量能够精确估计，使其具有更高的跟踪精度，更快的收敛速度，在低载噪比的环境下能够较好地跟踪卫星信号，正确地解调出卫星信号中的数据码信息，比传统跟踪环路在弱信号环境下具有更为优越的跟踪性能。

[1] 田甜, 安建平, 王爱华. 高动态环境下无数据辅助的扩展Kalman滤波载波跟踪环[J]. 电子与信息学报, 2013, 35(1): 63-67. Tian Tian, An Jian-ping, and Wang Ai-hua. Non-data-aided extended Kalman filter based carrier tracking loop in high dynamic environment[J]. Journal of Electronics & Information Technology, 2013, 35(1): 63-67.

[2] 谢钢. GPS原理和接收机设计[M]. 北京: 电子工业出版社,2009: 1-2.

[3] Lashley M, Bevly D M, and Hung J Y. Performance analysis of vector tracking algorithms for weak GPS signals in high dynamics[J]. IEEE Journal of Selected Topics in Signal Processing, 2009, 3(4): 661-673.

[4] 赵琳, 丁继成, 孙明, 等. 极弱信号环境下GPS位同步和载波跟踪技术[J]. 航空学报, 2010, 31(6): 1205-1212. Zhao Lin, Ding Ji-cheng, Sun Ming, et al.. Bit synchronization and carrier tracking for very weak GPS signals[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(6): 1205-1212.

[5] Wu Ling-juan and Cui Ying-ying. Signal acquisition and tracking for software GPS receivers[C]. Proceedings of the Asia Pacific Conference on Postgraduate Research in Microelectronics & Electronics, Shanghai, China, 2009: 384-387.

[6] Kokkonen M and Pietila S. A new bit synchronization method for a GPS receiver[C]. Proceedings of the IEEE Position Location and Navigation Symposium, Palm Springs, CA, 2002: 85-90.

[7] Jee G, Kim H S, and Lee Y J. A GPS C/A code tracking loop based on extended Kalman filter with multipath mitigation [C]. Proceedings of the Institute of Navigation GPS, Portland, USA, 2002: 446-451.

[8] Psiaki M L and Jung H. Extended Kalman filter methods for tracking weak GPS signals[C]. Proceedings of the Institute of Navigation GPS 2002, Portland, 2002: 2539-2553.

[9] E Shi. An improved real-time adaptive Kalman filter for low-cost integrated GPS/INS navigation[C]. Proceedings of the 2012 International Conference on Measurement, Information and Control (MIC), Harbin, China, 2012: 1093-1098.

[10] Janos G and Andrei C. A simplified adaptive Kalman filter algorithm for carrier recovery of M-QAM signals[C]. Proceedings of the 17th International Conference on Methods and Models in Automation and Robotics (MMAR), Szczecin, Poland, 2012: 303-307.

[11] 张敏虎, 任章, 华春红. UKF在深组合GPS/INS导航系统中的应用[J]. 中国惯性技术学报, 2009, 17(6): 697-700. Zhang Min-hu, Ren Zhang, and Hua Chun-hong. Application of UKF in deeply coupled GPS/INS navigation system[J]. Journal of Chinese Inertial Technology, 2009, 17(6): 697-700.

[12] 曾庆喜, 唐琳琳, 王庆, 等. 基于UKF的GPS L1 C/A码微弱信号跟踪算法[J]. 舰船电子工程, 2014, 35(1): 58-62. Zeng Qing-xi, Tang Lin-lin, Wang Qing, et al.. Weak signal tracking algorithm base on UKF for L1 C/A code[J]. Ship Electronic Engineering, 2014, 35(1): 58-62.

[13] Li Hui and Yang Jing-shu. Analysis and simulation of vector tracking algorithms for weak GPS signals[C]. Proceedings of the International Asia Conference on Informatics in Control, Automation and Robotics, Hefei, China, 2010: 215-218.

[14] Luo Yong, Ravindra Babu, Wu Wen-qi, et al.. Double-filter model with modified Kalman filter for baseband signal pre-processing with application to ultra-tight GPS/INS integration[J]. GPS Solutions, 2012, 16(4): 463-476.

[15] 谢非, 刘建业, 李荣冰, 等. 基于环路相关积分观测的SINS/ GPS 深组合导航算法[J]. 中国惯性技术学报, 2013, 21(4): 472-477. Xie Fei, Liu Jian-ye, Li Rong-bing, et al.. Deeply SINS/GPS integrated navigation algorithm based on tracking loop correlation measurements[J]. Journal of Chinese Inertial Technology, 2013, 21(4): 472-477.

[16] 王璐, 李光春, 乔相伟, 等. 基于极大似然准则和最大期望算法的自适应UKF算法[J]. 自动化学报, 2012, 38(7): 1200-1210. Wang Lu, Li Guang-chun, Qiao Xiang-wei, et al.. An adaptive UKF algorithm based on maximum likelihood principle and expectation maximization algorithm[J]. Acta Automatica Sinica, 2012, 38(7): 1200-1210.

沈 锋： 男，1981年生，副教授，研究方向为信号检测、卫星导航技术研究.

李伟东： 男，1989年生，硕士生，研究方向为卫星导航技术研究、SINS/GPS深组合导航.

李 强： 男，1987年生，博士，研究方向为卫星导航、GPS/INS组合导航.

GPS Receiver Signal Tracking Method Based on I/Q Branch Coherent Integration Measurements Filter

Shen Feng Li Wei-dong Li Qiang
(College of Automation, Harbin Engineering University, Harbin 150001, China)

Due to the disadvantages of a traditional GPS receiver in the environment of weak signal are that slow convergence rate and serious tracking error, a GPS signal tracking algorithm is proposed, in which the coherent integration of I/Q branch is considered as measurement of Unscented Kalman Filter (UKF). The filter model of the baseband signal processing is constructed and tracking loop is closed by UKF. Then the signal parameters of GPS tracking loop can be accurately estimated. Moreover, the anti-jamming capability and tracking ability of receiver are improved in the presence of weak signals. Simulation results demonstrate that the tracking ability and convergence rate of proposed algorithm outperform traditional method in the case of different Carrier to Noise ratio (C/N).

GPS; Weak signal; Tracking loop; Coherent integration

TN966

A

1009-5896(2015)01-0037-06

10.11999/JEIT140314

2014-03-10收到，2014-06-23改回

国家自然科学基金(61102107, 61374208)和中央高校基本科研业务费专项基金(HEUCFX41310)资助课题

*通信作者：李伟东 lwd52531258@163.com