遗传算法在城轨运行图优化中的应用
李皓宇,陈荣武,林 蓝
(西南交通大学 信息科学与技术学院, 成都 610031)
遗传算法在城轨运行图优化中的应用
李皓宇,陈荣武,林 蓝
(西南交通大学 信息科学与技术学院, 成都 610031)
随着城市轨道交通的迅猛发展,如何在现有基础设施的情况下最大限度地提高运输效率、提升运输能力是城市轨道交通运营中一个迫切需要解决的问题。本文旨在通过建立运行图优化模型,利用遗传算法对其进行优化的方式来优化运行图运营组织过程,从而达到提高运输效率、提升运输能力的目的。
城市轨道交通;运行图;遗传算法
我国城市轨道交通在近几年内飞速发展,一线城市如北京、上海等,已形成较为完善的城市轨道交通运输网,涵盖城市范围广,成都、武汉、重庆等城市已建成地铁线路或正在规划建设中。如何提高城市轨道交通运输效率成为城轨运营组织中一个有待解决的关键课题。
列车运行图是城市轨道交通运输组织的重要组成部分,城市轨道交通运行图算法优化研究与实现更是提高运行图质量的基础。因此,研究一个高效、准确的运行图优化算法对于城市轨道交通运输系统显得尤为重要。本文采用遗传算法,对城市轨道交通运行图进行建模,确立优化目标,对运行图中各项时间数据进行优化,从而达到提高城轨运输能力、运输效率的目的。
1 城市轨道交通运行图概述
列车运行图作为铁路列车运营的关键技术文件,规定了列车在铁路区间的运行时分,列车在各个车站的到发时刻以及在车站的停站时间等,是铁路组织列车运行的基础。城市轨道交通运行图通常以横坐标表示时间,纵坐标表示距离的方式来显示。
根据不同使用需求,列车运行图按时间划分有3种:二分格形式、十分格形式和小时格形式。由于城市轨道交通时隔短、距离短等因素,实际应用中常使用二分格运行图。二分格运行图如图1所示,它的横轴是以间隔2 min的细竖线加以划分,10 min线和小时线均用较粗的竖线表示[1]。

图1 城市轨道交通运行图
在城市轨道交通中,列车运行图由一些必要的基本要素组成,包括:列车在相邻两车站之间的运行时分;列车在每个车站的停站时间(由列车在每个车站的到发时刻确定);追踪列车间隔时间等。对列车运行图进行优化的过程,也就是对这些要素进行优化的具体过程。
2 运行图优化问题
如前文所述,列车运行图主要影响因素有两点:列车在站间的运行时分以及列车在车站的停站时间。那么对运行图的优化问题就可以简化为对这两项参数的优化问题了,同时还需要考虑系统列车追踪间隔时间的限制条件[2]。
列车区间运行时分取决于两站间的线路距离和列车运行速度。当列车在区间以最大的允许速度移动时,列车在站间运行时分最小。然而列车运营要考虑效率和节能要求,并且要给乘客营造一个舒服的乘车环境,就需要限制列车站间运行的最大时间,在这个最大和最小运行时分之间,就是我们能对列车的运行时分进行变动的范围。

列车最小停站时分是通过列车到站后,司机开关门的操作时间及乘客上下车时间两方面来决定的。车站不一样,客流多少也不一样,所以停站最小时间值也会由于在不同车站而略有不同。同样,列车在站内的停车时间不能无限地拉长(考虑到行车追踪间隔等因素),所以停站时分最大值也必须规定好。
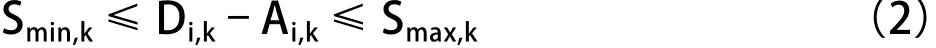
本文中,运行图优化问题归结为一个最终目标:在适当的范围内,最小化总旅行时间。由前文描述可知,运行图有两个主要的可优化参数:区间运行时分和车站停站时分。我们可以对这两个目标进行适当优化,达到最小化总旅行时间的目的。
3 模型及算法
在建立列车运行优化模型的过程中,主要分为两个步骤:
(1)确定优化目标;(2)根据运行图的各种约束条件,利用遗传算法对优化目标进行优化。
3.1 算法概述
本文采用遗传算法对优化模型进行仿真验证,遗传算法的灵感来源于人类自然进化的过程。人的进化过程通过染色体的选择、交叉以及变异过程实现,染色体的选择、变异和重组过程都是无记忆的。将这些概念用数学方法进行表述就形成了遗传算法的基本机理[3]。其基本原理如图2所示。

图2 遗传算法流程图
(1)编码:把待解决问题的数据信息用遗传算法的方式表示出来,它是运用遗传算法求解问题的第1步。
(2)选择:在群体中选择适应度高的个体产生新的个体的过程。遗传算法采用选择算子来对群体中的个体进行优胜劣汰的操作,选择适应度高的个体产生新个体直到求得最优解。
(3)交叉:又称重组,它模仿了染色体基因互换的过程。按一定的概率从个体中选择两个个体,对这两个个体的编码染色体交叉位置进行确定,确定交叉位置后进行交叉。交叉在遗传算法过程中起关键作用,在编码设计时要一起考虑。
(4)变异:就是以较小的概率对个体染色体编码上的某些位置进行突变操作,如二进制编码中“0”变成“1”和“1”变成“0”,进而产生新个体编码,它能够避免由于选择和交叉运算而造成的某些信息丢失,保证遗传算法的有效性。
(5)适应度函数:适应度函数的设计种类可以有很多,一般需要满足单值、连续、非负、一致性好并且计算量小等要求。
(6)约束条件处理:对约束条件进行处理是遗传算法中必须进行的,需要具体问题具体分析。针对具体问题选择合适的约束条件处理方法,是求解问题的重要一步。
(7)控制参数选择:遗传算法中控制参数选择至关重要,这些控制参数包含群体规模N,编码长度L,交叉概率,变异概率等。一般建议取值范围是0.2~0.99,的取值范围是0.001~0.1。
3.2 建模与仿真
3.2.1 模型的建立
(1)确定目标函数
目标函数是列车运行图优化模型建立的第一步,它和城市列车运行图优化的目标直接相关,为了确定模型的目标函数,可以通过分析待优化目标的方式来进行。通常,在城市轨道交通运行图优化问题中,我们可以简化地以最小化全旅行时间作为优化目标,计划的总旅行时间由第i列车在每一站的停站时间和两两站间的运行时分之和组成[4]。
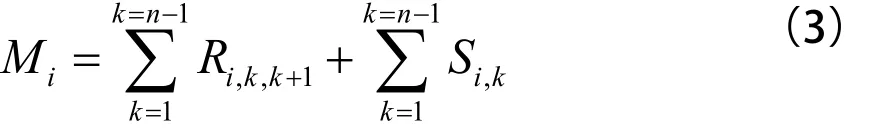
因此对第i列车的优化目标函数F(i)为:

(2)确定约束条件
一般来说,在城市轨道交通的运行图优化问题中,约束条件有以下几种:用户约束、运营约束、铁路基础设备约束等。本文里,只考虑用户约束、运营约束和列车追踪间隔时间约束。
a.用户约束:列车在起点站的发车时间约束和在终点站的到达时间约束。
b.运营约束:列车区间的运行时分约束和列车在车站的停站时间约束。

c.列车追踪间隔时间的约束:为保证两列车间的安全运行,其追踪间隔时间要在安全运行允许的范围内变化[5]。
3.2.2 仿真
本文选取北京1号线八通段进行仿真验证。根据北京地铁官方网站2014年所公布的信息,车站数据与列车站间运行时间数据如表1、表2和表3所示。

表1 车站数据

表2 站间距离及运行时分

表3 时刻表数据
其中,表2中的运行时分由运行等级确定,运行等级分为1、2、3、4级,分别表示最高时速(80 km/h)的100%、90%、75%和50%。
利用遗传算法对以上基础数据进行二进制编码,计算目标函数、适应度函数,通过选择交叉变异对目标函数进行优化,输出优化后的时间数据。并通过运行图软件界面显示出优化后的线路数据,结果如表4所示。
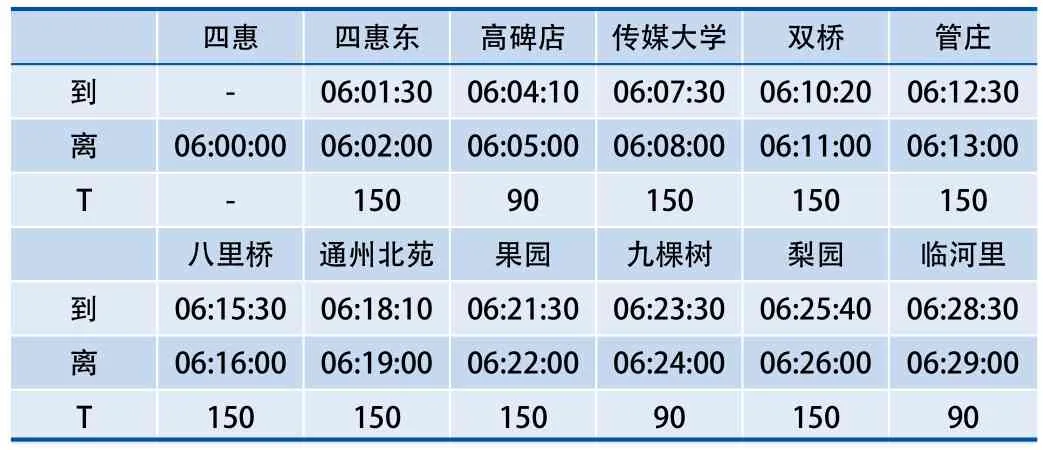
表4 优化后的运行数据
对比表3和表4的数据,总旅行时间从30 min减小到29 min,达到了对总旅行时间的优化目的。具体看来,路线中列车在四惠东、高碑店、双桥等站的到站时间发生了改变,在高碑店、通州北苑等站的停站时间发生了改变。利用运行图显示界面对优化后的数据进行显示,如图3所示。
综上,优化前后列车的总旅行时间减少了1 min,达到了优化总旅行时间的目的,验证了算法的有效性。
4 结束语
城轨运行图优化问题是一个多约束多目标的优化问题。本文中,为了简化优化模型,将目标设为最小化全旅行时间,以到发时间为变量,采用遗传算法对问题进行求解。在实验室平台下,通过运行图显示界面对优化结果进行了验证,结果表明,该算法有效,能够达到优化运行图的目的。
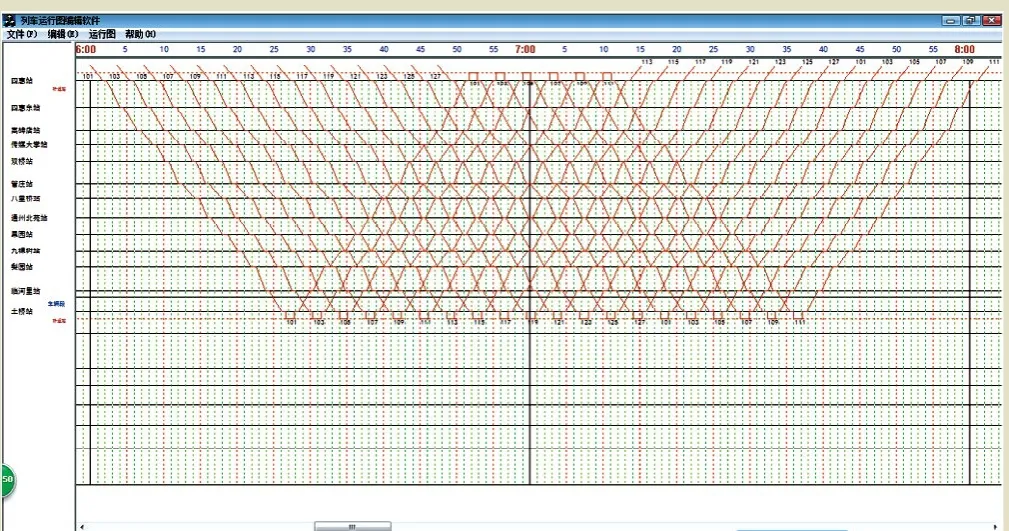
图3 运行图显示界面
[1]胡思继. 铁路行车组织[M]. 北京:中国铁道出版社, 2009:174-178.
[2]陈荣武, 诸昌钤, 刘 莉. CBTC 系统列车追踪间隔计算及优化[J]. 西南交通大学学报, 2011, 46(4):579-582.
[3]张文修,梁 怡. 遗传算法的数学基础[M]. 西安:西安交通大学出版社, 1999.
[4]章优仕, 金炜东. 基于遗传算法的单线列车运行调整体系[J].西南交通大学学报, 2005, 40(2):147-152.
[5]陈国良.遗传算法及其应用[M].北京:北京邮电出版社,1996.
责任编辑 王 浩
Optimization of Urban Transit diagram based on Genetic Algorithm
LI Haoyu, CHEN Rongwu, LIN Lan
( School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, China )
With the rapid development of Urban Transit, how to improve the transportation eff i ciency and capacity with existing infrastructures has become a urgent problem to be solved. We established a running optimization model by using Genetic Algorithm in order to improve the transportation eff i ciency and capacity of Urban Transit.
Urban Transit; diagram; Genetic Algorithm
U231.92∶TP39
A
1005-8451(2015)12-0059-04
2015-03-11
李皓宇,在读硕士研究生; 陈荣武,高级工程师。

